
Exercices : les Logarithmes Népériens
Dans quelles circonstances peut-on utiliser la fonction logarithme changeant produit en somme ? La fonction logarithme qui change produit en somme est une démarche qui implique d'utiliser des logarithmes en base ?, appelés logarithmes népériens. On se sert de ces derniers pour transformer des produits en sommes de logarithmes, tout simplement ! Ainsi, lorsque vous[…]
23 avril 2024 ∙ 12 minutes de lecture

Les Propriétés de la Fonction Exponentielle
Comment définir et utiliser la fonction exponentielle ? Celui qui croit à une croissance exponentielle infinie dans un monde fini est soit un fou, soit un économiste. Kenneth Boulding Dans le programme de Terminale, la fonction exponentielle est une notion qui s'impose comme un outil mathématique dont les contours sont parfois complexes à saisir. Pourtant,[…]
12 octobre 2023 ∙ 4 minutes de lecture

La Fonction Exponentielle
Que faut-il savoir sur la fonction exponentielle ? La fonction exponentielle est une fonction mathématique fondamentale exprimée par f(x) = e^x, où "e" est une constante approximativement égale à 2.71828. Cette fonction présente une croissance rapide et continue avec l'augmentation de "x". ? Elle est utilisée pour modéliser des phénomènes de croissance exponentielle dans divers[…]
29 juillet 2023 ∙ 4 minutes de lecture

Limites et Formes Indéterminées
Comment lever une forme indéterminée ? En mathématiques, une levée de fonction d'une forme indéterminée fait référence à une méthode utilisée pour déterminer la limite d'une fonction lorsque son expression est de type indéterminé, c'est-à-dire lorsqu'il est impossible de l'évaluer directement. ? Cette méthode consiste à transformer l'expression indéterminée en une forme équivalente qui permet[…]
26 juin 2023 ∙ 4 minutes de lecture

Exercice de Probabilité avec boules et le corrigé
Comment étudier les espaces probabilisés ? Introduction Dans votre scolarité a été introduit le concept d'espace probabilisé dans le contexte d'un univers complet. Nous allons ici généraliser les définitions à n'importe quel univers tout en nous concentrant sur le cas où l'univers n'est pas complet. La théorie est plus compliquée : un événement ne doit[…]
7 avril 2022 ∙ 11 minutes de lecture

Terminale – Suites : Récurrence III
Terminale – Les suites : La récurrence III Voici un cours pratique sur les suites réalisé par des ambassadeurs Superprof qui ont lancé leur application de e-learning, Studeo : preview exclusive pour Superprof ! Il se décompose en deux temps : une vidéo de cours de 5 minutes pour comprendre les points clés, un exercice d'application[…]
10 mars 2022 ∙ 1 minute de lecture

Terminale – Fonctions : Théorèmes de Convergence
Terminale – Fonctions : Théorèmes de Convergence Voici un cours pratique sur les fonctions réalisé par des ambassadeurs Superprof qui ont lancé leur application de e-learning, Studeo : preview exclusive pour Superprof ! Il se décompose en deux temps : une vidéo de cours de 5 minutes pour comprendre les points clés, un exercice d'application et[…]
27 janvier 2022 ∙ 2 minutes de lecture

Terminale – Trigonométrie 3/3 : inéquations trigos (PDF inclus !)
Terminale – Trigonométrie 3/3 : inéquations trigonométriques (PDF inclus !) Voici un cours pratique sur les inéquations trigonométriques réalisé par des ambassadeurs Superprof qui ont lancé leur application de e-learning, Studeo : preview exclusive pour Superprof ! Il se décompose en deux temps : une vidéo de cours de 5 minutes pour comprendre les points[…]
16 août 2021 ∙ 1 minute de lecture

Terminale – Trigonométrie 2/3 : équations trigos (PDF inclus !)
Terminale - Trigonométrie 2/3 : équations trigonométriques (PDF inclus !) En terminale spécialité mathématiques, les élèves vont aborder la trigonométrie sous un nouvel angle : celui des fonctions. Voici un cours pratique sur la résolution des équations trigonométriques réalisé par des ambassadeurs Superprof qui ont lancé leur application de e-learning, Studeo : preview exclusive pour[…]
16 août 2021 ∙ 1 minute de lecture

Terminale – Trigonométrie 1/3 : la dérivabilité en vidéo (PDF inclus !)
Terminale - Trigonométrie 1/3 : comprendre la dérivabilité en vidéo (PDF inclus !) En terminale spécialité mathématiques, les élèves vont aborder la trigonométrie sous un nouvel angle : celui des fonctions. Voici un cours pratique sur la dérivabilité des fonctions trigonométriques réalisé par des ambassadeurs Superprof qui ont lancé leur application de e-learning, Studeo :[…]
16 août 2021 ∙ 2 minutes de lecture

La Récurrence et les Limites de suite
Qu'est ce que le raisonnement par récurrence et la limite d'une suite ? Introduction Les suites permettent de traduire beaucoup de situations connues dans la vie de tous les jours. Elles sont utiles dans beaucoup de domaines autres que les mathématiques. Il est important de savoir les étudier, par exemple de connaître sa limite, mais[…]
8 mars 2021 ∙ 8 minutes de lecture

Fonctions usuelles
Quelles sont les différentes fonctions utilisées en mathématiques ? Introduction On étudie ici les fonctions réelles à une variable réelle. Cela signifie qu'on définit une application f qui a toute inconnue x associe le nombre f(x). Différentes fonctions existes et sont très utilisées en mathématique comme en physique : les fonctions affines, la fonction carré,[…]
14 janvier 2021 ∙ 6 minutes de lecture

Arithmétique : divisibilité et PGCD
Comment étudier la divisibilité, les nombres premiers et le PGCD ? Introduction Division euclidienne, PGCD, trop facile ? Et bien non. Derrière des notions simples se cachent en faite des théorèmes bien plus compliqués. Théorème de Gauss, de Bezout et algorithme d'Euclide, regardons tout ce que le monde des mathématiques peut nous faire découvrir. La[…]
24 juin 2019 ∙ 8 minutes de lecture

Etude de Fonction
Comment étudier la parité, le signe, les limites et les variations d'une fonction ? Introduction Comme la courbe de croissance d'un enfant en fonction de son age ou encore la courbe d'IMC en fonction du poids et de la taille, beaucoup de choses qui nous entoure peuvent être exprimées sous forme de fonctions. Les fonctions[…]
12 juin 2019 ∙ 7 minutes de lecture

La Récurrence
Qu'est ce que le raisonnement par récurrence ? Introduction En mathématiques, il existe différentes méthodes pour démontrer une proposition ou une propriété. La récurrence est l'une d'entre elles. C'est une méthode simple qui permet de démontrer une assertion sur l'ensemble des entiers naturels. Définition La première question que l'on se pose est bien-sur : à[…]
6 juin 2019 ∙ 5 minutes de lecture

Les Limites de Fonction
Qu'est ce que la limite d'une fonction et comment la déterminer ? Introduction Une fonction numérique est un procédé mathématique qui associe à tout nombre x un unique nombre y. Pour comprendre une fonction, on étudie son signe, ses variations, ainsi que ses limites ! Définitions et théorèmes Définitions La limite de la fonction f[…]
3 juin 2019 ∙ 4 minutes de lecture
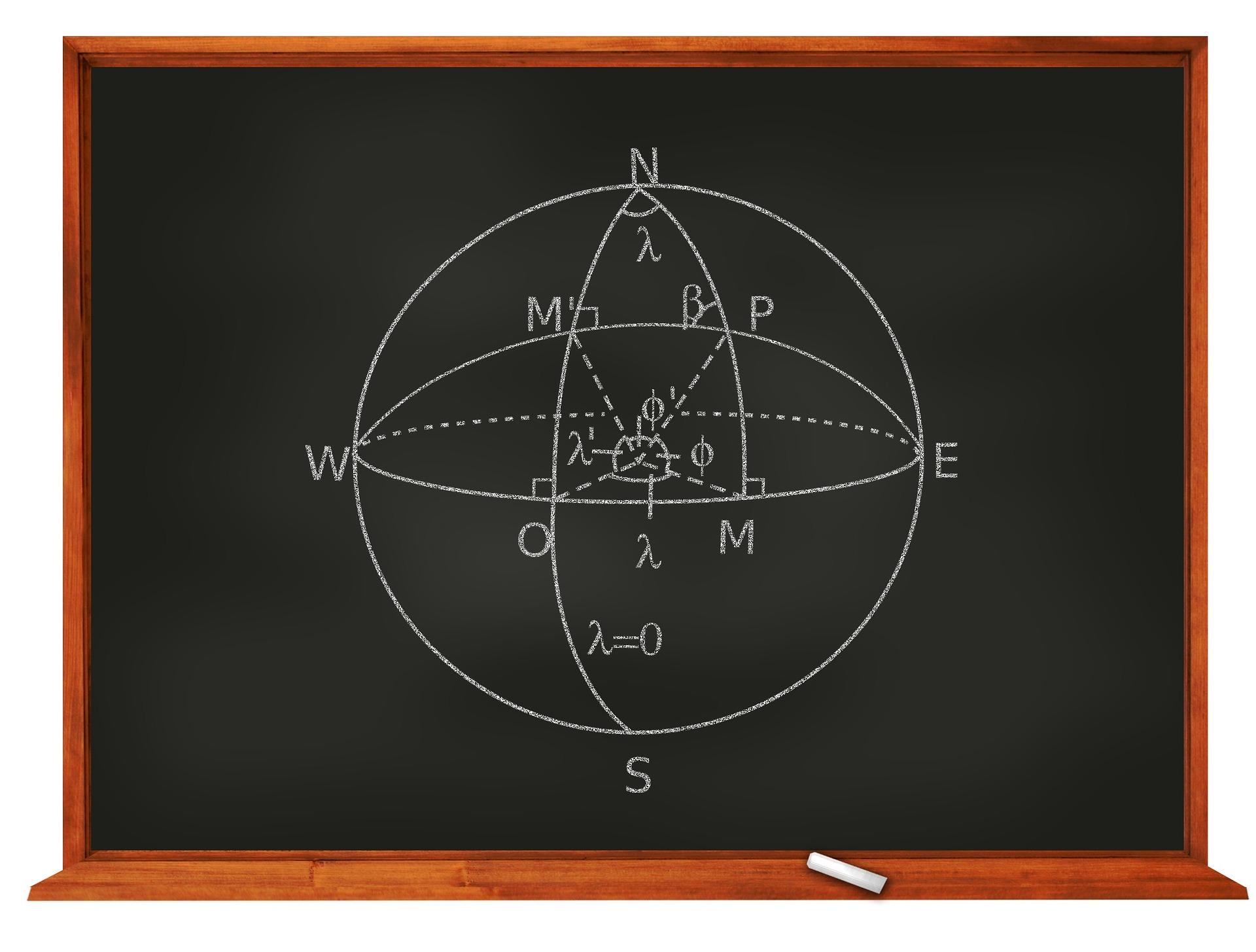
Les Suites
Comment étudie t-on une suite ? Introduction Une suite est une succession de termes, de nombres réels, qui nous permettent de traduire un problème, de comprendre une situation. Très utilisées en mathématiques, les suites sont ensuite appliquées, par exemple à l'économie, dans les banques ou les assurances. Le raisonnement par récurrence Définition La récurrence est[…]
15 mai 2019 ∙ 6 minutes de lecture

Limites et Continuité
Qu'est ce que la continuité ? Introduction On parle souvent, en mathématique, de fonctions continues. Mais qu'est ce que c'est ? De manière très simplifiée, on dit qu'une fonction continue est une fonction que l'on peut tracer sans lever le crayon. Ici, nous allons définir cette notion plus précisément. Définition de la continuité Pour comprendre[…]
2 mai 2019 ∙ 5 minutes de lecture

La Probabilité Conditionnelle
Comment déterminer si un jeu va vous faire gagner ? Vocabulaire - L'ensemble des issues d'une expérience aléatoire est appelé univers. En général, il est noté Ω et les issues sont notées, e1, e2, e3, en lorsqu'il y a n issues. Ainsi Ω = { e1, e2, e3, en }. - Un événement est une[…]
10 avril 2019 ∙ 7 minutes de lecture

Exercices : les Lois de la Probabilité
Que faut-il savoir et que faut-il faire avant de commencer un exercice sur les probabilités ? Probabilité et indépendance Si on considère A et B comme deux événements, sachant que A est un événement de probabilité non nulle, alors on peut définir la probabilité de B sachant A par la formule suivante : On appelle[…]
20 février 2019 ∙ 7 minutes de lecture

Variation d’une Suite
Révision de mathématiques Voici une petite fiche pour récapituler les différentes méthodes pour étudier le sens de variation d'une suite. 1) Etudier le signe de (Un+1) - (Un). - Si (Un+1) - (Un) ≥ 0 alors la suite (Un) est croissante. - Si (Un+1) - (Un) ≤ 0 alors la suite (Un) est décroissante. -[…]
21 septembre 2014 ∙ 1 minute de lecture

Les Inéquations Bicarrées
Comment les résoudre ? Présentation pour resoudre :2x4-9x2+4<0 on pose: 2x4-9x2+4=0 puis X=x2 on obtient : 2x2-9x+4=0 cherchons Δ=b2-4ac=(-9)2-4(2)(4)=81-32=49 Δ>0 d'ou: X1=(-b-√Δ)/2a X2=(-b+√Δ)/2a X1=(9-7)/2(2) =1/2 X2=(9+7)/2(2)=4 revenons a :x2=X x2=1/2 x2=4 x2=-√2/2 ou x2=√2/2 x2=-2 ou x2=2 apres factorisation on obtient: 2x2-9x+4=a(x2-X1)(x2-X2)=2(x2-1/2)(x2-4) mettons les resultats dans un tableau: Tableau x -∞ -2 -√2/2 √2/2 2 +∞ x2-1/2 + +[…]
3 avril 2011 ∙ 1 minute de lecture

Mémento de Mathématiques en Terminale Scientifique
Que faut-il connaître pour bien réussir l'épreuve ? Fonctions exponentielles e0 = 1. Pour tous réels a et b : ea+b = ea eb ; ea-b = ea / eb ; (ea)b = eab Pour tous a et b de ] 0 ; +∞ [ : ln(ab) = ln(a) + ln(b) ; ln(a/b) = ln(a)[…]
2 mars 2011 ∙ 2 minutes de lecture

Résumé des Notions Importantes en Terminale
Que faut-il savoir pour réussir le BAC ? Forme algébrique FORME ALGÉBRIQUE : z = x + iy i2 = -1 Partie réelle : Re(z) = x Partie imaginaire : Im(z) = y Module l z l = OM = √( zz/ ) = √( x2 + y2 ) Forme trigonométrique FORME TRIGONOMÉTRIQUE ( z[…]
2 mars 2011 ∙ 3 minutes de lecture
Cours sur les Nombres Complexes
Comment résoudre les équations ? Introduction L'equation x²=a, lorsque a<0 , n'a pas de solution réelle. On adopte un nombre dont le carré vaut (-1). (Ce n'est pas une réel). Ce nombre n'est pas noté √(-1) car il ne coinciderait pas avec les formules sur les racine carré. √(ab) = √(a) √(b) , D'une part[…]
7 décembre 2010 ∙ 2 minutes de lecture
Introduction à la Fonction Exponentielle
Comment trouver une image ? Introduction On admet qu’il existe une unique fonction définie dérivable sur R, tel que : -Pour tout x appartenant à R, f’(x)=f(x) -f(o)=1 Théorème 1)Pour tout x appartenant à R, f(x)*f(-x)=1 2) Pour tout x appartenant à R, f(x) différent de 0 3) Pour tout x appartenant à R, f(x)>0. Démonstration[…]
4 décembre 2010 ∙ 2 minutes de lecture

Exercice Corrigé sur les Équations Différentielles
Comment comprendre ce type de questions ? Exercice 1 1) (E)) : y'+y = x+1 a) z = y-x z+x = y z'+1 = y' donc (E) devient : z'+1+z+x = x+1 (F) : z'+z = 0 b) (F) : z' = -z forme y' = ay avec a = -1 les fonctions solution sont : x→ke-x , k є[…]
3 décembre 2010 ∙ 1 minute de lecture

L’Équation Différentielle
Comment résoudre ce type d'exercice BAC ? Exercice 1 On se propose de résoudre l'équation différentielle (E) : y' + y = x + 1 , y étant une fonction de la variable réelle x et y' sa dérivée. a) On pose z=y-x ; écrivez l'équation différentielle (F) satisfait par z. b) Résolvez (F), puis[…]
3 décembre 2010 ∙ 1 minute de lecture

Exercice Corrigé sur l’Exponentielle et les PPI
Quelles étaient les bonnes réponses ? Exercice f(x) = (3-x)ex Démontrons que l'équation f'(x) = 2 a exactement 2 solutions. f'(x) = -ex+(3-x)ex f'(x) = ex(2-x) Soit l'equation : ex(2-x) = 2 <=> ex(2-x)-2 = 0 On pose g la fonction définie sur IR par g(x) = ex(2-x)-2 g'(x) = ex(2-x)+ex(-1) = ex(1-x) ∀x Є IR,[…]
24 novembre 2010 ∙ 1 minute de lecture
