Chapitres
En mathématiques, une levée de fonction d'une forme indéterminée fait référence à une méthode utilisée pour déterminer la limite d'une fonction lorsque son expression est de type indéterminé, c'est-à-dire lorsqu'il est impossible de l'évaluer directement.
? Cette méthode consiste à transformer l'expression indéterminée en une forme équivalente qui permet de simplifier le calcul de la limite
On utilise souvent des règles algébriques telles que :
La factorisation
La manipulation des fractions
L'utilisation des limites connues
? La levée de fonction d'une forme indéterminée est une approche utile pour résoudre des problèmes mathématiques où la limite d'une fonction est nécessaire pour obtenir un résultat précis.
Définition d'une limite
La limite d'une fonction en un point "a" est la valeur vers laquelle va tendre la fonction au point a, parfois sans jamais ne l'atteindre.
- Soit f une fonction continue
- Lorsque une fonction f est définie au point a, sa limite en a est f(a)
- On note
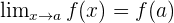
- Lorsque une fonction f n'est pas définie au point a, on étudie la limite au point a.
C'est le cas notamment en +∞ et -∞. On cherche à comprendre vers quelle valeur tend la fonction en sachant qu'elle ne l'atteint jamais.
❌ Il est important de connaître les limites de quelques fonctions de base :
- La fonction carré tend vers l'infini en +∞ et -∞
- La fonction inverse tend vers 0 lorsque x tend vers +∞ ou -∞
- En 0-, la fonction tend vers -∞ et en 0+ la fonction tend vers +∞
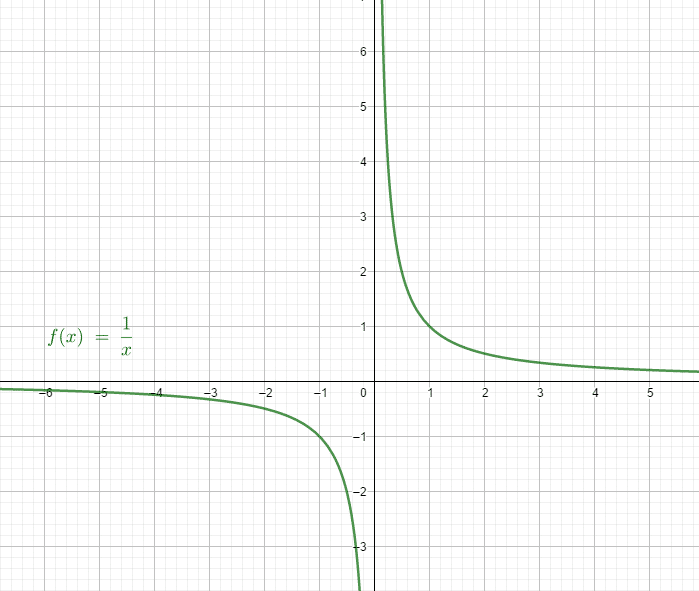
✅ La fonction exponentielle est toujours positive
Elle tend vers l'infini lorsque x tend vers l'infini et tend vers 0 lorsque x tend vers -∞.
La fonction logarithme est défini uniquement sur l'intervalle ]0,+∞[. Elle tend vers -∞ lorsque x tend vers 0 et vers l'infini lorsque x tend vers l'infini.
Propriétés et formes indéterminées
Les formes indéterminées sont :
Pour calculer les limites de fonctions, quelques propriétés sont à connaître concernant :
La somme
Le produit
Le quotient
On répertorie ses propriétés dans des tableaux en précisant les formes indéterminées, à savoir :
- Limites de somme
| lim Un | L | L | L | +∞ | +∞ |
|---|---|---|---|---|---|
| lim Vn | L' | +∞ | -∞ | +∞ | -∞ |
| lim (Un+Vn) | L+L' | +∞ | -∞ | +∞ | forme indéterminée |
- Limites de produit
| lim Un | L | L>0 | L>0 | L<0 | L<0 | +∞ | +∞ | -∞ | 0 |
|---|---|---|---|---|---|---|---|---|---|
| lim Vn | L' | +∞ | -∞ | +∞ | -∞ | +∞ | -∞ | -∞ | +∞ ou -∞ |
| lim (Un x Vn) | L x L' | +∞ | -∞ | -∞ | +∞ | +∞ | -∞ | +∞ | forme indéterminée |
- Limites de quotient
| lim Un | L | L | +∞ | -∞ | L≠0 | 0 | +∞ ou -∞ |
|---|---|---|---|---|---|---|---|
| lim Vn | L'≠0 | +∞ ou -∞ | L≠0 | L≠0 | 0 | 0 | +∞ ou -∞ |
| lim (Un/Vn) | L/L' | 0 | +∞ si L>0 -∞ si L<0 | -∞ si L>0 +∞ si L<0 | +∞ ou -∞ | forme indéterminée | forme indéterminée |
De plus, certaines limites concernant les exponentielles et les logarithmes sont à connaître.
La fonction exponentielle croit plus vite que x, ainsi on a :
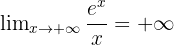
Pour tout n entier naturel,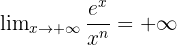 
- De même,
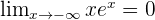
- Pour tout n entier naturel,
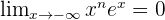
A l'inverse, la fonction logarithme croit moins vite que x.
- On a alors
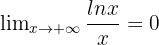
Pour tout entier naturel n,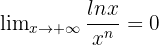 
- De même,
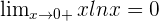
Pour tout entier naturel n,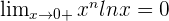 
On appelle cela la croissance comparée. Ces limites nous permettent d'éviter des formes indéterminées.
Techniques pour résoudre les formes indéterminées
Il existe trois méthodes principales pour réaliser le calcul des formes indéterminées :
- Mettre en facteur le terme dominant, le terme de plus haut degré
- Utiliser les croissances comparées
- Utiliser le taux d'accroissement, la fonction dérivée
Mettre en facteur le terme dominant, le terme de plus haut degré
Premier exemple
Par exemple, calculons la limite en +∞ de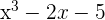 
.
? On observe une forme indéterminée ∞-∞.
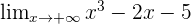
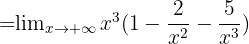
- Comme [-\frac{2}{x^2}[/latex] et [-\frac{5}{x^3}[/latex] tendent vers 0 en l'infini,
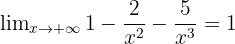et 
. ✍? On note la forme indéterminée
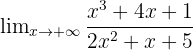
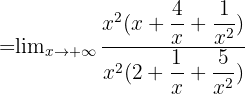
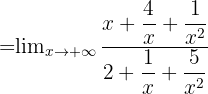
- La limite du numérateur est +∞ et la limite du dénominateur est 2
- Par quotient, la limite de la fonction en l'infini est +∞
? On en déduit une propriété : la limite d'une fonction rationnelle en +∞ et en -∞ est égale à la limite du rapport du terme de plus haut degré du numérateur par le terme de plus haut degré du dénominateur.
Enfin, regardons un exemple composé de racine carrée. Cherchons la limite en -∞ de
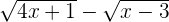
- On a la forme indéterminée ∞-∞.
- On factorise sous les racines par x.
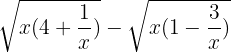
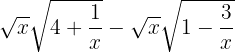
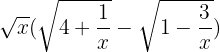
- On a
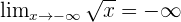et 
- On sait, par croissance comparée, que
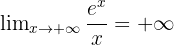
- D'où, par somme,
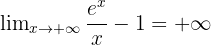
- Enfin, par produit de limites, comme
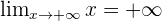alors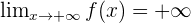 
Utiliser le taux d'accroissement, la fonction dérivée
On utilise principalement cette solution lorsque l'on se retrouve face à la forme indéterminée
Par exemple, on cherche la limite en 0 de
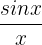
- On a la forme indéterminée
- On pose f(x)= sin x
- On sait que la dérivée de sin x est cos x
- On a alors
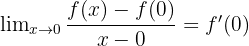
- Ainsi,
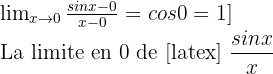est 1.
? Pour éliminer la forme indéterminée
, on peut également utiliser la règle de l’hôpitalCelle-ci dit que, si f et g sont deux fonctions dérivables en a telles que f(a)=g(a)=0 et g'(a) non nul alors
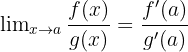
Prenons pour exemple la fonction rationnelle
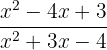et cherchons sa limite en 1. - On remarque la forme indéterminée
- On applique la règle de l’hôpital
- La dérivée du numérateur est 2x-4 et la dérivée du dénominateur est 2x+3
- Appliqué au point 1, on obtient -2 et 5
- Ainsi,
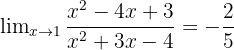
- La limite de notre fonction rationnelle au point 1 est
Vous voilà désormais équipé pour faire face à votre prochain problème de mathématiques.
Vous avez aimé cet article ? Notez-le !
Loading...
Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Bonjour je veux trouver la limite de ce quotient: lim[ln(x)]/x quand x tends vers 0,
En effet, on sait que lim[lnx]=-infini quand x tends vers 0, on a la forme indéterminée -infini/0??.
Merci
Bonjour Akab,
Merci pour votre message.
Pour résoudre correctement ce type de limite et comprendre les formes indéterminées, nous vous recommandons de contacter un professeur particulier de mathématiques sur Superprof.
Un enseignant pourra vous accompagner pas à pas et vous aider à maîtriser ces notions.
N’hésitez pas à consulter les profils disponibles sur la plateforme !
c’est cool pour moi
Merci de nous apporter votre aide . merci
Bonsoir. J’ai trouvé super bien la technique pour lever l’indétermination. Merci
Comment expliquer moi
corriger l’exercice qui contient les racines carrés.
x tend vers plus l’infini et non pas tend vers moins
l’infini. merci.
Merci pour vos efforts et demeurez dans cette excellence
sqrt(x) n’étant pas défini en moins l’infini, sa limite en moins l’infini ne peut pas tendre vers moins l’infini.