Résolution Graphique en Seconde
Comment peut-on étudier la courbe représentative d'une fonction ? Sujet On donne f : x → x2 + 3x + 2 Résoudre graphiquement : f(x) ≥ 2 f(x) < 0 f(x) = 3x + 3 Solution Dans le cadre de la création de la représentation graphique de la fonction f, on crée un tableau de[…]
11 juin 2008 ∙ 1 minute de lecture
Algèbre en Seconde
Comment faut-il procéder pour résoudre une équation complexe ? Sujet On considère l'expression C = 4x2 - 25 - 2( 2x - 5 )2 Développer et réduire C. Factoriser C. Résoudre les équations : C = 0 C = -75 C = 2x - 15 Solutions 1. C = 4x2 - 25 - 2( 2x[…]
11 juin 2008 ∙ 2 minutes de lecture
Effectifs et Fréquences Cumulés
A quoi correspondent les effectifs et fréquences cumulé(e)s croissant(e)s et / ou décroissant(e)s ? Effectifs et fréquences cumulé(e)s croissant(e)s et / ou décroissant(e)s Dans le cas d'une variable quantitative, on peut ordonner les différentes valeurs de la variable dasn l'ordre croissant ou décroissant. On peut déterminer " Quel effectif ou quelle fréquence de la population[…]
26 avril 2008 ∙ 1 minute de lecture
Effectifs et Fréquences
Que faut-il absolument savoir lorsqu'on débute ce thème ? Effectifs et fréquences On appelle effectif d'une valeur le nombre d'individus de la population possédant le caractère de cette valeur. On appelle fréquence d'une valeur le quotient de l'effectif de cette valeur par l'effectif total de la population. Les fréquences sont des nombres compris entre 0[…]
26 avril 2008 ∙ 1 minute de lecture
Liste de Vocabulaire sur les Statistiques
Que faut-il savoir concernant ce thème mathématique ? Ce qu'il faut savoir Une étude statistique s'effectue sur un ensemble appelé population, dont les éléments sont appelés les individus, et consiste à observer et étudier un même aspect sur chaque individu, appelé caractère. On distingue deux types de caractère : Les caractères qualitatifs : ce sont les caractères[…]
12 avril 2008 ∙ 1 minute de lecture
Méthodes en Algèbre
Comment travailler ses mathématiques pour le baccalauréat ? Pour factoriser On repère un facteur commun et on le met en facteur commun. Ex. : x²-4x = x(x-4) On cherche une identité remarquable. S'il n'y vraiment pas de facteurs communs ou d'indentité remarquable, on développe puis on factorise ensuite. Ex. : (x-1)(x+4)-(x-2)(x+3)= x²+4x-x-4-x²-3x+2x+6 = 2x+2 = 2(x+1) Pour[…]
14 mars 2008 ∙ 2 minutes de lecture
Les Ensembles de Nombres
Comment sont classés les nombres existant ? L'ensemble des entiers naturels Les entiers naturels sont les nombres entiers positifs ou nul. désigne l'ensemble des entiers naturels. ={0;1;2;3;4;5;6...} L'ensemble des entiers relatifs Les entiers relatifs sont les nombres entiers positifs, négatifs ou nul. désigne l'ensemble des entiers relatifs. ={...-4;-3;-2;-1;0;1;2;3;4...} L'ensemble des décimaux Un décimal est un[…]
1 mars 2008 ∙ 1 minute de lecture
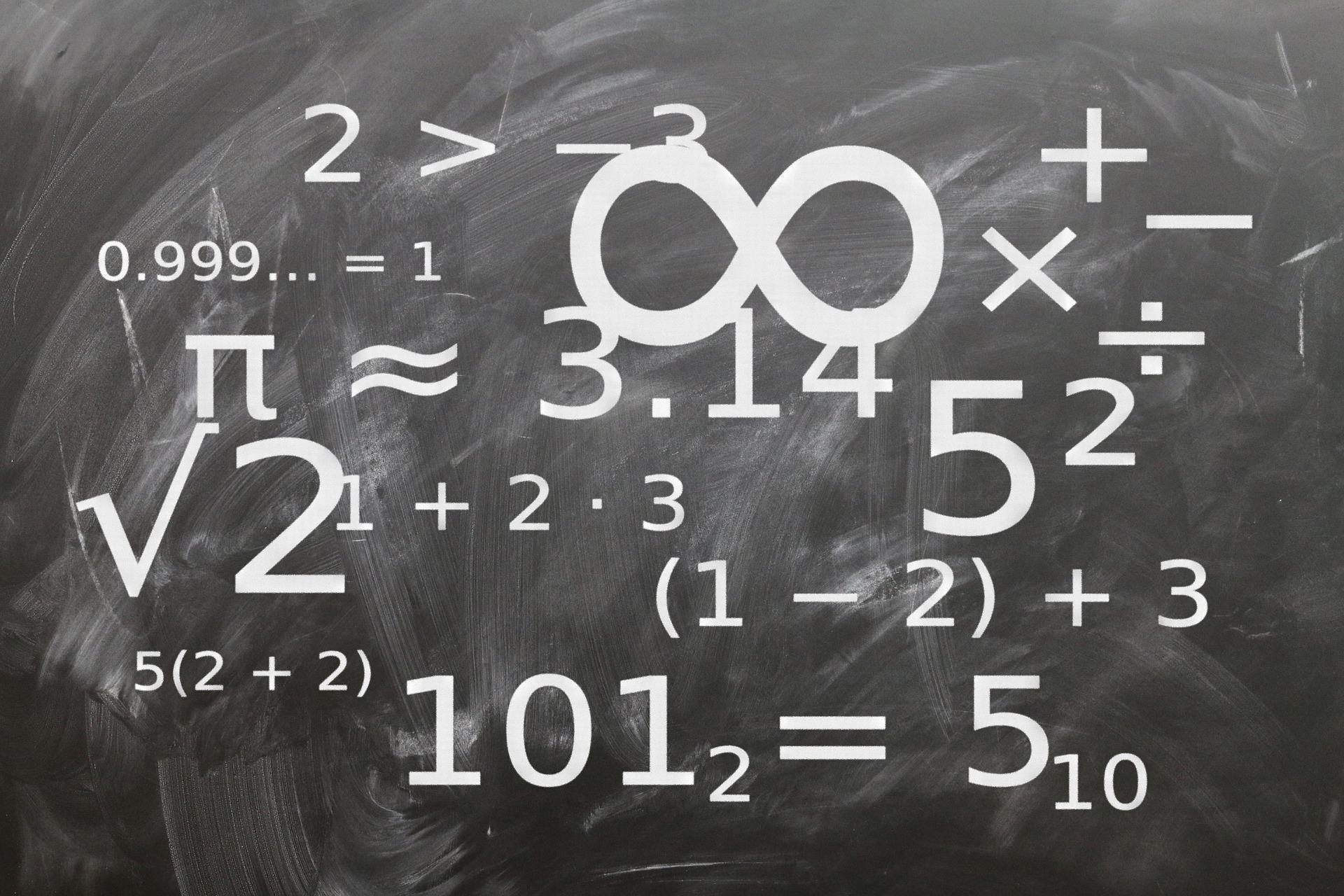
Les Intervalles
Comment comprendre l'ordre, la valeur absolue et les inéquations ? Définition On appelle un intervalle l'ensemble des nombres déterminés par une inégalité ou un encadrement. Intervalles bornés L'ensemble des réels x tels que a x b est noté [a ; b]. L'ensemble des réels x tels que a x b est noté ]a ; b[.[…]
20 février 2008 ∙ 2 minutes de lecture
Les Opérations sur les Inégalités
Comment comprendre les thèmes du programme ? Addition ♦ Si a < b alors a + c < b + c. ♦ Si a < b alors a - c < b - c. ♦ Si a < b et c < d alors a + c < b + d. Exemples : Si x[…]
19 février 2008 ∙ 2 minutes de lecture
Vocabulaire des Fonctions
Comment comprendre son énoncé de mathématique ? Courbe représentative Le plan est muni d'un repère orthogonal (O,I,J). Soit f une fonction définie sur un intervalle D. On appelle courbe représentative (C) de la fonction f sur D, l'ensemble des points M (x,y) tels que : x € (appartient) D et y = f(x) Parité d'une[…]
3 février 2008 ∙ 1 minute de lecture
Propriétés et Définitions en Mathématiques
La géométrie dans l'espace 1) Généralités -Deux points distincts A et B déterminent une unique droite (AB). -Trois points (distincts) non alignés déterminent un unique plan ou une droite et un point qui n'appartient pas à cette droite déterminent un unique plan. 2) Positions relatives de 2 droites Définition: 2 droites de l'espace sont coplanaires si elles sont dans un même plan. A°Droites coplanaires: 3 posibilités.[…]
6 décembre 2007 ∙ 2 minutes de lecture
Les Inégalités Remarquables
Les expressions inégales en mathématiques 1.Valeur absolue DÉFINITION 1. Soit a , on définit la valeur absolue de a (noté |a|), le plus grand nombre entre a et -a: 1. Pour tout a , il résulte |a| > 0 et |a| = 0 si, et seulement si, a = 0. a < |a| et -a[…]
2 novembre 2007 ∙ 1 minute de lecture
Notions d’Ensemble en Mathématiques
Les grands ensembles numériques => On appelle N, l'ensemble des entiers naturels : {0,1,2,3,...} =>On appelle Z, l'ensemble des entiers relatifs : {...,-3,-2,-1,0,1,2,3,...} =>On appelle D, l'ensemble des nombres décimaux. Ce sont tous els nombres qui peuvent s'écrire sous la forme d'une fraction : a/10 où a est un entier relatif et la puissance potentiel[…]
31 octobre 2007 ∙ 1 minute de lecture
Les Configurations Planes en Géométrie
Les transformations de la configuration axiale 1) Symétrie axiale ou orthogonale La symétrie orthogonale par rapport à la droite (d) se note S(d). Le point N est un point invariant. M' est l'image de M par la symétrie S(d) si : la droite (d) est la médiatrice du segment [MM']. 2) Symétrie centrale La symétrie[…]
26 octobre 2007 ∙ 1 minute de lecture
Les Comparaisons de Nombres
Comparer deux réels avec des signes 1) Rappel Définition : Comparer deux réels, c'est dire s'ils sont égaux ou sinon dire lequel est le plus grand ou le plus petit. Soit a ∈ et b ∈ : a ≤ b signifie que b – a ∈ + c'est-à-dire b – a ≥ 0. Pour comparer deux réels,[…]
16 octobre 2007 ∙ 2 minutes de lecture
Exercices sur les Vecteurs en Mathématiques
Travail sur la vectorisation géométrique Exercice 1 Soit ABC un triangle non aplati. Soit A’, B’, C’ les milieux respectifs des segments [BC], [AC] et [AB]. Soit G le point d’intersection des droites (BB’) et (CC’). Soit B1 le symétrique de G par rapport à B’ et C1 le symétrique de G par rapport a[…]
14 octobre 2007 ∙ 2 minutes de lecture
Les Nombres et leurs Ensembles
Les différents ordres de chiffres et entiers I ) Nombres entiers et nombres premiers Définiton : On appelle nombre premier tout entier nbaturel qui possède exactement deux diviseurs : 1 et lui-même. Remarque : tout entier naturel (différent de 1) qui n'est pas premier, est dit composé. Théorème : Tout nombre entier supérieur à 2[…]
14 octobre 2007 ∙ 3 minutes de lecture
Devoir Maison de Seconde
Répondre aux questions de géométrie et d'algèbre exo1 soit ABCD un carré de centre O,I milieu de [AD] et J celui de [AB].L'objet de ce probléme est de montrer que les droites (CJ)et (BI) sont perpendicculaires. soit K le point d'intersection de (BC) et de la paralléle à (BI) passant par A 1.FAIRE LA FIGURE[…]
10 octobre 2007 ∙ 1 minute de lecture
Le Crible d’Ératosthène
Déterminer les nombres premiers inférieurs à 100 Voici la grille contenant les nombres de 1 à 100. On élimine 1 et tous les multiples de 2, sauf 2. On élimine les multiples de 3 restant, sauf 3. On élimine les multiples de 5 restant, sauf 5. On élimine les 3 multiples de 7 restant, sauf[…]
30 septembre 2007 ∙ 1 minute de lecture
Les Intervalles des Nombres Réels
Les ensembles compris entre deux valeurs 1) Définition Soient a et b deux réels tels que a < b. ]a ; b[ = {x ∈ ; a < x < b} [a ; b] = {x ∈ ; a ≤ x ≤ b} [a ; b[ = {x ∈ ; a ≤ x < b} ]a ; b][…]
30 septembre 2007 ∙ 2 minutes de lecture
Développement et Factorisation
Développer ou factoriser une expression 1) Identités remarquables développement factorisation développement factorisation développement factorisation Exemples : 2) Développement Développer un produit, c'est le transformer en somme ou en différence. k(a + b) = ka + kb k(a – b) = ka – kb (a +[…]
20 septembre 2007 ∙ 1 minute de lecture
Les Nombres Premiers en Mathématiques
Les chiffres divisibles par 1 ou eux-mêmes Dans ce paragraphe, on se place dans l'ensemble 1) Diviseurs Définition : Soient a et b deux entiers naturels avec b ≠ 0. a ∈ et b ∈ * On dit que b est un diviseur de a s'il existe un entier naturel n tel que a = n[…]
20 septembre 2007 ∙ 2 minutes de lecture
Les Ensembles de Nombres
Les groupes numériques faisant partie du réel 1) Nombres entiers Définition : L'ensemble des nombres entiers naturels se note = {0 ; 1 ; 2 ; 3 ; ...} Définition : L'ensemble des entiers relatifs se note = {... ; -3 ; -2 ; -1 ; 0 ; 1 ; 2 ; 3 ; ...}[…]
20 septembre 2007 ∙ 2 minutes de lecture
Résumé : les Nombres Premiers
Des identités remarquables des mathématiques Un nombre entier naturel n est dit premier si, et seulement si, il est divible par 1 et lui même. 0 et 1 ne sont pas des nombres premiers. Tout nombre entier naturel n, autre que 1, admet au moins un diviseur premier. Tout nombre entier naturel n, non premier,[…]
16 septembre 2007 ∙ 1 minute de lecture
Entraînement de Mathématiques en Troisième
Correction d'exercices de maths Exercice 1 Expression en lettres Expression en chiffres La somme de a et de b : a + b Le double de a : 2a Le carrée de b : b² L'inverse de c : 1 c Le carré du double de a : (2a)² Le double du carré de a : 2a² Le double du produit[…]
9 septembre 2007 ∙ 2 minutes de lecture
Résumé : les Ensembles de Nombres
Cours sur les groupes de chiffres 1°) L'ensemble des entiers naturels N N= {0;1;2;3;4;5;...} 2°) L'ensemble des entiers relatifs Z Z= {...;-3;-1;0;4;12;...} Remarque:N C Z 3°) L'ensemble des nombres décimaux D D= {1;1,-5,2;0;-12;5/2=2,5;...} définition:un nombre décimal contient une partie entière et une partie décimal finie. 4°) L'ensemble des nombres rationnels Q définition:un nombre rationnel est[…]
9 septembre 2007 ∙ 1 minute de lecture
Exercice de Géométrie sur un Triangle
Entraînement et correction géométrique Question Soit ABC un triangle quelconque, on construit un rectangle ABFE à l'extérieur de ce triangle de base [AB] et de hauteur quelconque [AE]. On construit le point G transformé de C par la translation qui transforme E en A. On trace la parallèle à (AC) et à (BC) passant par[…]
8 septembre 2007 ∙ 1 minute de lecture
Exercices de Révision de Troisième
Entraînement aux bases pour le lycée Exercice 1 Compléte la partie manquante. Expression en lettres Expression en chiffres La somme de a et de b : ………… Le double de a : ………… Le carrée de b : ………… L'inverse de c : ………… Le carré du double de a : ………… Le double du carré de a : ………… Le[…]
7 septembre 2007 ∙ 1 minute de lecture
Les Intervalles de R en Mathématiques
Les sous-ensembles des réels en maths Les intervalles réels sont des sous-ensembles (ou des parties) de l'ensemble des réels . Leur grande particularité est qu'ils sont "continus". C'est-à-dire que le chemin entre deux éléments d'un intervalle reste dans cet intervalle. Leur représentation sur la droite numérique est un segment ou une droite dont les extrémités[…]
22 août 2007 ∙ 2 minutes de lecture