Le Second Degré et les Equations
Quelle méthode faut-il utiliser pour les résoudre ? Définition Une équation du second degré a pour forme générale ax²+bx+c=0. Pour résoudre ce type d'équations, on factorise soit en trouvant un facteur commun, soit grâce aux identités remarquables. Une équation du second degré peut avoir 0, 1 ou 2 solutions. Méthode pour résoudre une équation du[…]
1 juin 2009 ∙ 2 minutes de lecture
Equation de Droite
Comment déterminer y=f(x) ? Le plan est rapporté à un repère (O,I,J) Caractérisation d'une équation de droite Soit l'équation à deux inconnues y = 3x - 2. Recherchez 5 couples solutions de cette équation. Représentez dans un repère les points associés. Recherchons des solutions. Il faut choisir une valeur pour x puis calculons la valeur[…]
1 juin 2009 ∙ 10 minutes de lecture
Exercice sur les Nombres Premiers
Es-tu prêt pour le prochain devoir surveillé ? Exercice Démontrer que : Si p est un nombre premier supérieur ou égal à 3, alors p + 1 n'est pas premier. Réponse un nombre premier supérieur à 3 est forcément impair (sinon il serait divisible par 2 et donc il ne serait plus premier) donc si[…]
27 mai 2009 ∙ 1 minute de lecture
Les Statistiques au College
Que permet la mise au point de statistiques ? Introduction Les études statistiques permettent de recueillir des données. On distingue deux sortes de données, selon leur nature. Si l'on s'intéresse à un phénomène de nature numérique (l'âge des personnes interrogées, leurs tailles…), on dit alors que les données sont quantitatives. Elles peuvent être rangées dans[…]
27 mai 2009 ∙ 2 minutes de lecture
Le Carré d’un Nombre
A quoi correspond la fonction carrée ? Rappels Propriétés du carré d'un nombre réel : Le carré d'un nombre réel est positif ou nul, c'est-à-dire : quel que soit le nombre réel x, x²≥0. Deux nombres réels opposés ont même carré, c'est-à-dire : quel que soit le nombre réel x, (-x)² = x². Produits remarquables[…]
26 mai 2009 ∙ 1 minute de lecture
La Valeur Absolue
Comment la trouver ? Définition La valeur absolue d'un nombre réel x est définie par : | x | = x si x > 0 | x | = -x si x < 0 On en déduit donc que | x | ≥0 quelque soit x. Inégalité triangulaire a,b,c trois nombres : | a +[…]
25 mai 2009 ∙ 1 minute de lecture
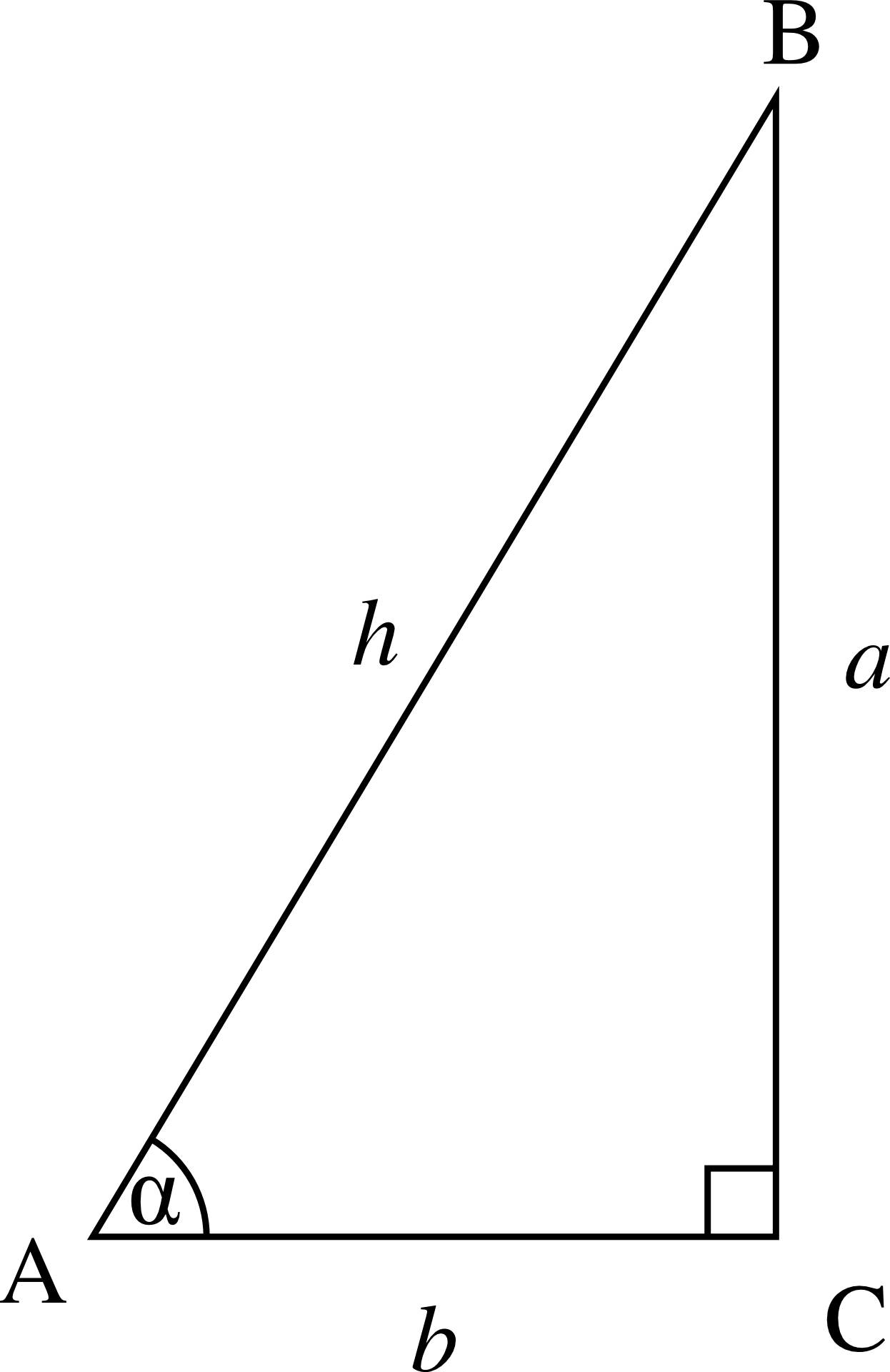
Droites Remarquables d’un Triangle
Comment les tracer ? Médiatrices d'un triangle Définition : Dans un triangle, la médiatrice d'un côté est la droite qui coupe ce côté perpendiculairement et en son milieu Propriété 1 : La médiatrice d'un segment est l'ensemble des points situés à égale distance des extrémités de ce segment. Propriété 2 : Les trois médiatrices d'un[…]
25 mai 2009 ∙ 1 minute de lecture
Angles au Centre et Angles Inscrits
Comment les calculer ? Angles au centre Dans un cercle, un angle au centre est un angle dont le sommet est le centre du cercle. => L'angle saillant est l'angle au centre interceptant l'arc . Angles inscrits dans un cercle Dans un cercle, un angle inscrit est un angle dont le sommet est un point[…]
24 mai 2009 ∙ 1 minute de lecture
Simplifier des Racines Carrées
Comment faut-il procéder ? Ici: « V » représente le symbole de la racine. Et «# » signifie « différent de » Simplifier des calculs contenant des racines carrées Simplifier une racine carrée signifie rendre le nombre entier situé sous la racine le plus petit possible. Pour cela, on applique la méthode suivante : Ex[…]
23 mai 2009 ∙ 2 minutes de lecture
Exercices sur les Identités Remarquables
Comment bien se préparer sur ce sujet ? Développer les expressions suivantes 1) (2x-5)² expression de la forme « (a-b)² » on doit donc obtenir un développement de la forme, « a²-2ab+b² » =(2x)²-2*2x*5+5² =4x²-20x+25 2) (2x+1)² expression de la forme « (a+b)² » on doit donc obtenir un développement de la forme, « a²+2ab+b²[…]
23 mai 2009 ∙ 1 minute de lecture
Exercices Types sur les Racines Carrées
Comment les calculer ? "V" signifie "racine de" Développer et réduire A=(3-V2)(3+V2) Nous avons une identité remarquable de la forme "(a-b)(a+b)" qui est égale à "a²-b²" =3²-(V2)² =9-2 =7 B=(5+V7)(5-V7) Nous avons une identité remarquable de la forme "(a+b)(a-b)" qui est égale à "a²-b²" =5²-(V7)² =25-7 =18 C=(V6-3)(3+V6) =(V6-3)(V6+3) Nous avons une identité remarquable de[…]
23 mai 2009 ∙ 1 minute de lecture
Exercices sur les Racines Carrées
Comment résoudre ce genre de problème ? "V" signifie "racine de" Calculer A=V49 =V(7²) =7 B=-5V16 =-5V(4²) =-5*4 =-20 C=2V9 =2V(3²) =2*3 =6 D=V16/V36 =V(4²)/V(6²) =4/6 =2/3 Simplifier et donner le résultat sous la forme aVb A=3V18-V2+5V8 =3V(2*3²)-V2+5V(2*2²) =3V2*V(3²)-V2+5V2*V(2²) =3*3V2-V2+2*5V2 =9V2-V2+10V2 =(9-1+10)V2 =18V2 B=6V3+2V75 =6V3+2V(3*5²) =6V3+2V3V(5²) =6V3+2*5V3 =6V3+10V3 =(6+10)V3 =16V3 C=V160+3V40 =V(2*5*4²)+3V(2*5*2²) =V2*V5*V(4²)+3V2*V5*V(2²) =4V2*V5+3*2V2*V5 car[…]
23 mai 2009 ∙ 1 minute de lecture
Interprétation Graphique d’un Système
Qu'est-ce que la forme réduite ? Interprétation graphique d'une équation à deux inconnues Toute équation de la forme : ax+by+c=0 est une équation cartésienne d'une droite. Exemple : 2x+3y=5 Cette équation peut être mise sous forme réduite, et on obtient alors y=-(2/3)x+(5/3) On retrouve donc bien la forme usuelle de l'équation de droite (fonctions affines)[…]
22 mai 2009 ∙ 1 minute de lecture
Systèmes d’Équations à Deux Inconnues
Quelle méthode faut-il appliquer ? Principe Si l'on cherche à résoudre deux équations simultanément, on parle de systèmes d'équations. Les systèmes au programme de troisième comportent deux équations à deux inconnues, notées « x » et « y ». Un système de deux équations à deux inconnues est donc de la forme : {ax+by+c=0 {a'x+b'y+c'=0[…]
22 mai 2009 ∙ 1 minute de lecture
Les Fonctions Affines et leur Représentation Graphique
Comment la tracer ? Définition Une fonction affine est une fonction qui, à tout nombre « x », associe le nombre « ax+b ». On dit alors que « ax+b » est l'image de « x » par la fonction affine f. Exemple : Soit la fonction f définie par f(x)=3x-5 Calculer les images de[…]
22 mai 2009 ∙ 1 minute de lecture
La Résolution d’une Équation du Second Degré
Quelle est la bonne méthode ? Exercice Résoudre x²-16=(2x+1)(x+4) Correction Etape 1 :On place tous les termes de l'équation à gauche du signe égal, de façon à obtenir 0 à droite. On a alors: ²-16-(2x+1)(x+4)=0 Etape 2 :On factorise le côté gauche de léquation en utilisant la méthode de factorisation habituelle et/ou grâce aux identités[…]
22 mai 2009 ∙ 1 minute de lecture
La Factorisation
Comment factoriser ? Exercice 1) 3(4x-3)-(2-x)(4x-3) =(4x-3)[3-(2-x)] =(4x-3)(3-2+x) =(4x-3)(x+1) 2) (x+2)(x-5)-3x(x+2)+2(x-6)(x+2) =(x+2)[(x-5)-3x+2(x-6)] =(x+2)[x-5-3x+2x-12] =(x+2)(0x-17) =(x+2)(-17) =-17(x+2) 3) (8x-5)+2(5-8x)-(3x+2)(16x-10) = (8x-5)-2(-5+8x)-(3x+2)*2(8x-5) = 1(8x-5)-2(8x-5)-2(3x+2)(8x-5) =(8x-5)[1-2-2(3x+2)] =(8x-5)[-1-6x-4] =(8x-5)(-6x-5) 4) 2x+5-3(5-2x)+4(3x-8)(10-4x) =(-2x+5)-3(-2x+5)+4(3x-8)*2(-2x+5) = 1(-2x+5)-3(-2x+5)+8(3x-8)(-2x+5) =(-2x+5)[1-3+8(3x-8)] =(-2x+5)[-2+24x-64] =(-2x+5)(24x-66) = (-2x+5)*2(12x-33) =2(-2x+5)(12x-33) Correction
22 mai 2009 ∙ 1 minute de lecture
Les Équations du Deuxième Degré
Quelles sont leurs particularités ? Résoudre les équations produits a) (x-5)(x+3)=0 Un produit de facteurs est nul si l'un au moins de ses facteurs est nul. Soit x-5=0 donc x=5 Soit x+3=0 donc x=-3 Les solutions de l'équation sont : 3 et 5 b) (3x-1)(x-7)=0 Un produit de facteurs est nul si l'un au moins[…]
22 mai 2009 ∙ 2 minutes de lecture
Exemple d’Application sur les Fonctions Linéaires
Quelles sont ses particularités ? Exercice Soient les fonctions f(x)=-(1/2)x et g(x)=-2x+6 1)f et g sont-elles linéaires ? Affines ? En déduire la nature de leur représentation graphiques respectives. 2) Calculer les images de 2 ;-1 ;0 ;3 et 3/4 par « f » puis par « g » 3) Calculer les antécédents de 3[…]
21 mai 2009 ∙ 2 minutes de lecture
L’Équation du Premier Degré
Comment calculer des approximations ? Résoudre et donner la valeur exacte de la solution de chaque équation (pas de résultat en décimales) a) 5x+3 = 19x+1/2 5x-19x=1/2-3 -14x=1/2-6/2 -14x=-5/2 -x=-5/(2*14) -x=-5/28 x=5/28 b) 8x-4=4x+1 8x-4x=1+4 4x=5 x=5/4 c) 3(2x+1)=8x-7 6x+3=8x-7 6x-8x=-7-3 -2x=-10 -x=-10/2 -x=-5 x=5 d) 23-7x=42x-107 -7x-42x=-107-23 -49x=-130 -x=-130/49 x=130/49 e) 8(x-2)-3x=4(x+3)-5 8x-16-3x=4x+12-5 8x-3x-4x=12-5+16[…]
21 mai 2009 ∙ 1 minute de lecture
Quelques Applications sur les Fonctions Affines
Comment calculer une image ? Rappels Une fonction linéaire est un cas particulier d'une fonction affine. L'équation d'une fonction affine est de la forme : f(x)=ax+b et L'équation d'une fonction linéaire est de la forme : f(x)=ax+b=ax (car b=0) Je rappelle également que : « a » est appelé coefficient directeur de la droite ou[…]
21 mai 2009 ∙ 2 minutes de lecture
La Résolution d’un Système par Substitution
Comment faut-il procéder ? Résoudre le système suivant {x+4y-4=0 {2x-y=0 Etape 1 On isole l'une des inconnues à gauche d'une des équations (ici, on décide par exemple d'isoler « x » à gauche, dans la première équation). {x=-4y+4 {2x-y=0 Etape 2 Dans la deuxième équation, on remplace « x » par sa valeur en «[…]
21 mai 2009 ∙ 1 minute de lecture
Résolution par Combinaison Linéaire
Comment utiliser cette méthode ? Cette méthode, également appelée méthode par addition, consiste à éliminer une des inconnues par addition des deux équations en cours de math. Résoudre les deux systèmes suivant 1) {2x+y=0 (L1) {4x-5y=-1 (L2) ici L1= Equation n°1 L2= Equation n°2 Solution Etape 1: On choisit par exemple d'éliminer les y. Pour[…]
20 mai 2009 ∙ 2 minutes de lecture
Le PGCD et ses Particularités
Comment le calculer ? Le PGCD de deux nombres entiers a et b est le nombre entier le plus grand qui divise à la fois a et b. On le note PGCD(a;b) Exemple 6 et 10 sont tous les deux divisibles par 2. 2 EST LE SEUL DIVISEUR COMMUN à 6 ET 10 6=2*3; 10=2*5[…]
19 mai 2009 ∙ 1 minute de lecture
Interprétations Graphique d’un Système
Comment les interpréter ? Interprétation graphique d'une équation à deux inconnues Toute équation de la forme : ax+by+c=0 est une équation cartésienne d'une droite. Exemple : 2x+3y=5 Cette équation peut être mise sous forme réduite, et on obtient alors y=-(2/3)x+(5/3) On retrouve donc bien la forme usuelle de l'équation de droite (fonctions affines) Donc tous[…]
11 mai 2009 ∙ 2 minutes de lecture
Repères et Coordonnées
Comment les tracer ? Repère Un repère est formé de deux axes gradués sécants entre eux, et d'un point O appelé origine du repère, situé à l'intersection des deux axes. Repère orthogonal Quand les axes du repère sont perpendiculaires, on dit que le repère est orthogonal. L'axe horizontal est appelé axe des abscisses, et noté[…]
11 mai 2009 ∙ 2 minutes de lecture
Problèmes avec Mise en Equation
Comment trouver la solution ? Le problème en question -Lors de la fete des meres , un enfant offre une eau de toilette qui coute 25€ et un bouquet de roses , chaque rose coutent 1,60€ . Il en a en tout pour 39,40€ *Combien de roses a-t-il offert ? Tout d'abord nous devons determiner[…]
9 mai 2009 ∙ 1 minute de lecture
Les Hypothèses de Thalès
Comment ce théorème est-il né ? Présentation Le théorème de Thalès, dans le triangle. Tu connais. J'en suis sûr. Non ? Mais si, mais si ! le théorème de Thalès... celui que tu as vu en quatrième. Je reviendrai sur son énoncé si vraiment tu ne vois toujours pas de quoi il s'agit. Il n'a[…]
8 mai 2009 ∙ 4 minutes de lecture
Polygones Réguliers
Comment les différencier ? Définition Un polygone régulier est un polygone dont tous les côtés ont la même longueur et tous les angles ont la même mesure. Propriétés a) Cercle circonscrit et polygone régulier Pour tout polygone régulier, il existe un cercle C passant par tous les sommets du polygone, et de centre O. Ce[…]
5 mai 2009 ∙ 2 minutes de lecture