
Cours de Mathématiques : la Racine Carrée
Définir le radical d'un nombre I. Racine carrée 1) Définition Pour tout nombre positif a, la racine carrée de a est le nombre positif dont le carré est égal à a. Exemple : La racine carrée de 64 est 8 parce que 82 = 64 et 8 ≥ 0. La racine carrée de a se[…]
13 décembre 2006 ∙ 2 minutes de lecture

Les Inéquations en Mathématiques
Propriétés et usages des inégalités I. Définition Une inégalité dans laquelle un nombre inconnu est remplacé apr un lettre s'appelle une inéquation. Résoudre une équation, c'est trouver toutes les valeurs numériques que l'on peut donner à cette inconnue pour que l'inégalité soit vraie. II. Propriétés des inégalités Soit trois nombres a, b et c :[…]
13 décembre 2006 ∙ 2 minutes de lecture

Sujet du Brevet de Maths 2005 : Histogrammes
Épreuve sur les statistiques des notes Exercice Voici l'histogramme des notes d'un contrôle noté sur 5 pour une classe de 25 élèves. 1 ) Reproduire et remplir le tableau des notes suivants. 2) Calculer la moyenne des notes de la classe ? 3) Quelle est la médiane des notes de la classe ? 4) Calculer la fréquence[…]
11 décembre 2006 ∙ 2 minutes de lecture

Exercice Corrigé du Brevet sur la Racine Carrée
Extrait de l'examen sur les radicaux Écrire B sous la forme a √5 , où a est un entier relatif. B = √45 - 12√5 B = √(9 x 5) - 12√5 = √9 x √5 - 12√5 = 3√5 - 12√5 = (3 - 12) √5 = - 9 √5
11 décembre 2006 ∙ 1 minute de lecture

Exercice du Brevet de Mathématiques sur les Fractions
Annales de l'épreuve avec correction Énoncé Soit A = 5/3 – 7/3 x 9/4 Calculer A et donner le résultat sous la forme d'une fraction irréductible. Corrigé A = 5/3- (7 x 9) / (3 x 4) = 5/3- 63/12 = (5 x 4) / (3 x 4)- 63/12 = 20 / 12- 63/12 =[…]
11 décembre 2006 ∙ 1 minute de lecture

Extrait du Brevet de Mathématiques de 2005
Exercice de calcul de l'examen Exercice Dans cet exercice, tous les calculs devront être détaillés. 1) Calculer l'expression : A = 13/3- 4/3 x 5/2 (donne le résultat sous sa forme la plus simple). 2) Donner l'écriture scientifique du nombre B tel que : B = (7 x 1015 x 8 x 10 -8) / 5 x[…]
11 décembre 2006 ∙ 1 minute de lecture

Entraînement au Brevet de Mathématiques
Question et corrigé type de l'examen de calculs Soit D = ( 2x + 7)2 + ( 2x + 7 ) ( x - 2 ). 1) Développer et réduire D Pour développer D on utilise d'une part l'identité remarquable (a + b) 2 = a2 + 2ab + b2 et d'autre part (a +[…]
26 novembre 2006 ∙ 2 minutes de lecture

Propriétés du Théorème de Thalès
La formule des parallèles traversant le triangle Soient -d et d' deux points secantes en A -B et M deux points de d, distincts de A -c et n deux points de d', distincts de A Si les droites (BC) et (MN) sont paralléles, alors AM sur AB= AN sur AC[…]
22 novembre 2006 ∙ 1 minute de lecture

Exercice et Corrigé du Brevet de Maths en 2005
Développer ou factoriser des équations On considère l'expression E = 4x2 - 9 + (2x + 3)( x - 2). 1. Développer et réduire l'expression E E = 4x2 -9 + 2x * x +2x * (-2) + 3 * x + 3 * (-2) E = 4x2 -9 + 2x2 - 4x + 3x[…]
19 novembre 2006 ∙ 2 minutes de lecture

Exercices de Factorisation et de Développement au Brevet
Conseils pour la résolution des calculs algébriques Ils sont tous faits sur le même principe. On donne une expression à : - développer et réduire - à factoriser. Ensuite il y a une équation produit nul à résoudre, en général, c'est la forme factorisée trouvée dans l'exercice (cela permet de vérifier). Et puis il faut[…]
17 novembre 2006 ∙ 1 minute de lecture

Les Questions de Mathématiques au Brevet
Exercice type de l'examen final du collège Énoncé On considère l'expression : A = x2 - 25 - 3( 5 - x )( x + 1 ) + 2( x - 5)2 1. Dévelloper puis réduire A 2. Factoriser au maximun A 3. Résoudre les équations A = 10 ; A = 0 ; A[…]
14 novembre 2006 ∙ 3 minutes de lecture

Annale du Brevet des Collèges de Mathématiques de 2004
Exercice de calcul de l'épreuve de maths Énoncé On donne E = (2x - 3)(x + 2) - 5 (2x - 3) 1. Développer et réduire E. 2. Factoriser E. 3. Calculer E pour x = -2 4. Résoudre l'équation (2x - 3)(x - 3) = 0. Corrigé 1°) Développer et réduire E E =[…]
14 novembre 2006 ∙ 2 minutes de lecture

Exercice Corrigé du Brevet 2006
Comment réussir cet exercice ? E = (3x + 2)2 – (5 - 2x) (3x + 2) Développer et réduire E E = (3x)2 + 2*3x*2 + 22 - (5 * 3x + 5 * 2 - 2x * 3x - 2x * 2) on utilise l'identité remarquable (a + b)2 = a2 - 2ab +[…]
12 novembre 2006 ∙ 2 minutes de lecture

Exercice de Type Brevet
Qu'st-ce qu'une identité remarquable ? Cet exercice s'inspire d'un exercice donné au brevet. A = (2x - 5)2 - (4x + 9) (2x - 5) Développer et réduire A A = 4x2 – 20x + 25 – (8x 2 – 20x + 18x - 45) On utilise l'identité remarquable (a – b)2 et le développement[…]
11 novembre 2006 ∙ 2 minutes de lecture
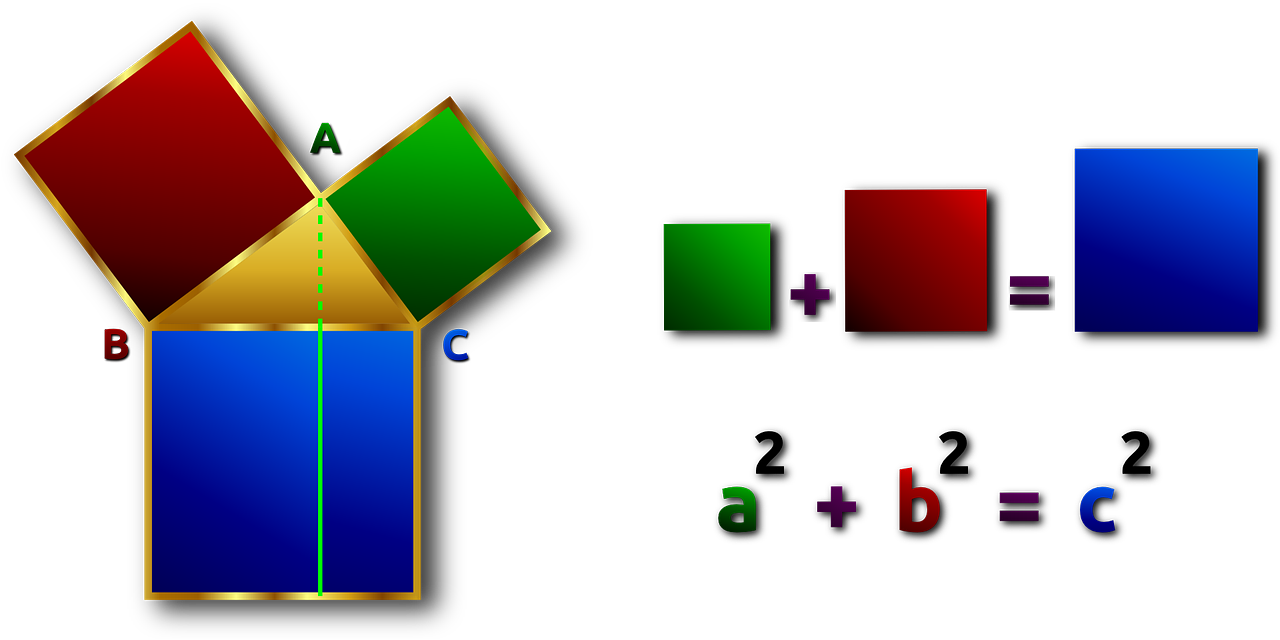
Apprendre le Théorème de Pythagore
Comment l'appliquer ? A quoi sert-il ? Il sert à calculer la longueur d'un côté d'un triangle. Quand l'utiliser ? On peut l'utiliser quand on a un triangle rectangle, et que l'on connaît la longueur de deux des côtés de ce triangle. Énoncé du théorème Dans un triangle rectangle, le carré de la longueur de l'hypoténuse[…]
28 octobre 2006 ∙ 2 minutes de lecture

Rappels sur les Puissances
Comment calculer un nombre au carré ? Les puissances mettre un nombre a la puissance 2, cest le multiplier par lui meme mettre un nombre a la puissance 3, cest le multiplier par lui mem et encore par lui meme mettre un nombre a la puissance 4, cest le multiplier 3 fois par lui meme[…]
10 octobre 2006 ∙ 2 minutes de lecture

Les Équations Produit Nul
Comment les résoudre ? Définition Les lettres a, b, c et d désignent des nombres avec a et c non nul. Une équation produit nul est une équation de la forme : (ax + b) (cx + d) = 0. Propriété Si l'un au moins des facteurs est nul alors le produit est nul. Si A[…]
24 septembre 2006 ∙ 2 minutes de lecture

Exercice sur les Équations Produit Nul
Comment pouvez-vous les résoudre ? Exercices Résoudre les équations : (x + 4) ( x2 - x) = 0 16 x 2 - 25 x = 0 16 x 2 - 20 x + 25 = 0 avant de faire ces exercices, allez vérifier le cours en cliquant ici. Corrigé : on applique la propriété[…]
23 septembre 2006 ∙ 1 minute de lecture

Équations Produit Nul
Qu'est-ce que ce type de calculs ? Définition C'est une équation du type (a x + b) ( c x + d) = 0 c'est à dire le produits de deux expressions du premier degré à une inconnue. Comment la résoudre ? On utilise la propriété suivante : si un produit de facteurs est nul ,[…]
23 septembre 2006 ∙ 1 minute de lecture

Les Égalités Remarquables
Quelles sont-elles ? Première formule Expression mathématique : ( a + b ) 2 = a 2 + 2 a b + b 2 Expression littéraire : Le carré de la somme de deux termes est égal à la somme des carrés de ces deux termes augmentée du double produit des deux termes. Exemple :[…]
22 septembre 2006 ∙ 1 minute de lecture

S’exercer sur les Factorisations
Comment comprendre cette notion ? Exercices Quelques exercices sur la factorisation Factorise les expressions : - (2x + 5)2 - (4x + 6)2 = ? - 4 (3x + 1)2 - (3x +3)2 = ? - 16 - (4x + 5)2= ? - (4 + 5 x)2 - 49 = ? Corrigés Pour tous ces exercices,[…]
20 septembre 2006 ∙ 1 minute de lecture

Exercices sur les Inéquations
Comment choisir le bon pain ? Résoudre une inéquation Résoudre l'inéquation Résoudre un problême Un pain aux noix coûte 0,20 € de moins qu'un pain bûcheron. Avec un billet de 20 €, Sabrina a pu acheter 6 pain aux noix et 9 pains bûcherons. Trouver les prix possibles d'un pain aux noix, sachant qu'il coûte[…]
2 septembre 2006 ∙ 1 minute de lecture

Exercices sur l’Arithmétique
Comment diviser ? Déterminer si deux entiers sont premiers entre eux a) On applique les critères de divisibilité (par 2, par 3, par 5, etc.) pour rechercher les diviseurs de chaque nombre. Ici, la somme des chiffres de 927 et de 225 est divisible par 9, donc ces nombres sont divibles par 9. Ils ont[…]
1 septembre 2006 ∙ 1 minute de lecture

Méthode de Factorisation
Comment s'y prendre ? Rappel Soit a, b et k trois nombres quelconques non nuls. On factorise une expression en transformant une somme en produit. La propriété de distributivité est : ak + bk = k (a + b). Exemples
29 août 2006 ∙ 1 minute de lecture

Pi
π I. Définition Le nombre pi, noté par la lettre grecque du même nom π (Π en majuscule) est le rapport constant entre la circonférence d'un cercle et son diamètre. Il est appelé aussi la constante d'Archimède. Pi est un nombre irrationnel, c'est-à-dire qu'il n'est pas le rapport de deux nombres entiers naturels. L'irrationalité de[…]
14 juin 2006 ∙ 2 minutes de lecture
