Chapitres
- 01. A quoi sert-il ?
- 02. Quand l'utiliser ?
- 03. Énoncé du théorème
- 04. Applications

A quoi sert-il ?
Il sert à calculer la longueur d'un côté d'un triangle.
Quand l'utiliser ?
On peut l'utiliser quand on a un triangle rectangle, et que l'on connaît la longueur de deux des côtés de ce triangle.
Énoncé du théorème
Dans un triangle rectangle, le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.
Ainsi, si ABC est rectangle en A, l'hypoténuse est BC et donc on a :
BC² = AB² + AC²
Applications
L'énoncé est écrit en bleu, la correction attendue en noir, les explications en violet et entre parenthèses.
1) EGF est un triangle rectangle en G. EG =3 cm et GF =4 cm. Calculer EF.
EFG est un triangle rectangle en G.
(Le triangle est rectangle et on connaît la mesure de deux de ses côtés, on peut donc appliquer le théorème de Pythagore).
D'après le théorème de Pythagore, on a :
EF² = EG² + GF²
( On pense à bien identifier l'hypoténuse, le triangle est rectangle en G donc on doit retrouver la lettre G deux fois dans la somme).
( A présent, on peut remplacer les longueurs connues : on remplace EG par 3 et GF par 4).
EF² = 3² + 4²
EF² = 9 + 16
EF² = 25
(Petit rappel : 7² = 7 x 7 et non pas 7 x 2...)
EF = racine carrée de 25
EF = 5 cm
1) EGF est un triangle rectangle en G. EF = 10 cm et GF =6 cm. Calculer EF.
EFG est un triangle rectangle en G.
(Le triangle est rectangle et on connaît la mesure de deux de ses côtés, on peut donc appliquer le théorème de Pythagore).
D'après le théorème de Pythagore, on a :
EF² = EG² + GF²
( On pense à bien identifier l'hypoténuse, le triangle est rectangle en G donc on doit retrouver la lettre G deux fois dans la somme).
( A présent, on peut remplacer les longueurs connues : on remplace EF par 10 et GF par 6).
10² = EG² + 6²
100 = EG² + 36
100 - 36 = EG²
64 = EG²
EG² = 64
EG = racine carrée de 64
EG = 8 cm
Petites remarques :
1. Il peut être utile de revoir la simplification des racines carrées, car elle peut être demandée.
2. On peut demander de donner la valeur exacte de la longueur cherchée, ou une valeur approchée.
Si on demande la valeur exacte, on devra conserver l'expression avec une racine carrée si la valeur donnée par la calculatrice contient beaucoup de chiffres après la virgule.
Si on demande une valeur approchée, il faut se rappeler les règles pour arrondir et ce que signifie une valeur approchée à l'unité, au dixième.
Résumer avec l'IA :
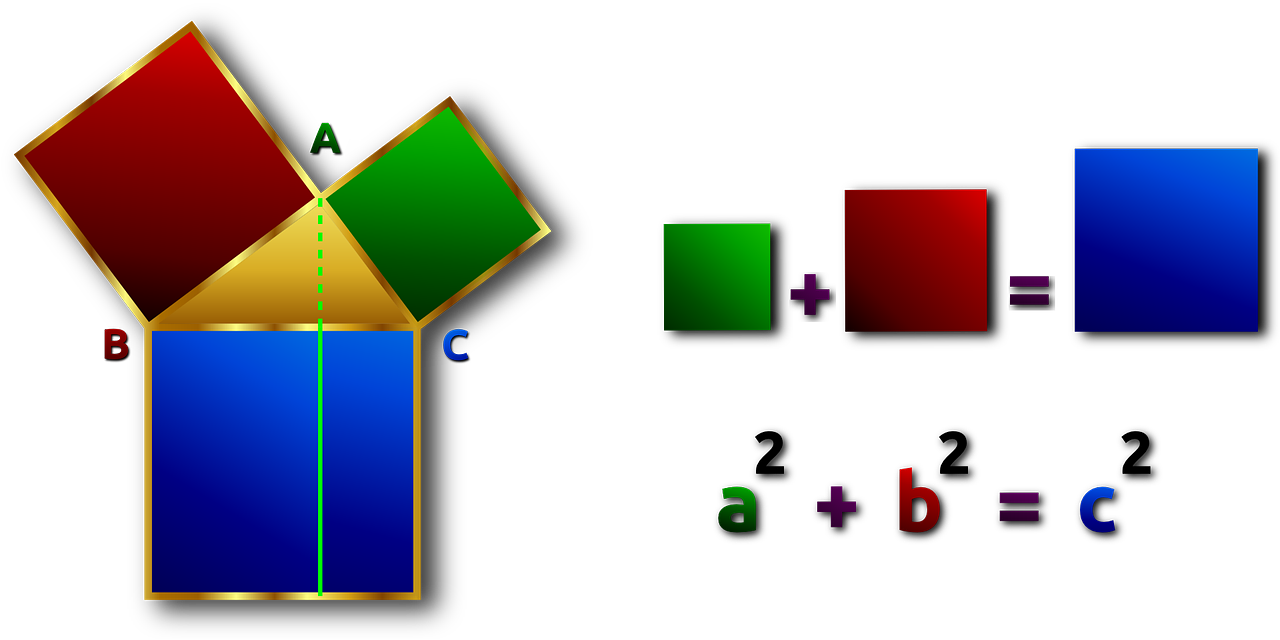






















Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Merci beaucoup pour ces bonnes explications je suis en CM1 et j ai pas mal compris bref merci
Merci beaucoup J’avoue que je décrochais un peu en ce moment et maintenant sa va mieux, le cours est génial.
merci beaucoup ça m’a beaucoup aidé 1000 fois merci
bravo!! =)
Très bon document !
[color=red]Je connais déjà cette leçon par coeur . J’aime bien la façon dont il est rédigé .
C’est un bon document pour apprendre ! [/color]
Ce document m’a bien été utile car maintenant j’ai mieux compris le théorème de pytagore alors qu’avant j’avait des problème avec ça