Chapitres
Le triangle rectangle est plus qu'un simple triangle. En mathématiques, il s'agit de l'une des bases de la géométrie euclidienne et un outil utile pour comprendre le monde qui nous entoure.
Depuis la construction des pyramides en Égypte jusqu'aux charpentes de nos maisons actuelles, la figure du triangle rectangle est omniprésente. Dans les études de mathématiques, il sert de porte vers la trigonométrie. En physique, il permet de décomposer des forces.
Mais pourquoi cette figure est-elle si fondamentale ? Parce qu'elle incarne la stabilité parfaite : l'angle droit représente la rencontre de la verticale et de l'horizontale, celle du mur qui tient debout face à la gravité. Pourtant, son utilité dépasse largement la simple maçonnerie. Aujourd'hui, le triangle rectangle est le moteur invisible de technologies de pointe. De la triangulation utilisée par les satellites GPS pour vous localiser, jusqu'aux calculs de polygones pour l'affichage 3D des jeux vidéo, il est partout. Maîtriser ses secrets, c'est donc s'offrir une clé de lecture universelle dans de nombreux domaines.
Dans cet article, nous allons décortiquer le triangle rectangle, une figure essentielle. Nous passerons sur sa définition précise, ses propriétés uniques et les formules à connaître pour travailler avec les triangles rectangles. Nous verrons enfin ses applications concrètes dans notre quotidien.


Qu’est-ce qu’un triangle rectangle ?
Définition du triangle rectangle
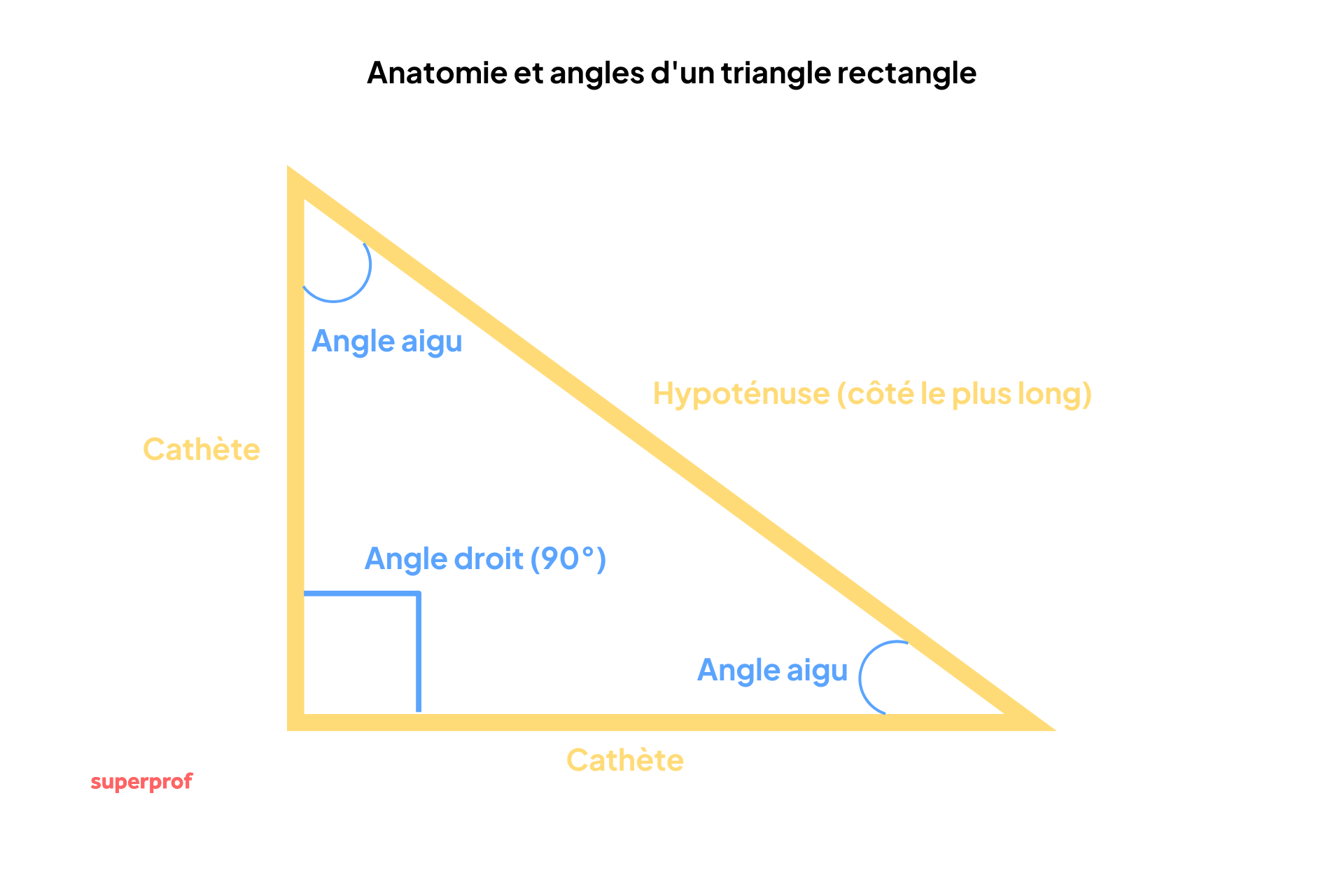
Pour comprendre la figure géométrique du triangle rectangle, il faut commencer par sa définition et son anatomie.
Un triangle rectangle, comme son nom l'indique, est un triangle qui possède une caractéristique particulière : l'un de ses trois angles est un angle droit (de 90°).
Au niveau de ses côtés, ils portent tous un nom particulier : le côté directement opposé à l'angle droit est l'hypoténuse et il s'agit du côté le plus long du triangle rectangle. Les deux autres côtés sont appelés les cathètes, ils sont adjacents à l'angle droit et forment un "L" perpendiculaire autour de l'angle droit.
Propriétés géométriques du triangle rectangle
Les triangles rectangles ont des propriétés bien particulières. Ces dernières sont dites immuables car elles sont toujours vraies quelle que soit la taille du triangle.
L'une des propriétés principales est la complémentarité des angles aigus. C'est une propriété très utile en arithmétique. Cette dernière indique que la somme des trois angles de n'importe quel triangle est égale à 180°. Puisque le triangle rectangle a déjà un angle de 90°, il ne reste que 90° à se partager entre les deux autres angles aigus du triangle rectangle. Les deux angles aigus sont donc complémentaires : leur somme est toujours égale à 90°. Connaître la mesure de l'un des angles aigus permet de calculer automatiquement l'angle de l'autre.
Une autre propriété fondamentale est celle de la suprématie de l'hypoténuse. Elle dit que l'hypoténuse est toujours le côté le plus long d'un triangle rectangle. Comme l'angle droit (90°) est nécessairement le plus grand angle du triangle, le côté qui lui fait face (l'hypoténuse) est mathématiquement le plus grand.
Pour finir, le triangle rectangle est la base à deux autres grandes règles des mathématiques : le théorème de Pythagore et la trigonométrie. Le premier permet de relier les longueurs des côtés entre elles et le second permet de relier les mesures des angles et des côtés des triangles grâce aux sinus, cosinus et tangentes.

Les différents types de triangles rectangles
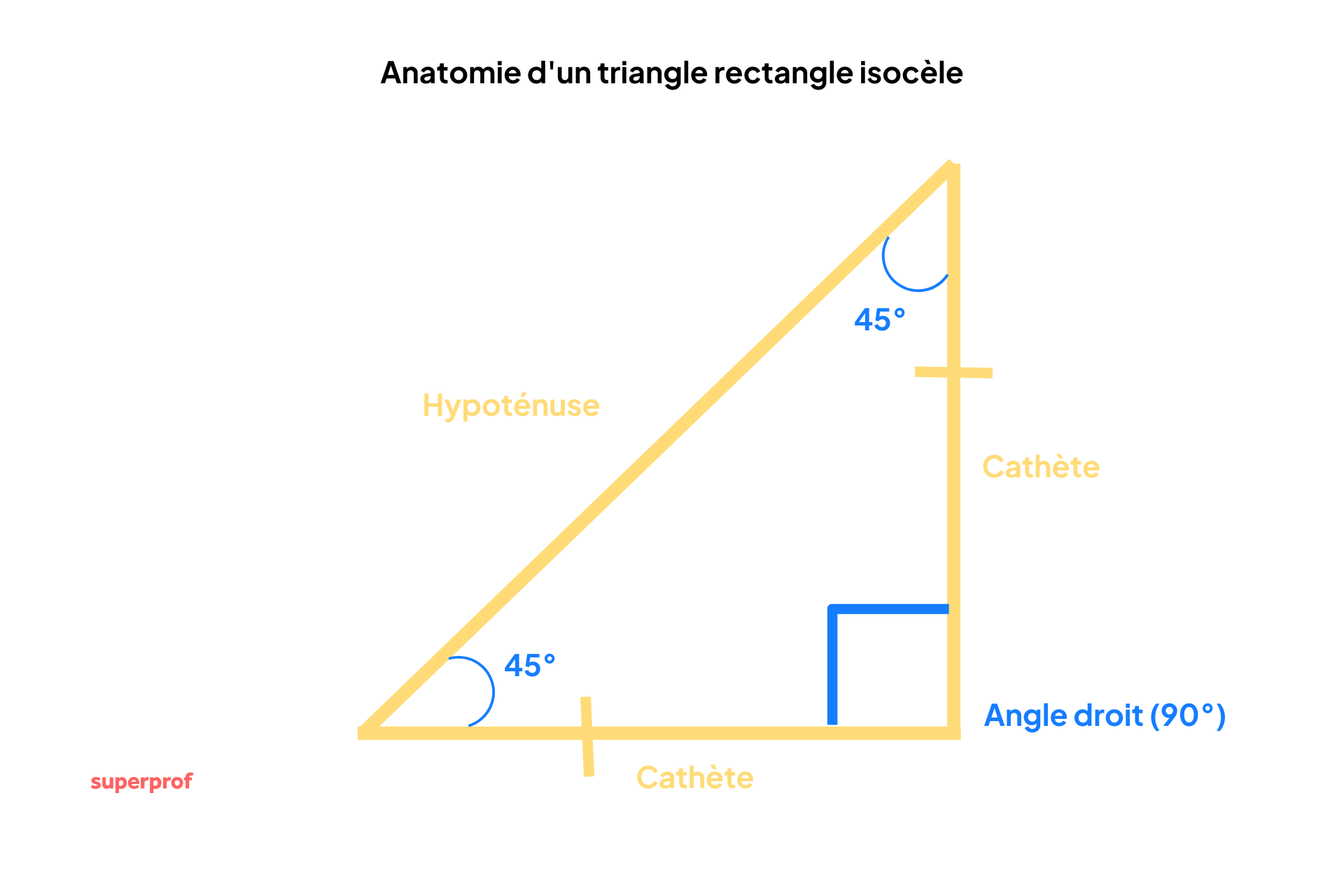
Le triangle rectangle isocèle
Tous les triangles rectangles ont un angle de 90°, comme nous l'avons vu précédemment. Cependant, certains possèdent des caractéristiques supplémentaires. C'est le cas du triangle rectangle isocèle. On l'appelle aussi demi-carré. Voici ses caractéristiques :
- Un angle droit ;
- Deux côtés de même longueur (les cathètes) ;
- Deux angles de 45°.
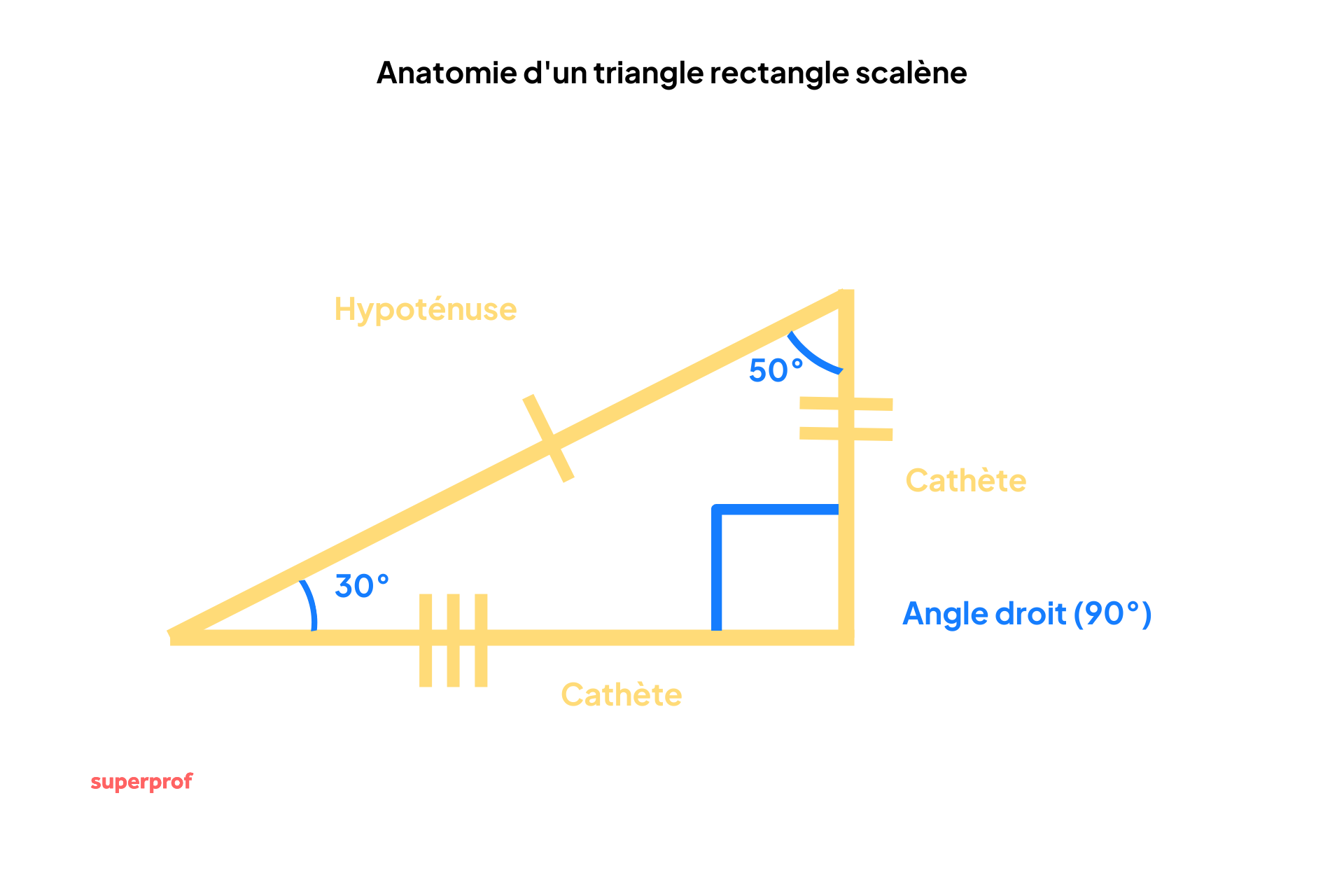
Le triangle rectangle scalène
Un autre triangle rectangle remarquable est le triangle rectangle scalène. Par opposition au triangle rectangle isocèle, le triangle rectangle scalène n'a pas de mesures identiques, pas d'angles de même mesures. Il s'agit du triangle rectangle standard que vous risquez de croiser le plus souvent.
Voici les caractéristiques qui le définissent :
- Ses 3 côtés sont de longueurs différentes ;
- Pas de symétrie ;
- Tous ses angles sont de mesures différentes.
Comment savoir si un triangle est rectangle ?
Face à un triangle quelconque, il est parfois difficile de dire à l'oeil nu si un triangle est rectangle. C'est pourquoi les mathématiques nous fournissent des outils. Le théorème de Pythagore et les fonctions trigonométriques en font partie.
Le théorème de Pythagore
Énoncé du théorème de PythagoreDans un triangle, si le carré de la longueur du plus grand côté est égal à la somme des carrés des longueurs des deux autres côtés, alors ce triangle est rectangle.
À l'origine, le théorème de Pythagore sert à mesurer des longueurs. Mais sa réciproque permet facilement de prouver qu'un triangle est rectangle.
Pour vérifier l'égalité énoncée par le théorème, il faut appliquer la formule suivante : a² + b² = c² avec c étant l'hypoténuse.
Prenons un exemple pratique. Soit un triangle dont les côtés mesurent 3 cm, 4 cm et 5 cm.
Voici la méthode :
- On repère le plus grand côté : il s'agit de celui de 5 cm ;
- On calcule son carré : 5² = 25 ;
- On calcule la somme des carrés des deux autres côtés : 3² + 4² = 9 + 16 = 25 ;
- En conclusion : comme 25 = 25, l'égalité est vérifiée, d'après le théorème de Pythagore, le triangle est bien rectangle.
Les fonctions trigonométriques
Quand on ne connaît pas tous les côtés ou que l'information recherchée concerne la mesure d'un angle, alors le théorème de Pythagore ne suffit plus. C'est alors qu'intervient la trigonométrie. Ces règles de mathématiques permettent de naviguer entre les mesures des angles et les longueurs des côtés d'un triangle.
Voici les formules essentielles de la trigonométrie pour un angle aigu donné α dans un triangle rectangle :
- Sinus (sin) : on l'utilise quand on connaît le côté opposé et l'hypoténuse :
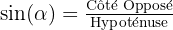
- Cosinus (cos) : on l'utilise quand on a le côté adjacent et l'hypoténuse :
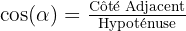
- Tangente (tan) : on l'utilise quand on a le côté opposé et adjacent :
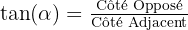

Calculs essentiels du triangle rectangle
Une fois le triangle rectangle identifié, il est souvent nécessaire d'effectuer des calculs. Des formules existent et il est impératif de les connaître. Elles sont utiles par exemple pour mesurer la taille d'une clôture d'un terrain ou encore la bonne quantité de tuiles pour couvrir un toit.
Calcul de l’aire d’un triangle rectangle
L'un des calculs élémentaires est celui de l'aire du triangle rectangle. Cette mesure vous sera utile pour calculer la surface d'une toiture par exemple ou encore effectuer de l'aménagement chez vous (espace sous un escalier notamment).
Comme un triangle rectangle est exactement un rectangle coupé en deux, la formule de calcul de l'aire est la même que celle du rectangle, mais divisé par deux. La formule est la suivante : 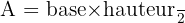 .
.
Calcul du périmètre d’un triangle rectangle
Le calcul du périmètre d'un triangle rectangle correspond à la somme de tous les côtés du triangle. Ces calculs peuvent être utiles pour mesurer la longueur de clôture nécessaire pour engrillager un terrain. Voici la formule permettant de mesurer le périmètre d'un triangle rectangle :  .
.
Calcul des angles d’un triangle rectangle
Dans certains cas, vous connaîtrez les longueurs du triangle mais pas les mesures des angles. Pour faire ces calculs, il faudra utiliser les fonctions inversées de la trigonométrie, déjà vues précédemment.
Voici les formules inversées de la trigonométrie :
- Arcsin (sin-1) : A utiliser si l'on connaît le côté opposé et l'hypoténuse :
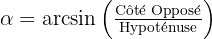
- Arccos (cos-1) : S'utilise si l'on connaît le côté adjacent et l'hypoténuse :
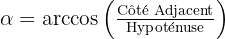
- Arctan (tan-1) : A utiliser si l'on connaît le côté opposé et le côté adjacent :
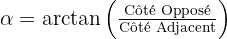
Triangle rectangle : exercices pratiques
Maintenant que vous avez bien appris la théorie, place à la pratique ! Voici quelques exercices pour vous entraîner sur les triangles rectangles et les calculs sur ces derniers.
Énoncé : Soit un triangle ABC rectangle en A. On sait que le côté AB mesure 6 cm et le côté AC mesure 8 cm.
Question : Combien mesure l'hypoténuse (le côté BC) ?
Puisque le triangle est rectangle en A, on peut appliquer le théorème de Pythagore. La formule est : 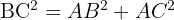
On remplace par les valeurs : 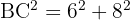
On calcule les carrés : 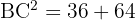
On additionne : 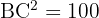
On prend la racine carrée : 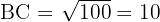
Réponse : L'hypoténuse BC mesure 10 cm.
Énoncé : Un maçon souhaite vérifier si le coin d'un mur est bien perpendiculaire. Il trace un triangle sur le sol avec les mesures suivantes :
- Côté 1 = 100 cm
- Côté 2 = 240 cm
- Diagonale (plus grand côté) = 260 cm.
Question : Le triangle est-il rectangle ?
On utilise la réciproque du théorème de Pythagore. On doit vérifier si le carré du plus grand côté est égal à la somme des carrés des deux autres.
Calcul du plus grand côté au carré : 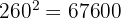
Calcul de la somme des deux autres : 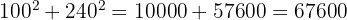
Puisque [67 600 = 67 600, l'égalité est vérifiée. Le triangle est bien rectangle, le mur est donc parfaitement droit.
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Bien
bien mais il y a une erreur pour la tan^b côté opposé/côté adjacent