Chapitres
- 01. Introduction
- 02. Définitions
- 03. Résoudre une équation
- 04. Résoudre une inéquation
- 05. Exercices pour s'entraîner
- 06. Pour aller plus loin
Introduction
Les équations et inéquations sont des égalités et inégalités à une ou plusieurs variables que l'on souhaite résoudre, c'est-à-dire dont on souhaite déterminer les inconnues. Voyons comment les résoudre à l’aide de propriétés et d’exemples.
Une inégalité est une relation entre nombres (ex. 3 + 2 < 5), alors qu’une inéquation contient une inconnue et cherche les valeurs qui rendent l’inégalité vraie (ex. 3 + 2x < 12).
Définitions
Une équation en mathématique est une relation, en général une égalité, comprenant une ou plusieurs variables, aussi appelées des "inconnues". Ce sont ces inconnues que nous allons vouloir déterminer, c'est ce qu'on appelle résoudre l'équation.
En troisième, nous étudierons uniquement les équations à une inconnue. Par exemple, [3x+2=1] où x est l'inconnue à déterminer. On dit que 3x+2 est le membre de gauche et 1 le membre de droite.
Une inéquation fonctionne comme une équation mais au lieu d'une égalité on a une inégalité, c'est-à-dire qu'à la place du signe "=", on trouve les signes "<" (inférieur strict), ">" (supérieur strict) ou encore ≤ et ≥ (inférieur ou égal et supérieur ou égal).
Résoudre une équation
Regardons différents exemples afin de comprendre comment résoudre une équation.
Reprenons [3x+2=1]
Le but va être d'isoler le x d'un côté ou de l'autre afin de déterminer la valeur de x pour laquelle l'égalité est vraie. Pour cela, on passe par différentes étapes :
Dans un premier temps, on souhaite enlever toutes les additions et soustractions présentes dans le membre de gauche, c'est-à-dire dans le membre où se trouve l'inconnue x.
Dans notre équation, on souhaite faire disparaître le "+2" du membre de gauche. Pour cela, on va soustraire 2 à chacun des membres, c'est-à-dire de chaque côté de l'égalité.
[3x+2-2=1-2] ce qui revient à [3x=-1]
Maintenant, on souhaite isoler x, c'est-à-dire que l'on souhaite faire disparaître le 3 présent devant le x. Pour cela, on va diviser par 3 les 2 membres afin que l'égalité reste vraie.
On obtient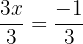 
ce qui revient à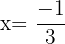 
Donc l'égalité est vraie pour [x=\dfrac{-1}{3}] c'est-à-dire que la solution de l'équation est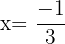
Faisons un deuxième exemple détaillé : [-x+4=-2x+2]
La première étape est d'ajouter 2x des deux côtés pour les regrouper entre eux.
On obtient [-x+4+2x=-2x+2+2x] ce qui équivaut à [x+4=2]
Maintenant, on résout comme précédemment l'équation. On soustrait 4 des deux côtés pour isoler le "x" : [x+4-4=2-4] ce qui revient à [x=-2]
Ainsi, la solution de l'équation est x=-2.
On peut vérifier que l'on ne s'est pas trompé dans la solution en remplaçant x par -2 dans chacun des membres au départ de l'équation :
−(−2) + 4 = 2 + 4 = 6 pour le membre de gauche
−2 × (−2) + 2 = 4 + 2 = 6 pour le membre de droite
On a bien égalité des deux membres donc on a trouvé la bonne valeur.
Ce qu'il faut retenir des exemples :
- Lorsque qu'une addition de deux termes avec des "x" apparaît, on peut les réunir (ex : 2x+3x=5x). Il en est de même pour la soustraction.
- La solution d'une équation à une inconnue est toujours unique, il n'en existe pas d'autre.
- L'égalité reste vraie lorsque l'on additionne ou soustrait les deux membres par un même nombre. On ne peut pas additionner un seul des deux membres : 2x+2=6 ne donne pas le même résultat que 2x=6, mais il donne le même résultat que 2x+2-2=6-2.
- Enfin, de la même façon, l'égalité reste vraie lorsque l'on multiplie ou divise les deux membres par un même nombre.
Résoudre une inéquation
On résout une inéquation de la même manière que l'on résout une équation mais certaines propriétés supplémentaires vont s'appliquer pour la multiplication et la division des deux membres par un même nombre.
En effet, lorsque l'on multiplie ou divise les deux membres par un nombre positif, l'inégalité reste vraie comme avec une équation.
Par exemple, 3x < 2 équivaut à x < 2/3.
Cependant, lorsque l'on multiplie ou divise les deux membres par un nombre négatif, on change le sens de l'inégalité. Par exemple, on sait que 2<3, si on multiplie les deux cotés de l'inégalité par -10, cela fait -20>-30. C'est bien -30 qui est le plus petit donc il faut inverser le sens de l'inégalité.
Représentation graphique des solutions
Pour visualiser les solutions d’une inéquation, on les représente sur un axe gradué :
- Crochets ouverts pour
>ou< - Crochets fermés pour
≥ou≤ - Hachures pour indiquer les parties non solutions
Regardons deux exemples de résolution d'inéquation.
Résolvons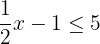 
On souhaite isoler le x. La première étape est de faire disparaître le "-1" du membre de gauche. Pour cela, on ajoute 1 de chaque côté de l'inéquation.
On obtient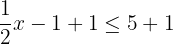 
ce qui équivaut à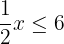 
Ensuite, il faut faire disparaître le facteur situé devant le x afin de déterminer les valeurs de x pour lesquelles l'inéquation est vraie. Pour cela, il nous suffit de multiplier par 2 chacun des membres de l'inégalité. Comme 2 est positif, on ne change pas le sens de l'inégalité.
On obtient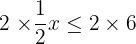 
ce qui revient à écrire [x \leq 12[/latex]
Tous les nombres plus petits que 12 et le nombre 12 sont solutions de l'inéquation. On note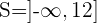 
Prenons un deuxième exemple [-x >2x+9]
Dans un premier temps, il est nécessaire de réunir les x dans un même côté. Passons tous les x à gauche. Pour cela, il faut faire disparaître le "2x" à droite. On va donc soustraire 2x de chaque côté de l'inégalité.
On obtient [-x-2x>2x+9-2x] ce qui revient à [-3x>9]
On doit alors diviser par -3 de chaque côté de l'inéquation pour isoler le x. Cela implique que l'on doit changer le sens de l'inégalité.
On obtient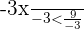 
ce qui donne finalement [x<-3]
Donc les solutions de l'inéquation sont l'ensemble des x strictement inférieur à -3.
Les règles à retenir sont :
- On peut additionner ou soustraire les termes possédant des "x" comme pour les équations. Par exemple, 2x-3x=-x.
- L'inégalité reste vraie lorsque l'on additionne ou soustrait les deux membres par un même nombre.
- L'inégalité reste vraie lorsque l'on multiplie ou divise les deux membres par un même nombre positif.
- On change le sens de l'inégalité lorsque l'on multiplie ou divise les deux membres par un même nombre négatif.
- Une inéquation possède un ensemble de solutions et non une unique solution comme l'équation.
| Opération | Effet sur l’inéquation | Exemple |
|---|---|---|
| Ajouter ou soustraire un nombre aux deux membres | Inéquation inchangée | ax + b > c → ax > c - b |
| Multiplier/diviser par un nombre positif | Inéquation inchangée | ax > b ; a > 0 → ax > b |
| Multiplier/diviser par un nombre négatif | Changement de sens | -ax > b → x < -b/a |
Exercices pour s'entraîner
Résoudre les équations suivantes :
- [3x+1=4]
- [x+6=5x-2]
- [-4x+5=1-2x]
Affichons les résultats dans un tableau :
| Equation | Etape 1 | Etape 2 | Solution |
|---|---|---|---|
| 3x+1=4 | 3x=3 | x=1 | x=1 |
| x+6=5x-2 | -4x+6=-2 | -4x=-8 | x=2 |
| -4x+5=1-2x | -2x+5=1 | -2x=-4 | x=2 |
Résoudre les inéquations suivantes :
- [-2x<6]
- [3x+3>-6x-9]
- [-5x+2<-x]
Affichons les résultats dans un tableau :
| Inéquation | Etape 1 | Etape 2 | Solution |
|---|---|---|---|
| -2x<6 | -2x/-2>6/-2 | x>-3 | x>-3 |
| 3x+3>-6x-9 | 9x+3>-9 | 9x>-12 | x>-12/9=-4/3 |
| -5x+2<-x | -4x+2<0 | -4x<-2 | x>-2/-4=0,5 |
Pour aller plus loin
Il existe de nombreuses équations plus compliquées que l'on sait résoudre. L’ensemble solution est souvent un intervalle.
En classe de seconde, on apprend à résoudre les équations polynomiales du second degré c'est-à-dire des équations de la forme [ax^2+bx+c=0] où a,b et c sont des nombres connus. On apprend également à résoudre les inéquations avec des polynômes du second degré.
On apprend également à résoudre les systèmes de deux équations à deux inconnues, par exemple :
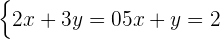
Différentes méthodes existent pour les résoudre : la méthode par substitution et la méthode par combinaison.
Enfin, en classe de terminale, on verra les équations différentielles simples. Ce sont des équations qui possèdent une inconnue x et sa dérivée x'.
Vous avez aimé cet article ? Notez-le !
Loading...
Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Je veux devenir grand mathématiciens