Chapitres
Introduction
Le rectangle est un quadrilatère particulier que nous connaissons tous. Connu pour ses angles droits et ses côtés opposés parallèles, il possède de nombreuses propriétés qu'il est nécessaire de connaître et de savoir utiliser.
Définition et propriétés d’un rectangle
Qu’est-ce qu’un rectangle ?
Par définition, un rectangle est un quadrilatère dont les côtés consécutifs sont perpendiculaires, c'est-à-dire que tous ses angles sont droits, qu'ils mesurent tous 90°. C'est un polygone à quatre côtés, c’est-à-dire une figure fermée possédant 4 côtés et 4 angles droits. Le rectangle possède donc 4 sommets et 4 côtés.
Propriétés générales du rectangle
Le rectangle est un parallélogramme particulier et possède donc toutes les propriétés du parallélogramme, c'est-à-dire que les côtés opposés sont parallèles et de même longueur, les angles opposés sont de même mesure, les diagonales se coupent en leur milieu et leur point d'intersection est le centre du parallélogramme, c'est le centre de symétrie.
On appelle la longueur du rectangle la longueur des côtés les plus grands. De même, on nomme la largeur du rectangle la longueur des côtés les plus petits.
En plus des propriétés du parallélogramme, le rectangle en recense quelques autres :
Ces quatre angles sont des angles droits.
Il possède deux axes de symétrie qui sont les médiatrices des côtés et qui se coupent au milieu du rectangle.
Il a ses diagonales de même longueur.
Les diagonales, étant de même longueur et se coupant en leur milieu en un point noté O, font que les quatre sommets du rectangle sont équidistants de ce point. Ainsi il existe un cercle de centre O passant par ces quatre sommets, appelé cercle circonscrit au rectangle, on dit que le rectangle est inscrit dans le cercle.
| Propriété | Description |
|---|---|
| Angles | Tous droits (90°) |
| Côtés opposés | Parallèles et de même longueur |
| Diagonales | Égales et se coupent en leur milieu |
| Axes de symétrie | 2 (médianes des côtés) |
| Particularité | Un carré est un rectangle avec tous les côtés égaux |
Le carré : un rectangle particulier
Un rectangle particulier est le carré : c'est un rectangle dont les côtés sont tous de même longueur. Cela implique de plus que les diagonales se coupent perpendiculairement.
Où trouver des cours de maths pour réviser avant une épreuve ?
Comment construire et reconnaître un rectangle
Construction avec règle et équerre
On veut construire un rectangle ABCD de longueur L et de largeur l à l'aide d'une règle graduée et d'un équerre.
On trace un segment [AB] de longueur L. On trace à l'aide d'une équerre, le segment [AD] de longueur l, perpendiculaire au segment [AB] et passant par A. On trace de la même façon le segment [DC] de longueur L, perpendiculaire au segment [AD] et passant par D. Enfin on relie les points C et B et on vérifie que les angles sont bien tous droits.
Construction avec les diagonales
Il est également possible de tracer un rectangle en traçant ses diagonales : deux segments de même longueur et se coupant en leur milieu. Il ne reste alors qu'à relier les points pour obtenir le rectangle.
Méthodes pour identifier un rectangle
Il y a plusieurs solutions pour déterminer si un quadrilatère est un rectangle.
La première est grâce à ses angles.
Si un quadrilatère a trois angles droits alors c'est un rectangle.
On peut également déterminer si un quadrilatère est un rectangle à partir d'un parallélogramme :
Si un parallélogramme a un angle droit alors c'est un rectangle.
La deuxième possibilité est par ses diagonales.
Si un quadrilatère a ses diagonales qui ont la même longueur et qui se coupent en leur milieu alors c'est un rectangle.
On peut également partir d'un parallélogramme :
Si un parallélogramme a ses diagonales de même longueur alors c'est un rectangle.
Aire et périmètre d’un rectangle
Calcul du périmètre
On note L la longueur du rectangle et l la largeur.
Le périmètre du rectangle est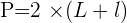 
C'est la longueur que mesure le contour de la figure c'est-à-dire la somme des longueurs des côtés. On le calcule souvent en cm ou m.
Calcul de l'aire
L'aire du rectangle est 
C'est la surface délimitée par le rectangle. Souvent on la calcule en cm² ou m² .
On peut aussi voir le rectangle comme l'addition de deux triangles rectangles de hauteur l et de base L. Ainsi, on obtient bien que l'aire est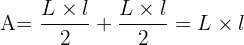 
Exercices sur le rectangle
Pour mettre en pratique ces notions et vérifier votre compréhension, voici une série d’exercices sur le rectangle :
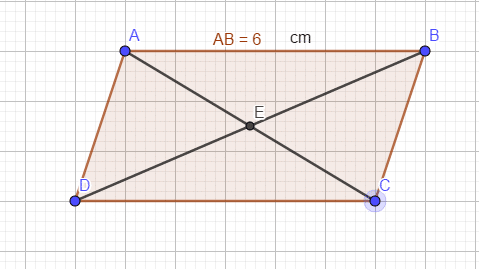
On suppose que AC = DB. Que peut-on en déduire sur la figure et sur le segment [DC] ?
Solution : Si AC = DB, alors les diagonales sont de même longueur. Or, si un parallélogramme a ses diagonales égales, c’est un rectangle. Donc ABCD est un rectangle et AB = DC.
Si AC = DB, alors les diagonales du parallélogramme sont de même longueur. Or, si un parallélogramme a ses diagonales égales, c’est un rectangle. Donc le quadrilatère ABCD est un rectangle. Par conséquent, les côtés opposés sont égaux, donc AB = DC.
On trace un quadrilatère ABCD possédant un angle droit. Si ses côtés opposés sont parallèles deux à deux, que peut-on en déduire ?
Solution : Un quadrilatère avec côtés opposés parallèles est un parallélogramme. Si ce parallélogramme a un angle droit, alors c’est un rectangle. Donc ABCD est un rectangle.
Un quadrilatère ayant ses côtés opposés parallèles est un parallélogramme. Si ce parallélogramme possède un angle droit, alors c’est un rectangle. Donc le quadrilatère ABCD est un rectangle.
Déterminer l’aire et le périmètre des rectangles suivants :
- L = 10 cm et l = 2 cm
- L = 3 m et l = 1000 mm
- L = 9 m et l = 7 m
Conseil : Recenser les réponses dans un tableau et vérifier que toutes les longueurs ont la même unité avant d’additionner ou de multiplier :
| Périmètre | Aire | |
|---|---|---|
| L=10cm et l=2cm | 2(10+2)=2x12=24cm | 10x2=20cm² |
| L=3m et l=1000mm=1m | 2(3+1)=2x4=8m | 3x1=3m² |
| L=9m et l=7m | 2(9+7)=2x16=32m | 9x7=63m² |
- Pour L = 10 cm et l = 2 cm : P = 2 × (10 + 2) = 24 cm ; A = 10 × 2 = 20 cm²
- Pour L = 3 m et l = 1000 mm (1 m) : P = 2 × (3 + 1) = 8 m ; A = 3 × 1 = 3 m²
- Pour L = 9 m et l = 7 m : P = 2 × (9 + 7) = 32 m ; A = 9 × 7 = 63 m²
Vous avez aimé cet article ? Notez-le !
Loading...
Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
👋🏻
👋🏻👋🏻
S’il vous plaît aider moi .
1.a) trace un cercle de centre O et de diamètre 10cm.
b) trace [AC] l’un de ses diamètre et place un point B sur le cercle tel que : mes BAC=53°.
2.a) calcule mes AOB .
b) Deduis-en la mesure de l’angle BOC .
3.a) Calcule la longueur de l’arc AC.
Tu prendras π=3 :
b) [BD] étant un diamètre du cercle , quelle est la longueur de l’arc AD ? Justifié ta réponse .
4.a) Determine les images respectives des points A et B par la symétrie de centre O .
b) Deduis-en la position relative des droites (AD) et (BC) .
5 . Justifie que les angles ADB et CBD ont la même longueur .
il n’y a pas avec les puissants de 10