Chapitres
- 01. Qu’est-ce qu’une fonction ?
- 02. Fonction linéaire : définition et propriétés
- 03. Domaine de définition d’une fonction linéaire
- 04. Comment calculer et représenter une fonction linéaire
- 05. Exemples concrets de fonctions linéaires
- 06. Représentation graphique d’une fonction linéaire
- 07. Exercices corrigés sur les fonctions linéaires

Qu’est-ce qu’une fonction ?
Une fonction est un procédé qui associe à un nombre un autre nombre appelé image. On note généralement la fonction par f, le nombre d'entrée par x et son image par f(x) ou y.
Dans cet article, nous étudions les fonctions linéaires, un type particulier de fonctions où l'image d'un nombre est proportionnelle à ce nombre.
Fonction linéaire : définition et propriétés
Une fonction linéaire de coefficient a est une fonction de la forme :
f(x) = a x
où a est un nombre réel appelé coefficient directeur. Ce coefficient détermine l'inclinaison de la droite :
Caractéristiques principales
- La représentation graphique d'une fonction linéaire est une droite passant par l'origine (0 ; 0).
- Les images et les antécédents sont proportionnels : si on multiplie x par un nombre, f(x) est multiplié par le même nombre.
- Pour trouver l'image d'un nombre, on multiplie par a ; pour trouver un antécédent, on divise par a.
Domaine de définition d’une fonction linéaire
Le domaine de définition d'une fonction représente l'ensemble des nombres pour lesquels la fonction est définie. Par exemple, pour f(x) = 1/x, la division par 0 étant impossible, le domaine est ℝ \ {0}.
Pour une fonction linéaire, le domaine est ℝ, car il n'y a aucune restriction sur x.
Comment calculer et représenter une fonction linéaire
Méthode 1 : Déterminer une fonction linéaire à partir d’un point
Si un point A(x₀ ; y₀) appartient à la droite représentative de f, on peut calculer le coefficient a :
f(x) = a x → a = y₀ ÷ x₀
Exemple : Point A(4 ; 6) :
f(x) = a x
6 = 4 a → a = 6 ÷ 4 → a = 3/2
Donc f(x) = 3/2 x
Méthode 2 : Tracer la droite d’une fonction linéaire pas à pas
La droite passe toujours par l'origine (0 ; 0).
Choisir un second point. On peut prendre une abscisse simple pour simplifier le calcul :
Exemple : g(x) = 2/7 x, choisir x = 7 → g(7) = 2. La droite passe par (0 ; 0) et (7 ; 2).
Placer les deux points sur le graphique et tracer la droite à la règle.
Pour vous entraîner, remplissez le tableau ci-dessous en calculant les images de la fonction f(x) = 2 x pour chaque valeur de x donnée :
| x | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| f(x) |
Méthode 3 : Calculer le coefficient a à partir du graphique
Pour déterminer a à partir d’un graphique :
- Choisir deux points distincts sur la droite : (x₁ ; y₁) et (x₂ ; y₂).
- Calculer : a = (y₂ - y₁) ÷ (x₂ - x₁)
Remarque : il est également possible de relever un point sur la droite et d’appliquer la méthode précédente.
Exemples concrets de fonctions linéaires
Quelques exemples :
- f(x) = 3 x
- g(x) = -2 x
- h(x) = 6,56 x (conversion euros en francs)
- Prix des pommes en fonction du poids : p(x) = 2 x euros
Dans ces situations, la valeur obtenue est proportionnelle à l’entrée.
Représentation graphique d’une fonction linéaire
Les fonctions linéaires se représentent par une droite passant par l'origine :
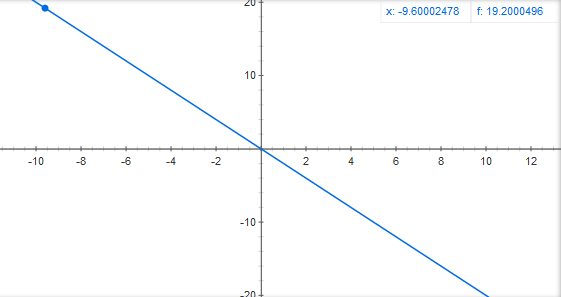
Pour construire la droite, associer chaque valeur de x (abscisse) à son image f(x) (ordonnée) et relier les points.
Exercices corrigés sur les fonctions linéaires
Pour finir, un exercice pour s'entraîner sur les fonctions linéaires :
Calculez l’image ou l’antécédent en utilisant la formule f(x) = a × x.
- Soit f(x) = 3x. Calculez l’image de -1.
- Soit g(x) = -5x. Calculez l’image de 3.
- Soit h(x) = 4x. Trouvez l’antécédent de -1.
- f(-1) = 3 × (-1) = -3
- g(3) = -5 × 3 = -15
- 4x = -1 → x = -1/4
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !