Chapitres
Introduction aux vecteurs
Pour effectuer une translation ou encore pour identifier le coefficient directeur d'une droite, les vecteurs nous offrent de nombreuses applications en géométrie. Commençons par définir ce qu'est un vecteur et étudions ses différentes propriétés et applications.
Qu’est-ce qu’un vecteur ?
Définition d’un vecteur
Un vecteur est un objet mathématique que l'on représente graphiquement sous forme d'une flèche. En effet, un vecteur est défini par sa longueur (longueur du segment), sa direction (position, orientation de la flèche) et son sens (vers la droite ou la gauche).
Caractéristiques : longueur (norme), direction, sens
Sa longueur, appelée norme
Sa direction
Son sens
Il peut être noté de deux façons différentes : soit nous connaissons le point de départ A et le point d'arrivée B et on note le vecteur 
soit nous n'avons aucune information sur le vecteur et nous le notons 
Il est important de ne pas oublier la flèche afin de ne pas confondre avec la longueur du segment. En effet, le vecteur est de longueur AB.
Il est inutile de savoir d'où part un vecteur. Par exemple, les vecteurs et 
ci-dessous sont égaux.
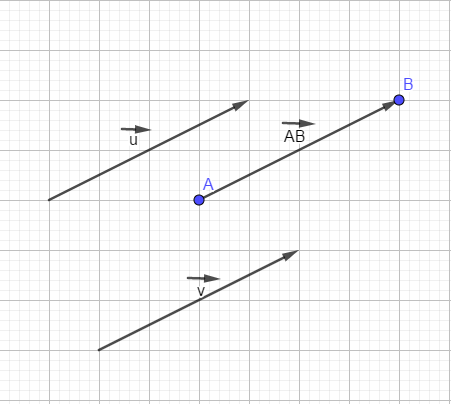
On appelle translation qui transforme A en B le déplacement rectiligne de longueur AB et de direction la droite (AB). En fait, cela correspond au vecteur . On peut dire que représente la translation qui transforme A en B.
Le point B obtenu en appliquant la translation de vecteur est le point qui se trouve au bout du vecteur c'est-à-dire le point à l'extrémité du vecteur lorsque l'origine du vecteur est le point A.
| Caractéristique | Description | Exemple |
|---|---|---|
| Longueur (norme) | Distance entre l’origine et l’extrémité | AB = 5 |
| Direction | Ligne selon laquelle le vecteur agit | Parallèle à x |
| Sens | Vers où pointe la flèche | De A vers B |
| Notation | Comment on écrit le vecteur | , |
Propriétés et types de vecteurs
Vecteur opposé
Le vecteur opposé du vecteur est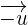 
c'est le vecteur qui a même direction, même longueur mais qui est de sens contraire à De la même façon, le vecteur opposé à est 
ce qui correspond au vecteur 
Tout vecteur 
correspond au vecteur nul. C'est un vecteur, il est donc caractérisé par sa direction, son sens et sa longueur, mais sa longueur est nulle. Deux points confondus définissent également le vecteur nul, noté O.
Addition et soustraction de vecteurs
Pour additionner deux vecteurs, on les met l'un au bout de l'autre, la somme des deux vecteurs est alors le vecteur qui part de l'origine du premier et qui arrive au bout du deuxième.
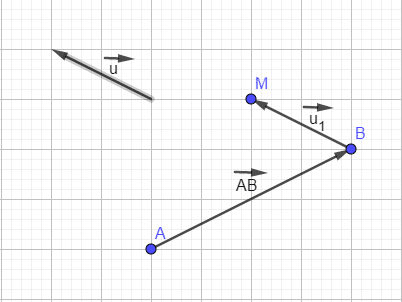
L'addition du vecteur et du vecteur donne le vecteur 
d'après le graphique ci-dessus. On note 
L’addition de deux vecteurs opposés (même direction, sens opposé, même norme) donne le vecteur nul O.
On obtient alors ce qu'on appelle la relation de Chasles, qui permet d'additionner des vecteurs :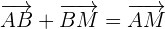 
On a de la même façon la relation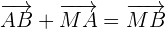 
Pour soustraire deux vecteurs, on additionne le premier avec l'opposé du deuxième, c'est-à-dire on additionne le premier avec le deuxième que l'on a multiplié par (-1) ou encore le deuxième auquel on a inversé le sens.
Multiplication par un scalaire
On peut également multiplier un vecteur par un nombre, par un scalaire. Par exemple, si on multiplie un vecteur par 3 on obtient un vecteur de même direction, de même sens, mais dont la longueur est multipliée par 3. On le notera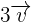 
Deux vecteurs non nuls sont égaux s’ils ont même direction, même sens et même longueur.
Coordonnées et calcul d’un vecteur
Repère orthogonal et repère orthonormé
Avec deux vecteurs perpendiculaires de même origine et de même longueur, on peut former ce que l'on appelle un repère orthogonal. Si de plus, les vecteurs 
et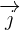 
sont de longueur 1 (ou de norme 1), on dit que le repère est orthonormé. Souvent notée 
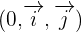c'est le repère que nous utilisons habituellement pour tracer la représentation graphique d'une fonction, comme une droite par exemple. Ainsi, on peut repérer des points dans un plan à l'aide de coordonnées.
Un vecteur a une infinité de représentants : on peut placer l’origine en n’importe quel point du plan.
Coordonnées graphiques d’un vecteur
Graphiquement, les coordonnées d'un vecteur se déterminent en étudiant la distance à parcourir en abscisse et en ordonnée pour aller de l'origine à l'extrémité du vecteur. Ainsi, on regarde en partant de l'origine du vecteur de "combien on avance ou recule" (abscisse du vecteur) et de "combien on monte ou descend" (ordonnée du vecteur) afin d'atteindre le point à l'autre extrémité du vecteur.
Prenons un exemple, en déterminant graphiquement les coordonnées de notre vecteur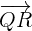 
aussi appelé présent au dessus. En partant de Q, on avance de 3 et on descend de 1 pour arriver à R. Ainsi, le vecteur a pour coordonnées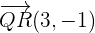 
.
Calcul des coordonnées à partir des points extrémités
Pour calculer les coordonnées d'un vecteur lorsque l'on connait les coordonnées des points aux extrémités du vecteur, on utilise la formule suivante :
Soient A et B des points de coordonnées respectives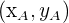 
et 
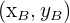Alors
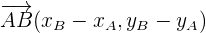
Par exemple, pour le vecteur 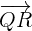on obtient 
Distance entre deux points
On peut calculer la distance entre deux points A et B, notée AB, c'est-à-dire la longueur (aussi appelée la norme) du vecteur La formule est
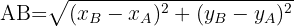
Cela se démontre en appliquant le théorème de Pythagore, où AB est l'hypoténuse.
Calculons la longueur QR. Cela donne 
Milieu d’un segment
On peut également déterminer les coordonnées du point situé au milieu d'un segment. Pour cela, il suffit de calculer la moyenne entre l’abscisse de A et de B et la moyenne entre l'ordonnée de A et de B. On appelle M le milieu du segment AB, cela donne
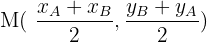
Vecteurs colinéaires
Lorsque deux vecteurs ont même direction (ce qui correspond à "parallèles") on dit que les vecteurs sont colinéaires. Ainsi, deux vecteurs et sont colinéaires s'il existe un nombre k tel que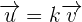 
c'est-à-dire qu'un vecteur est un multiple de l'autre.
Par exemple, les vecteurs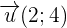 
et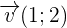 
sont colinéaires car 
Le vecteur nul est colinéaire à tout vecteur. Lorsque les vecteurs et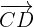 
sont colinéraires, le quadrilatère ABDC est un parallélogramme puisque les segments AB et DC sont parallèles et de même longueur.
Vecteurs et coefficient directeur d’une droite
Définition d’une fonction affine et d’une droite
Pour finir, revenons aux fonctions affines. On sait qu'elles peuvent être représentées dans un repère sous forme d'une droite puisqu'elles ont pour équation y=ax+b où a est le coefficient directeur de la droite et b l'ordonnée à l'origine. On remarque que le coefficient directeur de la droite se mesure graphiquement de la même façon que les coordonnées d'un vecteur.
Calcul du coefficient directeur
En effet, pour le coefficient directeur on regarde en partant d'un point de la droite de "combien on avance ou recule", que l'on note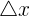 
et de "combien on monte ou descend" 
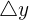afin d'atteindre un autre point de la droite. Le coefficient directeur est alors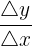 
Vecteur directeur d’une droite
On se demande alors quel est le lien avec les vecteurs ? En fait, le coefficient directeur correspond à la pente de la droite, c'est-à-dire l'inclinaison de la droite, ce qui correspond tout à fait à la définition que nous avons donnée à la direction d'un vecteur. Ainsi, on dira que le vecteur est un vecteur directeur de la droite (AB).
Exercices sur les vecteurs
Voilà quelques exercices pour appréhender les vecteurs !
Déterminer les coordonnées des vecteurs suivants, puis calculer la longueur des segments correspondants :
- A(3;5) et B(4;1)
- A(-4;3) et B(5;2)
- A(6;3) et B(1;-3)
- Utiliser la formule : AB = (xB - xA, yB - yA)
- Calculer la longueur : AB = √((xB-xA)² + (yB-yA)²)
- A(3;5) et B(4;1)
Coordonnées du vecteur : AB = (4-3, 1-5) = (1, -4)
Longueur : AB = √(1² + (-4)²) = √(1 + 16) = √17 - A(-4;3) et B(5;2)
Coordonnées du vecteur : AB = (5-(-4), 2-3) = (9, -1)
Longueur : AB = √(9² + (-1)²) = √(81 + 1) = √82 - A(6;3) et B(1;-3)
Coordonnées du vecteur : AB = (1-6, -3-3) = (-5, -6)
Longueur : AB = √((-5)² + (-6)²) = √(25 + 36) = √61
Pour chaque cas, déterminer si les vecteurs sont égaux ou colinéaires et justifier :
- Soient u(2;4) et v(1;2)
- Vérifier si AB = CD pour que ABDC soit un parallélogramme
- Deux vecteurs sont égaux s’ils ont même direction, sens et norme.
- Utiliser le théorème du parallélogramme pour vérifier l’égalité.
- u(2;4) et v(1;2)
Vérification : 2*v = 2*(1,2) = (2,4) = u → Les vecteurs sont colinéaires. Comme 2*v = u, ils sont également proportionnels. - Vérification AB = CD pour ABDC parallélogramme
Théorème : Les vecteurs AB et CD sont égaux si et seulement si ABDC est un parallélogramme. Vérification : Si les milieux de AD et BC sont les mêmes, alors AB = CD et ABDC est un parallélogramme.
Vous avez aimé cet article ? Notez-le !
Loading...
Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Bonsoir, j’aimerai bien comprendre comment déterminer l’ensemble des points E tels que :le vecteur AE et le vecteur AB soient volontaires. De plus, A B C sont trois points non alignés.
Bonjour je voulais savoir est ce que les composantes d’un vecteur sont toujours en colonnes et celles d’un point sont toujours en lignes? Quelle est la nuance de ces notations