"En mathématiques, le mot "évident" est le mot le plus dangereux." Éric Temple Bell (1883-1960)
En mathématiques, les équations et les inéquations figurent parmi les plus grandes difficultés des élèves. Pour cette raison, Superprof dévoile tout l'univers des équations et inéquations, et surtout ses meilleures astuces pour les résoudre.
Pour résoudre une équation, il faut suivre certaines étapes évidentes :
- Identifier son type
- Appliquer la méthode adaptée (balance, discriminant, factorisation...)
- Vérifier le résultat
- Parfois, reformuler un problème réel en équation
C'est parti pour notre guide concret de mathématiques !

Qu’est-ce qu’une équation et pourquoi c'est difficile ?
En mathématiques comme dans les autres matières, il est nécessaire de comprendre le sens des termes que l’on emploie. Votre prof de maths le dira certainement : saisir la définition du vocabulaire mathématicien est essentiel si l’on veut progresser en maths.
Qu'est-ce qu'une équation ?
Selon le dictionnaire Larousse, l’équation est une « égalité qui n’est vérifiée que pour certaine(s) valeur(s) de la ou des inconnues ».
On ne peut pas faire bien les choses si l'on n'en comprend pas le sens.
Par exemple, on ne peut pas comprendre une fonction asymptotique - celle où toute valeur de f(x) de la droite d'équation x = a s'approche de l'infini, c'est-à-dire quand la valeur de x se rapproche de la valeur finie a aussi près que l'on veut, en restant inférieure ou supérieure à a, mais sans jamais être égale à a - si l'on ne peut se la représenter graphiquement.
Ainsi, avant de faire une équation en mathématiques, on doit en connaître la définition.
Dès cette première définition plutôt généraliste, les termes « valeurs » et « inconnues » apparaissent. Ils ne quitteront pas le processus de résolution de l'équation ou de l'inéquation.
Du reste, ces termes ne quitteront pas non plus le programme de révisions de l'apprenant.
Une équation est donc une relation consistant à trouver les valeurs que peut prendre la variable afin de rendre l'égalité vraie.
Néanmoins, si la notion reste floue, la définition trouvée dans un cours de maths d’une classe de quatrième pourrait mieux convenir, car plus simple : « une équation est une égalité qui comporte une variable (souvent appelée x), elle sert à résoudre des problèmes ».
L'algèbre cherche à résoudre deux familles d'équations :
Les équations polynomiales
Les équations linéaires
Les premières prennent la forme d'une relation de type P(x) = 0, P étant un polynôme.
Les équations linéaires quant à elles, prennent la forme de la relation suivante : a(x) + b = 0. Ici, a est une variable linéaire et b est un vecteur.
L'on a désormais tous les éléments pour comprendre l’équation :
- Egalité entre deux expressions algébriques,
- Une ou plusieurs inconnues à trouver,
- Une variable appelée « x »,
- Utile à la résolution de problèmes.
Qu’il s’agisse d’une équation du second degré (forme réduite), d’une équation à une inconnue, d’une équation différentielle ou d'une équation logarithmique, on devrait être à même de les résoudre (et de les factoriser) avec quelques exercices interactifs.
Besoin de cours de maths terminale s ?
Pourquoi les équations sont difficiles ?
Prenons la question autrement : pourquoi les équations sont souvent perçues comme difficiles ?

Toute règle mathématique répond d'un raisonnement logique à acquérir. On commencerait à répondre en disant qu'en maths, rien n'est difficile : il suffit de comprendre la logique permettant de résoudre une équation algébrique, pour trouver une ou plusieurs variables inconnues.
« Les mathématiques sont une gymnastique de l'esprit et une préparation à la philosophie. »
Isocrate
Mais cette logique n'est pas intuitive pour tout le monde, et plusieurs défis récurrents peuvent se présenter aux élèves :
- Abstractions : difficulté à comprendre un concept théorique (par exemple, la notion d’infini ou d’équation sans solution) qui n’a pas toujours de traduction concrète.
- Étapes multiples : perdre le fil dans un raisonnement long, oublier une transformation ou sauter une ligne de calcul importante.
- Erreurs de calcul : confusion dans les signes (+/−), mauvaise gestion des fractions, oubli de parenthèses ou ordre des priorités mal respecté.
Les équations sont souvent perçues comme difficiles par les élèves parce qu'elles impliquent de jongler avec des variables inconnues. En somme, celles-ci sont difficiles, généralement parce que l'on cherche à déterminer l'existence ou l'absence de solutions et leur nombre éventuel s'il y en a.
Plus largement, il s'agit d'un univers très particulier, qui possède bien des secrets. On vous donne donc quelques conseils concrets pour la résolution d'équations, que ce soit de la mise en équation aux équations complexes.
Les compétences requises pour résoudre des équations
Réussir à résoudre une équation fait partie des bases pour apprendre les maths. L'objectif des programmes scolaires au lycée est de faire acquérir durant la scolarité des élèves, "l'esprit cartésien du mathématicien", ou tout simplement "l'esprit mathématique".
Pourquoi donc pas s'entraîner en cours de maths en ligne ou des cours de maths 3ème en méthodes de résolution ?
L’appréhension ressentie par de nombreux élèves quant à la discipline est liée en partie au fait qu’ils sont nombreux à ne pas voir l’utilité des maths dans la vraie vie. Pourtant, les maths induisent en effet un raisonnement logique : en vulgarisant, on dirait "c'est bon ou ça ne l'est pas".
En réalité, les maths font partie intégrante de nos vies quotidiennes, même si nous ne nous en rendons pas forcément compte : de la cuisine à l’achat d’une maison, en passant par le moment où l’on fait ses courses ou quand l'on calcule un budget prévisionnel pour les vacances par exemple, la matière est omniprésente dans nos vies.
- Comment, par exemple, calculer la pente du toit d'une maison que l'on rénove ?
- Quelle est la part du loyer et des factures dans le revenu mensuel net ?
- Comment amortir un véhicule nouvellement acheté ?
Le professeur de maths à l’école, au collège ou au lycée, ou encore le professeur particulier recruté sur Superprof, apporteront des compétences qui seront utiles tous les jours.
Propres à l’esprit mathématicien, elles sont en outre indispensables lorsque l’on veut résoudre une équation sans faire d’erreurs.
Ce qu'on appelle "l'esprit mathématicien" repose sur un socle de certaines dispositions qu'il faut entretenir.
La rigueur
Il est nécessaire d’être rigoureux quand on veut faire des maths.
Et cela plus particulièrement lorsque l’on chercher à résoudre des équations.
Lorsque l'on se trouvera face à des exercices de maths, ou bien en face d'un contrôle de connaissances, il faudra être précis et raisonner avec logique.
La mémoire
Les mathématiques font travailler la mémoire.
En s'entraînant régulièrement, l'on sera capable de faire le lien avec les leçons de maths et de les mettre en application pour résoudre l’équation proposée.
Aussi pourra-t-on se remémorer d’anciennes équations résolues qui sont ressemblantes en tous points.
A force de faire des exercices de maths, le cerveau va créer des connexions neurologiques et des automatismes vont se développer conjointement.
C'est la raison pour laquelle certains sont capables d'exécuter des calculs mentaux rapidement.
C'est parce qu'à un moment donné de leur vie, ils ont eu le déclic cognitif leur permettant d'analyser les termes et les valeurs mathématiques.
L’organisation
Faire une équation nécessite de procéder par étapes.

Il faut en effet d'abord séparer les termes, les regrouper par classes de valeurs (les variables connues du même côté, et d'un autre, les variables inconnues).
Il faut pouvoir simplifier l'opération.
Exemple :
L'équation 2x² + 6x + 4 + 4x² - 4x = 6x² - 12 + 4x donnera : 6x² + 2x + 4 = 6x² + 4x -12
On va chercher à regrouper les variables du même genre entre elles, donc d'abord additionner ou soustraire tous les x² ensemble, et ensuite les x et puis les nombres entiers.
Il faut faire attention aux changements de signes : lorsque l'on passe une valeur de l'autre côté de l'équation (du signe =), le signe s'inverse.
On obtient : 0x²-2x=-16.
D'où x= -16/-2, soit x=8.
Prenez toujours soin de vérifier le résultat en remplaçant la valeur de x trouvée dans tous les termes de l'équation.
(2x²+6x+4+4x²-4x)=404 et (6x²-12+4x)=404 pour x=8.
L’organisation, tant dans l'exercice que dans l'environnement de travail, permettra d’appréhender l’équation avec une certaine sérénité.
Il faudra aussi éviter à tout prix de trop s'éparpiller. Voici un exemple d'organisation pour résoudre une équation :
La persévérance
On admet aisément que devant un problème mathématique ou une équation, abandonner ne fournit aucune solution.
Tous les exercices de cette matière impliquent de persévérer lorsque l'on bloque au pied du mur.
Pour faire du super travail, il faut trouver un moyen soit de contourner le mur, soit de le franchir par un raisonnement logique.
C'est la raison pour laquelle en maths, on remplace souvent les x et les y par des nombres entiers et on regroupe les termes du même genre (les x² ensemble, les x ensemble et les entiers ensemble), afin de simplifier le calcul.
La logique
Bien qu’en répétant systématiquement les mêmes procédés de résolution d’équation, il est important de comprendre la logique sous-jacente à la résolution de ces problèmes.
En ce sens, la rigueur, l’organisation, l’entrainement et la mémoire permettent à terme de mieux cerner le processus et de résoudre ensuite en étant plus fluide dans son raisonnement.
Vous cherchez des cours de maths en ligne ?
Méthodes générales de résolution d'une équation
La méthode de la balance : idéale pour les débutants
Cette méthode repose sur l’idée que l’équation est comparable à une balance à deux plateaux. Les deux côtés doivent rester parfaitement équilibrés. Chaque opération réalisée d’un côté doit donc être reproduite exactement de l’autre pour conserver l’égalité.
Par exemple :
- Si on ajoute 3 à gauche, on doit aussi ajouter 3 à droite
- Si on divise un côté par 2, on divise l’autre côté par 2
Cette approche visuelle est très utile pour les débutants, car elle rend la logique de l’équation plus concrète. L’objectif est de simplifier progressivement jusqu’à isoler l’inconnue, tout en préservant l’équilibre de départ.
La méthode des opérations inverses : parfaites pour les intermédiaires
Cette méthode consiste à appliquer, dans l’ordre inverse, les opérations qui ont été effectuées sur l’inconnue pour l’isoler. On « défait » chaque transformation en utilisant son opération opposée.
Par exemple :
- Si l’inconnue a été multipliée par 4 puis augmentée de 5, il faut d’abord enlever 5, puis diviser par 4
- On part ainsi de l’extérieur vers l’intérieur de l’équation, un peu comme si on déroulait un fil
Cette approche aide à comprendre qu’une équation est une suite d’étapes logiques réversibles. Elle est très efficace pour des équations linéaires simples, mais peut aussi s’étendre à des cas plus complexes, dès lors qu’on identifie correctement les opérations dans l’ordre où elles ont été appliquées.
La méthode du recouvrement (terme caché) : pour les plus aguerris
Cette méthode, parfois appelée méthode du masquage ou du « cache », sert surtout aux débutants pour simplifier visuellement une équation complexe. L’idée est de remplacer temporairement une partie de l’équation compliquée (par exemple, une expression entre parenthèses ou un binôme) par une lettre ou un symbole simple.
Cela permet de transformer l’équation en une forme plus accessible
Une fois la résolution faite, on « enlève le cache » et on remplace par l’expression initiale pour poursuivre. Par exemple :
- Si on a (2x + 3)² = 25, on pose A = (2x + 3)
- Ce qui donne A² = 25, plus facile à résoudre
- Après avoir trouvé A, on revient à l’équation de départ pour déterminer x
Cette méthode aide à décomposer les difficultés et à gérer des équations imbriquées.

Méthodes de résolution par type d'équation mathématique

Résoudre une équation du premier degré
Les équations du premier degré apparaissent comme les équations les plus simples à résoudre.
En effet, trouver la solution pour une équation du premier degré n’implique que quatre type de calculs : l’addition, la soustraction, la multiplication et la division.
Si l'on doit résoudre une équation du premier degré à une inconnue, l'objectif est simple : il faut juste trouver et isoler la valeur de x (la fameuse inconnue).
Trouvez ici tous nos cours de maths terminale s.
Pour une équation simple, l'on va alors dans ce cas procéder par étapes :
- Isoler l’inconnue,
- Regrouper les termes,
- Diviser,
- Conclure par la solution, généralement nommée S.
Comme nous l’avons déjà expliqué, pour l’équation (3x-5 = –x +2), le calcul devra être similaire à celui-ci :
- 3x + x = 5 + 2 (ici, l’inconnue a été isolée),
- 4x = 7 (les termes ont été regroupés),
- x = 7/4 (division par 4).
Donc x = 7/4.
Au début - et pour montrer le raisonnement logique à l'examinateur ou au professeur -, ne pas hésiter à écrire toutes les lignes de la démonstration, même si celles-ci paraissent évidentes et simples comme bonjour.

Si une erreur de calcul s'immisce dans l'écriture du résultat, l'élève gardera quelques points au lieu d'avoir zéro s'il dévoile son raisonnement logique.
Les plus joueurs pourront désormais tenter de résoudre la plus célèbre des équations du premier degré de l’histoire des mathématiques : l’épitaphe (sur la tombe) du mathématicien Diophante d’Alexandrie.
Elle date du 3ème siècle de notre ère, et permet de trouver l'âge auquel il décéda.
Voici l'épitaphe présente sur sa tombe :
« Passant, sous ce tombeau repose Diophante.
Ces quelques vers tracés par une main savante,
Vont te faire connaître à quel âge il est mort.
Des jours assez nombreux que lui compta le sort,
Le sixième marqua le temps de son enfance ;
Le douzième fut pris par son adolescence.
Des sept parts de sa vie, une encore s'écoula,
Puis s'étant marié, sa femme lui donna,
Cinq ans après un fils qui, du destin sévère,
Reçut de jours hélas, deux fois moins que son père.
De quatre ans, dans les pleurs, celui-ci survécut.
Dis, tu sais compter, à quel âge il mourut. »
Transposée en termes mathématiques, voici l'équation à résoudre : x = x/6 + x/12 + x/7 + 5 + x/2 + 4.
Cela donne :
- x=2x/12+x/12+x/7+x/2+9,
- x=14x/84+7x/84+12x/84+42x/84+9 (tous les termes sont mis au même dénominateur),
- 84x/84 = 14x/84+7x/84+12x/84+42x/84+9,
- 84x/84 - (14x/84+7x/84+12x/84+42x/84) = 9,
- (84x/84)-(75x/84)=9,
- 9x/84=9,
- 9x=9x84,
- 9x=756,
- x=84.
Une équation de premier degré à une inconnue
Une équation est dite du premier degré si elle peut prendre la forme ax + b = 0 où a et b sont des nombres réels donnés, a étant non nul.
Diophante d'Alexandrie serait donc mort à l'âge de 84 ans.
Vous cherchez des cours de maths 3ème ?
Trouver la solution pour une équation à produit-nul
Une équation-produit est une équation du second degré.
@wonderwomath Quelles sont les solutions de l’équation (5x - 6)(4 - 2x) = 0 ? #prof #maths #equation ♬ CRAFT - OFEKNIV
Concrètement, une équation produit prend la forme suivante : (ax + b)(cx+d) = 0.
x est toujours l’inconnue, a, b, c, et d sont des valeurs fixes données dans l'énoncé de l’exercice.
Pour ceux qui sont plus à l’aise avec les chiffres qu’avec les inconnues, cela pourrait par exemple être 2x + 2.
Lors d'un prochain cours de maths sur ce type d’équations, l'enseignant expliquera certainement une règle élémentaire et fondamentale pour leur résolution : un produit de facteurs est nul si et seulement si au moins un des facteurs est nul.
Il faudra donc résoudre autant d’équations qu’il y a de facteurs !
On ne le répétera jamais assez : la meilleure façon d’apprendre est de s’entraîner et de faire des exercices corrigés par un professeur.
Voici donc un exemple d’équation produit-nul, avec sa solution de manière à ce que l'un des deux facteurs soit nul :
(2x + 4) × (2x – 6) = 0
Les deux facteurs correspondent aux deux groupes d’équation entre parenthèses. Il va donc falloir résoudre les deux.
Les solutions de l'équation (2x + 4)(2x – 6) = 0 sont les nombres x tels que :
- 2x + 4 = 0,
- 2x = -4,
- x = -4/2 = -2.
OU
- 2x - 6 = 0,
- 2x = 6,
- x= 6/2,
- x= 3.
Les solutions de l'équation (2x + 4)(2x - 6) = 0 sont -2 et 3.
Trouvez votre cours de maths seconde.
Résoudre une équation du second degré
Pour résoudre une équation du second degré, il faut être capable de maîtriser les équations du premier degré ainsi que les principes de résolution des équations produits.
Une équation de second degré
On définit une équation du second degré sous la forme ax² + bx + c = 0, avec a différent de 0.
Première chose, pour la résolution d’équation du second degré, il est important de connaître ses identités remarquables.
On rassure tout le monde, il n'y en a seulement 3 à connaître par cœur :
- a² + 2ab + b² = (a+b)²,
- a² - 2ab + b² = (a-b)²,
- a² - b² = (a+b)(a-b).
ATTENTION
(a+b)² n'est donc généralement pas égal à : a²+b² ! Il faut développer les termes pour trouver la bonne solution.
Reconnaître les identités remarquables permettra une résolution rapide de l’équation en question. En effet, elle permet de simplifier l'écriture d'une équation comme ceci :
@wonderwomath Peux-tu développer : (4-5a)² ? #prof #maths #lycee ♬ Love You So - The King Khan & BBQ Show
C’est la première étape de la résolution, chercher une forme particulière à l’équation.
Dans quelle mesure peut-elle s’écrire comme une expression d’une identité remarquable ?
Lorsque ce n’est malheureusement pas le cas, pas de panique, une autre solution existe mais elle nécessite l’apprentissage de quelques formules (3 au total, cela reste raisonnable).
Pour résoudre une équation de la forme ax² + bx + c = 0, il faut au préalable calculer le discriminant du trinôme, aussi appelé par la lettre grecque delta (Δ).
Celui-ci s’obtient par la formule suivante : Δ = b² - 4 ac.
Des lors, apparaissent trois cas de figures :
Lorsque Δ est négatif, la résolution est aisée puisqu’il n’existe pas de solution,
Lorsque Δ est égal à 0, il n’existe qu’une seule et unique solution qui est de la forme x = - b / 2a,
Enfin, lorsque Δ est positif, il existe deux solutions distinctes qui sont : X1 = (-b-√Δ)/(2a) ou X2 = (-b+√Δ)/(2a).
Un exemple pour mieux comprendre :
Pour résoudre l’équation 2x² + 5 x + 2, si on calcule le discriminant Δ, on obtient :
- Δ = b² - 4 ac,
- Δ = 5² - 4 * (2 * 2),
- Δ = 25 – 16 = 9 > 0 donc il existe deux solutions distinctes :
- x1 = -5 -√9 / (2*2) = -8/4 = -2,
- x2 = -5+√9 / (2*2) = -2/4 = -1/2.
Attention donc aux changements de signe dans le calcul du discriminant.
Il ne faut pas non plus se laisser décontenancer si on voit apparaître un x élevé au cube.
En effet, une équation de la forme x³ + 2 x² + 8 x peut se résoudre comme une équation du second degré, si on utilise la factorisation et que l’on factorise chacun des membres de l’expression par x.
Ainsi, l’équation devient x ( x² + 2 x + 8).
x = 0 est une solution de l’équation et en calculant le discriminant de x² + 2 x + 8, on trouvera une, plusieurs ou aucune autre solution à l’équation.
Besoin de cours de maths seconde ?
Le cas des équations-quotients
Une équation-quotient a pour règle un théorème :
Un quotient est nul si et seulement si son numérateur est nul et son dénominateur non nul.
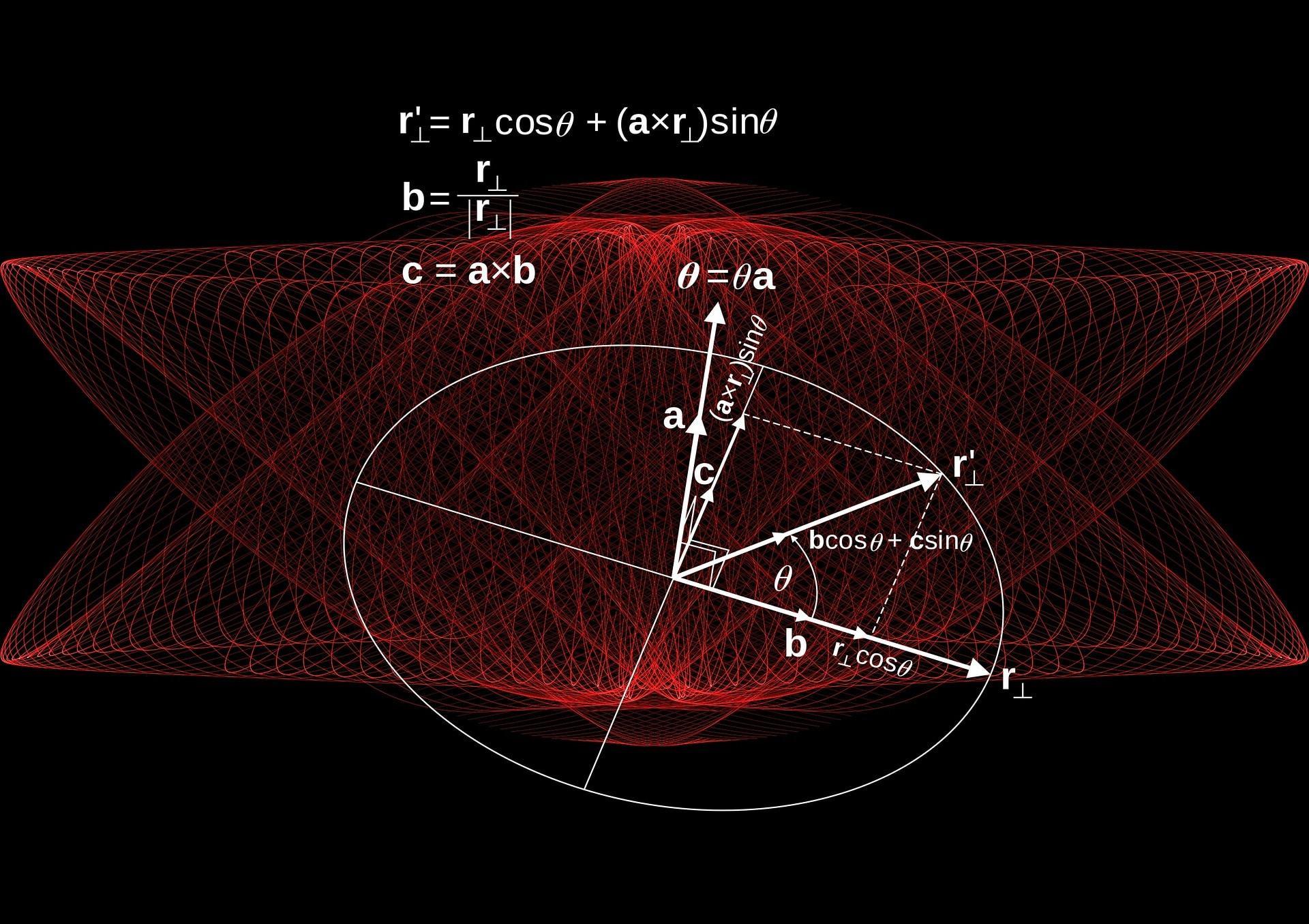
On sait que l'on a affaire à une équation-quotient si l'énoncé de l'exercice prend la forme suivante : f(x) / g(x) = 0.
Pour résoudre une équation-quotient, il faut :
- Exclure les valeurs interdites, c’est-à-dire celles qui annulent le dénominateur,
- Tout réduire au même dénominateur,
- Ramener à un quotient-nul,
- Résoudre l’équation,
- Vérifier que les valeurs obtenues ne sont pas des valeurs interdites.
Voici un exemple de résolution d’équation-quotient utilisant les produits en croix : x / x+1 = x-1 / x+2 :
- x (x + 2) = (x − 1),
- (x + 1) (x + 2) − (x − 1) (x + 1) = 0,
- x² + 2x – (x² – 1) = 0,
- x² + 2x – x² + 1 = 0,
- 2x + 1 = 0,
- x = -(1/2).
Il ne s’agit pas d’une valeur interdite.
Ainsi, la solution S = -(1/2).
Comment résoudre une équation à deux inconnues ?
Ici, le système de résolution change.
Il ne s’agit plus de déterminer la valeur d’une inconnue, il va falloir dans un premier temps exprimer une inconnue par rapport à l’autre (méthode par substitution), ou encore chercher à déterminer x pour ensuite déterminer y (méthode par combinaison).
En d’autres termes, avec deux inconnues x et y, on cherche combien de x valent un y ou vice-versa. C’est précisément ce que l’on fait lorsque l’on exprime x en fonction de y ou y en fonction de x dans la méthode par substitution.
Nous allons chercher à détailler, exemples à l’appui, ces deux méthodes : par combinaison et par substitution.
Méthode par combinaison
Que ce soit par substitution ou par combinaison, il est nécessaire d’avoir un système de deux équations pour déterminer la valeur de deux inconnues.
En effet, si l'on prend un cas très simple ou x + y = 1, il est impossible avec juste cette information de déterminer la valeur de x et de y. C’est pourquoi deux équations sont nécessaires.
Un exemple pour mieux comprendre la résolution par substitution, avec le système suivant :
- {2 x + 4 y = 20,
- {7 x + 8 y = 52.
Dans un premier temps, il va falloir « harmoniser » les équations, de sorte à avoir dans l’une comme dans l’autre soit le même nombre de x, soit le même nombre de y.
Dans cet exemple précis, il est possible de multiplier chacun des termes de la première équation par 3,5 pour obtenir le même nombre de x dans la première et dans la deuxième équation (en l’occurrence 7 x).
Néanmoins, il semble plus aisé ici de procéder avec les y, en multipliant chacun des membres de la première équation par 2.
Le choix entre l'un ou l'autre est arbitraire, il dépend de ce que l'on préfère faire.

On obtient pour la première équation : 2 ( 2 x + 4 y ) = 20 * 2 et donc le nouveau système suivant :
- {4 x + 8 y = 40,
- {7 x + 8 y = 52.
Maintenant que l’on a le même nombre de y dans la première et dans la deuxième équation (il aurait également été possible de procéder de la même façon avec x), l'on va effectuer une soustraction entre les deux équations.
On soustrait donc soit la première à la seconde, soit l’inverse, le résultat restera le même.
On a donc :
- (7 x + 8 y) – (4 x + 8 y) = 52 – 40,
- 7 x + 8 y – 4 x – 8 y = 12,
- 3 x = 12,
- D’ou x = 4.
Maintenant que l’on connaît la valeur de x, on remplace dans les équations de départ x par la valeur 4.
Le système de résolution de ce problème de math est alors le même qu’une équation du premier degré avec une seule inconnue.
On obtient pour la première équation :
- 2 * 4 + 4 y = 20,
- 4 y = 20 – 8,
- y = 12 /4 = 3.
On peut utiliser la seconde équation pour vérifier le résultat :
- 7 * 4 + 8 y = 52,
- 8 y = 52 – 28,
- y = 24 / 8 = 3.
Les solutions de l’équation sont donc x = 3 et y = 4 que l’on note : S = {4 ; 3}
Méthode par substitution

La méthode par substitution est légèrement différente.
Il s’agit d’exprimer directement x en fonction de y ou l’inverse.
Reprenons l’exemple précédemment utilisé :
- {2 x + 4 y = 20,
- {7 x + 8 y = 52.
Dans la première équation, on peut chercher à exprimer x en fonction de y.
- 2 x + 4 y = 20,
- 2 x = 20 – 4 y,
- x = 10 – 2 y.
Maintenant que l’on a une valeur de x en fonction de y, on va réintroduire cette valeur dans la seconde équation.
- 7 x + 8 y = 52,
- 7 ( 10 – 2 y) + 8 y = 52,
- 70 – 14 y + 8 y = 52,
- - 6 y = - 18 , d’ou y = 3.
On peut ensuite reprendre la première équation et à nouveau la résoudre comme une équation à une seule et unique inconnue.
- 2 x + 4 y = 20,
- 2 x + 4 (3) = 20,
- 2 x = 20 – 12,
- x = 4.
On constate que l’on obtient bien les mêmes résultats avec les deux méthodes.
Remarque :
Notons que tous les systèmes du premier degré avec deux inconnues peuvent être résolus par combinaison ou par substitution.
Dans certains cas, l’une des deux méthodes sera plus rapide que l’autre, dans d’autres cas, ce sera l’inverse.
Certains élèves sont plus à l’aise que d'autres avec la méthode par combinaison, d’autres préféreront l’utilisation de la méthode par substitution.
Le plus important est de se sentir à l’aise avec la méthode que l’on utilise.
Aller plus loin : mises en équation et autres types

La mise en équation d’un problème
Il peut être demandé de mettre un problème donné en équation lors des leçons de mathématiques, pendant les contrôles ou pendant une épreuve d’examen.
La méthodologie est simple, et doit encore une fois être rigoureuse si l’on veut s’assurer de donner une réponse juste :
- Lire plusieurs fois l’énoncé pour bien le comprendre,
- Déterminer l’inconnue (ou les inconnues) qui correspond généralement au nombre demandé dans la question posée par le problème,
- Traduire et simplifier le texte en écritures mathématiques,
- Résoudre l’équation obtenue,
- Inclure les lignes intermédiaires, étapes montrant le raisonnement,
- Vérifier le résultat plusieurs fois,
- Rédiger la réponse à la question.
Dans certains cas, il peut s’agir d’un problème géométrique.
La procédure est la même, il faudra simplement faire un schéma supplémentaire au brouillon à l’aide des cours de géométrie pour pouvoir le résoudre.
Voici typiquement un exemple de problème qui peut être mis en équation :
Trois cousins, Jean, Yanis et Lucas ont à eux trois 60 ans. Quel est l’âge de chacun, sachant que Lucas a le triple de l’âge de Yanis et que Jean a dix ans de moins que Lucas ?
Dans ce problème à résoudre, les inconnues à trouver à l’aide de plusieurs équations correspondent aux âges respectifs des trois cousins !
Comment résoudre une inéquation de premier degré ?
Au programme de la révision bac ou pour tous ceux qui doivent apprendre les maths au collège, figurent aussi les inéquations. Là encore, il faudra être à l'aise avec la décomposition des termes et prendre gare aux changements de signes.

Les équations et les inéquations sont utiles notamment durant les études supérieures en sciences pour calculer des modèles en physique-chimie ou pour préparer le concours de l'Agrégation de mathématiques.
C'est pourquoi il est nécessaire de les apprendre dès le lycée, car elles seront incontournables pour réussir la nouvelle mouture du bac, issue de la réforme de 2019-2020.
Voyons comment résoudre une inéquation de premier degré :
Soit l'inéquation suivante 4 x + 5 ≤ x - 2.
Résoudre cette inéquation revient à se demander quel est l'ensemble des nombres (des valeurs de x) pour lesquels nous avons 4 x + 5 inférieur ou égal à x - 2.
On procédera de la même façon que pour la résolution d'une équation de premier degré :
- 4 x + 5 ≤ x - 2,
- ⇔ 4 x ≤ x - 7 (l'on fait passer la valeur 5 de l'autre côté de l'inéquation en changeant son signe),
- ⇔ 4 x - x ≤ x - 7 - x,
- ⇔ 3 x ≤ -7,
- ⇔ x ≤ -7/3.
Les solutions de l'inéquation sont donc l'ensemble des nombres inférieurs ou égaux à -7/3.
Autrement dit, l'ensemble des valeurs inférieures ou égales à l'inéquation 4 x + 5 ≤ x - 2 sont l'ensemble des nombres réels et décimaux définis sur une intervalle infinie jusqu'à la valeur -7/3 incluse.
Étudier d'autres types d'équations plus complexes
Chaque chapitre comporte son lot de réjouissances pour les révisions du bac : parmi ceux-ci, le calcul différentiel et les équations différentielles.
L'équation la plus difficile
L'équation la plus compliquée au monde est appelée « le dernier théorème de Fermat » et a été posé par le mathématicien français Pierre Fermat en 1637. Elle a été résolu par Andrew Wiles en 1994.
Résoudre des équations différentielles
Celles-ci est une équation où l’inconnue est une fonction, et qui se présente sous la forme d’une relation entre cette fonction et ses dérivées.
Il faut donc maîtriser l'étude de fonction et savoir dériver une équation.
Soit f(x) = y'=ay+b, où y est la fonction inconnue, a et b sont des nombres connus et f est une fonction connue.
Les solutions sur l'ensemble des nombres réels (l'annotation est R) de l'équation différentielle y'=ay+b, sont les fonctions f(x) = keax - b/a, où k est une constante réelle quelconque.
Bien entendu, les équations différentielles ne sont pas pour tous niveaux, c'est au programme de la Terminale scientifique.
Résoudre des équations logarithmiques
Ce type d'équation n'est pas ce qu'il y a de plus facile, mais les cours à domicile pourront peut-être éclairer tout apprenant dans l'impasse.
Commencez par transformer l'équation logarithmique par une équation avec des exposants.
y = logb (x) si et seulement si by = x.
La valeur de b doit être strictement positive, et ne doit pas être égale à 1.
Il va nous falloir identifier la base (b), la puissance (y) et l'expression exponentielle (x).
Soit l'équation 5 = log4(1024) :
- b = 4,
- y = 5,
- x = 1024.
Élevez ensuite la base à la puissance indiquée : 45 = 1024.
Pour trouver la valeur de x, il va maintenant falloir isoler le logarithme népérien.
Pour y parvenir, on fait passer tous les membres non logarithmiques de l'autre côté de l'équation :
- log3(x + 5) + 6 = 10,
- log3(x + 5) + 6 - 6 = 10 - 6,
- log3(x + 5) = 4.
L'écriture logarithmique doit être transposée en écriture exponentielle pour trouver x.
On obtient 34 = x + 5 (en suivant la formule y = logb (x) si et seulement si by = x).
Nous voilà maintenant face à une équation de premier degré, il devient aisé de trouver x :
- 34 = x + 5,
- x + 5 = 81,
- x = 76.
Nos conseils pour progresser en mathématiques
Plusieurs solutions s’offrent à quiconque souhaite se perfectionner en maths et approfondir durablement ses compétences en équations. Des cours particuliers maths avec un professeur à domicile vont faire progresser de façon significative.
Un professeur de maths a pour rôle d'épauler son apprenant, mathématicien apprenti, le guider vers des mécanismes de compréhension et des automatismes dans des sujets tels que la dérivée, les vecteurs, le nombre complexe ou les matrices.
profs de maths pour progresser !
Ne pas hésiter à solliciter l'un d'entre-eux dans votre ville pour progresser en mathématiques, pour s'entraîner avant ou pendant l'année scolaire.
Que l'élève ait des difficultés pour résoudre une équation, pour factoriser une expression, qu'il soit fâché avec les nombres décimaux, les nombres relatifs, les nombres rationnels ou les nombres réels...
Que l'on souhaite résoudre des énigmes mathématiques, un professeur de maths pédagogue sera là pour accompagner et trouver la méthode adéquate.
Il saura expliciter, transmettre les systèmes d’équations au rythme de son élève, et ce, avec une pédagogie ludique et interactive.
Réviser régulièrement en réalisant des fiches de révision ou encore suivre des cours de maths en ligne sur Youtube, en parallèle des cours particuliers maths, aideront aussi, à devenir meilleur en maths ! Et n'oubliez jamais que personne n'est nul en maths !
En synthèse :
- Les équations et inéquations sont au cœur de l’arithmétique (à ne pas confondre avec l’algèbre) et occupent une place de choix dans la discipline mathématique et dans de nombreux exercices mathématiques,
- Que ce soit pour les polynômes avec les équations polynomiales ou les équations diophantiennes, en trigonométrie avec les équations trigonométriques, équations du premier ou du deuxième degré, à une ou plusieurs inconnues, il y a fort à parier pour qu’elles suivent l'élève tout au long de sa scolarité et éventuellement de son parcours universitaire pour les plus matheux,
- Les maths - calcul d'aire, représentation graphique, étude de fonction exponentielle, l'algèbre linéaire ou les probabilités (loi normale, loi binomiale, loi de Bernoulli), peuvent servir toute la vie et aident à avoir un raisonnement cognitif plus rapide ainsi qu'un réflexion cartésienne et / ou rationnelle.
Sources
- Educsol,
« Résolution d’équations du premier degré à une inconnue
», 2024, https://eduscol.education.fr/document/59725/download. Consulté le 1er Septembre 2025. - L'Etudiant, « Résoudre des équations à deux inconnues », 8 Décembre 2022,https://www.letudiant.fr/college/methodologie-college/article/comment-resoudre-des-equations-lineaires-a-deux-inconnues.html. Consulté le 1er Septembre 2025.
Résumer via IA :















J’ai aimé ! Merci beaucoup
Ouais
j’adore ! meciiii
Merci beaucoup! Grâce à toi, je comprends les mathèmatiques. :)
Merci beaucoup pour le cours :)
Ouais
Merci beaucoup! Vous avez fait un article très utile et intéressant. J’ai l’aimé. Vous avez expliqué les terms nécessaires pour comprendre et vous avez utilisé des exemples avec les résultats.
J’ai besoin d’aide svp avec mes devoirs d’equoition données moi cette réponse svp
Merci beaucoup pour cet article il est très utile
Pourquoi il est question que de première ES ou S, il n’y a pas que ces deux filières qui proposent des cours de maths assez poussés. Encore que ES, sa me parait bizarre.
bonjour jai des exercice sur le programme de calcule povez vous m aidez sil vous plais
Bonjour j’ai un exercice et j’ai vraiment besoins d’aide
Bonjour Mariane,
Pour vous aider à résoudre votre problème, nous vous invitons à demander de l’aide à vos camarades ou bien à un professeur particulier. Vous avez également des applications qui permettent d’entrer en contact avec des professeurs afin de résoudre un problème.
Bien à vous
Slu mais moi j’ai des problemes pour resoudre les longues equations
Merci beaucoup , c’est parfait
(3×2)+6÷2
(3×2)+6÷2
=6+3
=9
Resoudre l equoition 4_(x_2)=5x_(2x_7)
Résoudre l’équation 11z-9,7=10-(-4,6+5z)
J’ai un exercice à faire avec des équations de seconds degrés
Bonjour, quel est le nombre ×-3,5 et qui est égal à 8 merci beaucoup
Cool, comme ça les prêtres apprennent les maths tranquillement. Pour ta question je crois que c’est 4,5 la réponse
Cet article m’est très utile
Merci :)
Très interessant
2x – 6x+12=0
-4x = -12
X=3
3
Voici mon problème (2×9-6)/3=
Je cherche la réponse et je crois que le chiffre est 4
Jolie mais quel jolie
J’ai besoin d’aide svp avec mes devoirs d’equoition données moi cette réponse svp
200x + 125y =40 ?
S’il vous plaît aide moi. Définie par :P(x)=2x²-x-6 1.résous l’équation P(x)=0. 2.déduis-en la factorisations de P(x). 3.etudie le signe de P(x). 4.déduis-en les solutions de l’inéquation P(x)≤0
Bonsoir. A partir d’un certain âge, on n’accepte plus ce que l’on ne comprend pas… Comment faire ?
Bonjour,
Il faut travailler sur sa patience, prendre le temps d’essayer de comprendre en utilisant les corrigés.
Bon courage
hi i’m samar
Merci de m’avoir aide