"La mathématique universelle est une logique de l'imagination."
Gottfried Wilhelm Leibniz (1646-1716)
En cours de math au collège, les élèves découvrent les bases des statistiques et de la géométrie, notamment le calcul de la moyenne et de la médiane. Souvent incomprise, la médiane est un indicateur central de l'analyse des probabilités, des démonstrations de géométrie et de l'analyse statistique.
À ne pas confondre avec la moyenne, la médiane est la valeur qui se situe au centre d'une suite de données lorsque ces données sont ordonnées (par ordre croissant ou décroissant par exemple). Alors que la moyenne se calcule en divisant la somme des données par le nombre de données, la médiane, elle, se trouve en cherchant la valeur centrale :
- Si l’effectif total est impair, la médiane est la valeur centrale de la série,
- Si le groupe contient une valeur paire, la médiane est alors la moyenne des deux valeurs centrales de la série.
Nul besoin alors de réaliser la somme des données comme c'est le cas afin de trouver la moyenne. Superprof se met dans la peau d'un professeur de maths pour vous expliquer comment trouver et interpréter une médiane ! Tous à vos crayons !

Qu'est-ce que la médiane en mathématiques ?
Pour bien comprendre, et avant de se lancer dans des longues lignes de calculs et de formules, il faut bien comprendre de quoi l'on parle.
En cours de math en ligne, la médiane, concrètement, désigne une valeur permettant de séparer un groupe de données en deux parties égales. Le calcul de la médiane d'une série est très utilisé en statistiques, car il permet une analyse beaucoup plus affinée que celle de la moyenne.
La médiane représente la valeur centrale d'une série statistique.
Pour identifier cette valeur, il s'agit de ranger l'ensemble des données de la plus petite valeur à la plus grande. Sitôt cette liste ordonnée en ordre croissant obtenue, vous pourrez facilement trouver la valeur qui partage la population étudiée en deux sous-ensembles de mêmes effectifs.
👉 Prenons l'exemple d'un coach de natation qui souhaiterait former deux groupes d'élèves aux niveaux de natation différents. Supposons qu'il demande à 9 nageurs apprentis d'effectuer deux longueurs en nage libre, puis relève ensuite les temps de parcours réalisés :
- 30,6 ; 29,1 ; 32,9 ; 35,1 ; 30,0 ; 36,4 ; 31,7 ; 35,5 ; 33,9
La liste ordonnée de cette série de valeurs est : 29,1 ; 30,0 ; 30,6 ; 31,7 ; 32,9 ; 33,9 ; 35,1 ; 35,5 ; 36,4.
Elle permet, d'une part, de classer les performances en deux catégories de même nombre : d'un côté, les quatre nageurs les moins bons et de l'autre, les quatre meilleurs nageurs.
Que se passe-t-il si un autre élève rejoint le cours ?
Supposons qu'un 10ème nageur effectue ses traversées en 28,7 secondes. De ce fait, le nombre d'observations augmente, et l'effectif de la classe devient pair (avec 10 valeurs). Le "milieu" de la population comporte alors deux valeurs : 31,7 et 32,9. Pour faire le calcul de la médiane avec deux nombres au milieu de l'échantillon, on va calculer la moyenne des deux valeurs centrales :
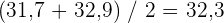
Conclusion :
- Si l’effectif total est impair, la médiane est la valeur centrale de la série,
- Si le groupe contient une valeur paire, la médiane est alors la moyenne des deux valeurs centrales de la série.
Autrement dit :
- ((N+1)/2) ème valeur pour un nombre de données impair,
- La moyenne des (N/2)ème et (N+1)/2ème valeurs pour un nombre de données pair.
Plutôt simple, non ? Découvrez comment faire un cône en papier !
Trouver la médiane dans une série statistique discrète
En statistiques, une variable est discrète lorsqu'elle contient un nombre défini de valeurs réelles.

Par exemple, les notes obtenues par les élèves d'une classe de seconde lors d'un contrôle de mathématiques sur les statistiques descriptives. Supposons que la distribution des notes soit 5, 12, 11, 10, 6, 17, 11, 12, 10, 13, 9, 11, 12, 8, 7, 10, 11, 10, 12, 11, 9, 10, 8, 11.
Ordonner les valeurs dans un tableau statistique
En cours de maths, la méthodologie pour trouver la valeur médiane consiste en un premier temps à ordonner la série dans un tableau en notant les valeurs par ordre croissant, et les effectifs (le nombre d'élèves ayant obtenue telle ou telle note) dans une seconde ligne.
On obtient un tableau tel que :
| Xi | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 17 |
|---|---|---|---|---|---|---|---|---|---|---|
| Ni | 1 | 1 | 1 | 2 | 2 | 5 | 6 | 4 | 1 | 1 |
- Xi : 5, 6, 7, 8, 9, 10, 11, 12, 13, 17, est la série ordonnée de notes,
- Ni : 1, 1, 1, 2, 2, 5, 6, 4, 1, 1, est ici le nombre d'élèves ayant obtenu la note susmentionnée,
- Effectifs cumulés croissants : 1, 2, 3, 5, 7, 12, 18, 22, 23, 24 est donc la somme des Ni + la valeur inférieure.
Cinq élèves ont eu 10, un élève a eu 17, quatre élèves ont eu 12, etc. En additionnant les effectifs (Ni) des valeurs inférieures, on obtient ce qu'on appelle les effectifs cumulés croissants. Ils sont utiles pour connaître les effectifs d'une catégorie de valeurs. Par exemple, 12 élèves ont obtenu une note inférieure à 10.
Calculer les fréquences cumulées croissantes peut permettre, dans certains cas, de visualiser les résultats en pourcentages : c'est notamment utile pour représenter la proportion de chacun des effectifs par rapport à la population globale.
👉 Exemple : avec un salaire médian établit à 1 789 € nets en France en 2020, 50 % de la population active perçoit moins de 1 789 € par mois.
Déterminer la médiane
Si l'effectif est impair, la médiane est la (N+1)/2ème valeur. Ici, Ni est un nombre pair (24). La médiane, qui sépare le nombre d'individus en deux parties égales, est donc la moyenne des (N/2)ème et (N+1)/2ème valeurs. Soit, dans notre exemple, la moyenne entre la 12ème et la 13ème valeur : Me = 10,5. Comment factoriser en maths ?

Calculer la médiane d'une série statistique continue
Il arrive souvent que les valeurs prennent des nombres infinis ou un nombre de valeurs indénombrable.
On se trouve alors confronté à une infinité de valeurs comprises dans un intervalle. Par exemple, les températures. La température est une variable quantitative d'intervalle continue, car elle peut avoir une infinité de valeurs : entre 30 °C et 31 °C, on peut avoir 30,1 °C, 30,5 °C mais aussi 30,99999 °C ou 30,00001 °C, etc.
La première étape consiste à dresser la courbe des fréquences cumulées croissantes, pour identifier la médiane et les quartiles de la série. Par exemple, si l'on souhaite mesurer la proportion de personnes gagnant entre 500 € et 2 100 € par mois, supposons que l'on ait la distribution de revenus suivante :
- 40 personnes gagnent entre 500 et 800 € par mois,
- 31 ont entre 800 et 1 100 €,
- 25 ont entre 1 100 € et 1 200 €,
- 52 actifs perçoivent entre 1 200 € et 1 500 € par mois,
- 37 personnes ont entre 1 500 € et 1 800 €,
- 18 ont entre 1 800 € et 2 000 €,
- 27 personnes gagnent entre 2 000 € et 2 100 €.
L'effectif, N est de 230. On en déduit les fréquences et les fréquences cumulées croissantes. Ensuite, tracez la courbe des fréquences cumulées croissantes sur un repère orthonormé, avec en abscisses les valeurs et les fréquences cumulées croissantes sur l'axe des ordonnées. De cette manière, on peut faire une lecture graphique de la médiane, sans passer par les formules de calcul.
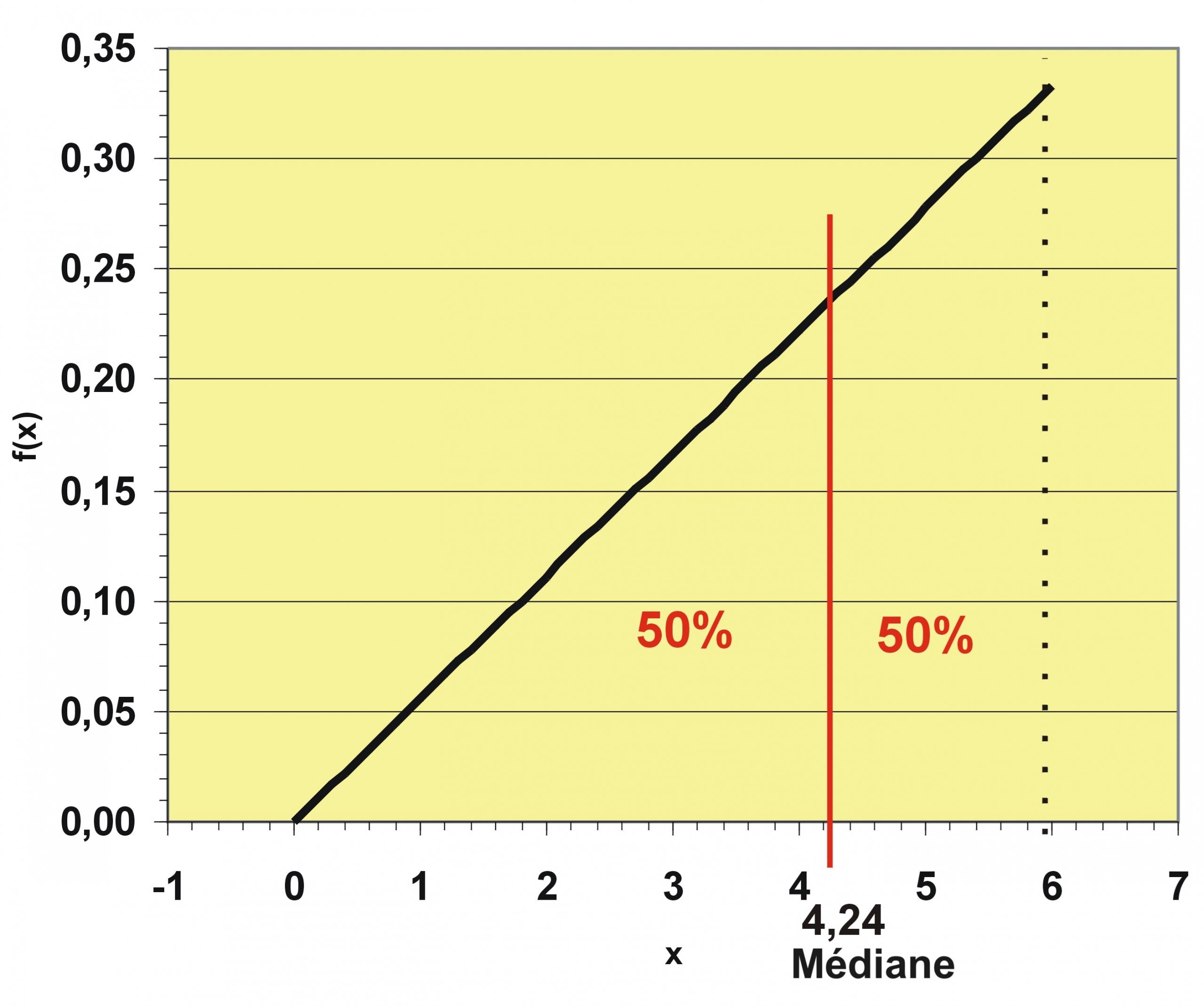
On lit donc que la médiane de notre échantillon est 13 (un salaire médian de 1 300 € dans notre exemple). Les quartiles, situés aux niveaux des 25 % et 75 % ont donc pour valeurs respectives 9,7 et 17.
Lecture : 25 % des valeurs de la série sont inférieures ou égales à 9,7. Et 75 % des valeurs sont inférieures ou égales à 17. On en déduit que 25 % des valeurs de la série sont comprises entre 17 et 21.
Dans notre exemple, l'interprétation de la médiane serait donc le suivant : 25 % des actifs de l'échantillon ont un revenu inférieur ou égal à 970 € par mois et 75 % des personnes perçoivent moins de 1 700 €. Par interpolation linéaire, on voit que 25 % de l'échantillon gagne entre 1 700 € et 2 100 € par mois.
Vous pouvez vous amuser, au passage, à calculer les déciles et les centiles afin de calculer la dispersion des revenus d'une classe de population donnée. Apprenez à faire un pavage en maths en prenant des cours de maths !
Le calcul de la médiane en géométrie
En géométrie, la médiane est également très utilisée, spécialement dans les représentations géométriques du triangle.

Figure de proue du programme de 4ème au collège, la médiane du triangle est pourtant parfois difficile à comprendre pour les adolescents.
Selon Fabienne Rosenwald, directrice de l'agence de statistiques du ministère de l'Education Nationale, le niveau en maths des élèves de 4ème en 2019 était équivalent à celui des élèves de 5ème en 1995. Ce chiffre édifiant n'est que le reflet du nombre de redoublements qui ont lieu chaque année en France. Prendre des cours de soutien scolaire en maths est alors parfois nécessaire pour la réussite scolaire de chaque élève.
Mais avant cela, découvrez la suite des explications !
La médiane d'un segment est la droite qui passe par son milieu et par le sommet opposé à ce segment.

Ainsi, dans un triangle ABC, la médiane issue du sommet A est la droite (AI), avec I comme milieu du segment [AB]. Partant, les segments [AI] et [IB] sont de même taille. Et l'aire du triangle ABI est égale à celle du triangle ACI.
Cela permet d'aborder un thème central de la géométrie : le théorème de la médiane.
Celui-ci stipule que si [BC] est séparé en son milieu par le point I, alors : 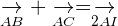
Autre règle : les trois médianes d'un triangle sont coucourantes. Leur point d'intersection, au centre de la figure, est l'isobarycentre des sommets : le centre de gravité du triangle.
Vous saurez que dans un triangle isocèle, la médiane est un axe de symétrie du triangle : si, dans un triangle, deux médianes sont de même longueur, alors le triangle est isocèle.
Dans un triangle rectangle en revanche, la médiane est issue du sommet opposé à l'angle droit du triangle : elle mesure la moitié de l'hypoténuse (oui oui, le célèbre segment à mettre au carré dans le théorème de Pythagore !). Si à l'inverse, dans un triangle, la longueur d'une médiane équivaut à la moitié de la longueur du côté correspondant, alors le triangle est rectangle. Apprenez le développement en mathématiques !
Ne pas confondre la moyenne avec la médiane
Attention à ne pas faire l'erreur, très répandue, de confondre médiane et moyenne.

Alors que les valeurs extrêmes d'une série ont une influence sur le calcul de la moyenne, celles-ci n'en ont aucune sur la médiane.
La moyenne arithmétique permet de résumer des valeurs numériques en un seul nombre réel et se calcule en prenant la somme des termes divisés par l'effectif total. À contrario, les grandeurs n'ont aucune incidence sur la médiane puisque cette valeur ne fait que mettre en lumière où se trouve le milieu d'une série ordonnée. De plus, c'est un indicateur idéal pour analyser une variable statistique, offrant des analyses bien plus fines que le simple calcul de la moyenne.
Pour résumer :
- Elle permet de trouver la valeur qui se situe au milieu d'une série de données.
- Elle se calcule en réalisant la moyenne des deux valeurs centrales (série paire) ou en trouvant celle se situant juste au centre (série impaire).
- Les valeurs extrêmes d'une série n'ont pas d'influence sur le calcul de la médiane.
- Elle permet de résumer des valeurs numériques en un seul nombre réel.
- Elle se calcule en prenant la somme des termes divisés par l'effectif total.
- Les valeurs extrêmes d'une série ont une influence sur le calcul de la moyenne.
Petit détour par l'économie pour comprendre :
👉 Par exemple, le salaire moyen en France était de 39 346 € bruts par an en 2019, soit 3 278 € par mois. Or les statistiques obtenues autour de la moyenne des salaires masquent de profondes inégalités de revenus. Les très hauts revenus (millionnaires et milliardaires) faisant mécaniquement augmenter la moyenne, alors que 50 % de la population active française vit actuellement avec moins de 20 000 € par an, soit 1 666 € mensuels. A 1 789 €, le salaire médian en France, est lui, beaucoup plus proche du revenu des 50 % des moins riches. C'est la raison pour laquelle il faut s'intéresser aux quartiles (25 % et 75 %) ainsi qu'à la médiane pour avoir une analyse statistique plus fine des valeurs prises.
Vous l'aurez compris, vous intéresser aux mathématiques et aux statistiques descriptives vous permettra de solutionner de nombreuses problématiques dans votre quotidien ! Alors, vous la sentez apparaître la bosse des maths ?
Résumer via IA :
















Je ne comprends rien, explication insuffisante pour expliquer l’exemple !!!