Les maths peuvent être définies comme la science dans laquelle on ne sait jamais de quoi l'on parle, ni si ce que l'on dit est vrai.
Bertrand Russel
Un tableau de variation est un outil mathématique qui résume le comportement d'une fonction. Il montre, à l'aide de flèches, sur quels intervalles la fonction "monte" (elle est croissante) ou "descend" (elle est décroissante). Il permet aussi de repérer facilement ses points les plus hauts (maximum) et les plus bas (minimum).
En mathématiques, et surtout au lycée, l'étude de fonction est un passage obligé. Au cœur de cette analyse se trouve un outil puissant mais parfois redouté : le tableau de variation. À quoi sert-il ? Comment le construire sans se tromper ?
Pas de panique ! Cet article est conçu en deux parties :
- D'abord, un guide simple, étape par étape, pour que n'importe qui puisse comprendre et dresser un tableau de variation.
- Ensuite, une section plus détaillée pour ceux qui veulent approfondir, avec des exemples concrets et des astuces pour éviter les erreurs classiques.
Suivez le guide, les variations de fonctions n'auront bientôt plus de secret pour vous !

Partie 1 : La méthode simple pour dresser un tableau de variation en 4 étapes
Oubliez les formules complexes pour l'instant. Construire un tableau de variation suit une logique en 4 étapes claires. Nous allons les parcourir ensemble.
Etape 1 : calculer la dérivée de la fonction
La première étape, incontournable, est de calculer la fonction dérivée, notée f'(x). C'est la dérivée qui va nous donner le "sens de la pente" de notre courbe.
Pour une fonction simple (polynôme)
- La dérivée de
 est
est  .
.
- La dérivée de
 est
est 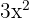 .
.
- La dérivée d'un nombre seul (une constante) est toujours
 .
.
- On dérive chaque terme de la fonction l'un après l'autre.
Pour la fonction 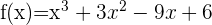 , sa dérivée est
, sa dérivée est 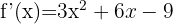 .
.
Pour une fonction produit ou quotient
- La règle du produit : si
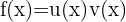 , alors
, alors 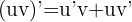 .
. - La règle du quotient : si
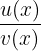 , avec
, avec 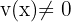 , alors
, alors 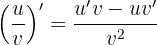 .
.
On dérive séparément u et v , puis on applique la formule en gardant l’ordre des termes. Pour le quotient, n’oubliez pas le carré du dénominateur.
Prenons 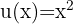 et
et 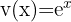 .
.
Alors 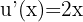 et
et 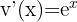 .
.
Pour le produit : 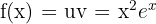 et la dérivée
et la dérivée 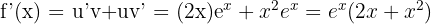 .
.
Pour le quotient : 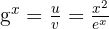 et la dérivée
et la dérivée 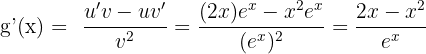 .
.
Pièges fréquents
Attention à ne pas oublier v2 au dénominateur dans le quotient et à ne pas inverser l’ordre u′v−uv′.
Etape 2 : étudier le signe de cette dérivée
C'est l'étape la plus importante ! Le signe de la dérivée  nous dit tout sur les variations de la fonction
nous dit tout sur les variations de la fonction  :
:
- Si
 est positive (+) sur un intervalle, alors la fonction
est positive (+) sur un intervalle, alors la fonction  est croissante (elle monte ↗) sur cet intervalle.
est croissante (elle monte ↗) sur cet intervalle. - Si
 est négative (-) sur un intervalle, alors la fonction
est négative (-) sur un intervalle, alors la fonction  est décroissante (elle descend ↘) sur cet intervalle.
est décroissante (elle descend ↘) sur cet intervalle.
Pour trouver le signe, on cherche d'abord les valeurs où la dérivée s'annule  . Ces valeurs sont les "points critiques" où la fonction peut changer de sens.
. Ces valeurs sont les "points critiques" où la fonction peut changer de sens.
- Exemple reformulé : Pour notre dérivée
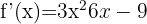 , on cherche quand elle est égale à zéro. On trouve que cela se produit pour
, on cherche quand elle est égale à zéro. On trouve que cela se produit pour  et
et  . On peut alors construire un tableau de signes pour
. On peut alors construire un tableau de signes pour  .
.

Etape 3 : identifier les points importants (extremums)
Les "points critiques" trouvés à l'étape 2 (où la dérivée s'annule) correspondent à des sommets ou des creux sur la courbe. On les appelle les extremums.
Calculez la valeur de la fonction  pour chacun de ces points.
pour chacun de ces points.
Pour notre fonction 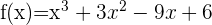 :
:
- pour
 , on calcule
, on calcule 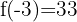 . Il s'agit du maximum local
. Il s'agit du maximum local - pour
 , on calcule
, on calcule 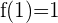 . Il s'agit du minimum local.
. Il s'agit du minimum local.
Etape 4 : dessiner le tableau de variation
Vous avez maintenant toutes les informations ! Il ne reste plus qu'à les assembler dans un tableau propre.
- Première ligne
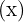 : Écrivez les bornes du domaine de définition (souvent
: Écrivez les bornes du domaine de définition (souvent  et
et 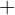 ) et les valeurs critiques trouvées à l'étape 2, dans l'ordre croissant.
) et les valeurs critiques trouvées à l'étape 2, dans l'ordre croissant. - Deuxième ligne (signe de
 ) : Indiquez le signe (+ ou -) de la dérivée sur chaque intervalle. Mettez un "0" sous les valeurs critiques.
) : Indiquez le signe (+ ou -) de la dérivée sur chaque intervalle. Mettez un "0" sous les valeurs critiques. - Troisième ligne (variation de
 ) : Dessinez les flèches. Une flèche qui monte (↗) si le signe est +, une flèche qui descend (↘) si le signe est -.
) : Dessinez les flèches. Une flèche qui monte (↗) si le signe est +, une flèche qui descend (↘) si le signe est -. - Complétez avec les valeurs : Au bout des flèches, écrivez les valeurs des extremums calculées à l'étape 3, ainsi que les limites de la fonction aux bornes (si demandées).
Et voilà ! Vous avez dressé votre tableau de variation.

Partie 2 pour les passionnés : analyse détaillée et exemples
Maintenant que la méthode est claire, plongeons dans les détails techniques pour maîtriser parfaitement l'étude de fonctions.
Qu'est-ce qu'un tableau de variation ?
Un tableau de variation est un outil de synthèse mathématique. Il résume sur deux ou trois lignes toutes les informations essentielles sur le comportement d'une fonction :
- La première ligne indique les valeurs clés de
xsur l'ensemble de définition. - La dernière ligne utilise des flèches pour représenter la monotonie de la fonction (si elle est croissante ou décroissante). Il permet de visualiser immédiatement où se situent les extremums (maximums et minimums locaux).
Pourquoi utiliser un tableau de variation ?
Le tableau de variation condense, en quelques lignes, tout ce qu’il faut savoir sur le “comportement” d’une fonction. Il évite les calculs répétitifs et prépare un tracé propre et argumenté.
1️⃣ Le tableau de variation permet de comprendre le comportement global sans tester des centaines de points :
- Le signe de la dérivée f′ permet de savoir où la fonction est croissante (f′ > 0) ou décroissante (f′ < 0) d’un seul coup d’œil.
- Les changements de signe de f′ indiquent immédiatement les zones de montée/descente et la structure globale (ex. “↗ puis ↘ puis ↗”), sans dresser un tableau de valeurs interminable.
- Les limites en −∞ et +∞, et aux éventuelles bornes ou asymptotes, placées en haut/bas du tableau, donnent le “cadre” du graphe (tend vers +∞, −∞, une valeur finie, etc.).

2️⃣ Le tableau de variation permet de trouver rapidement maxima et minima sur un intervalle :
- Aux points où f′ s’annule et change de signe :
- de + à − → maximum local,
- de − à + → minimum local.
- Sur un intervalle fermé [a; b], le tableau de variation permet de comparer en un clin d’œil f(a), f(b) et les valeurs en points critiques (où f′ = 0 ou f′ n’existe pas) pour déterminer les extrema globaux, sans passer par des essais/erreurs.
3️⃣ Le tableau de variation permet de préparer un tracé précis et propre de la courbe :
- En réunissant variations, valeurs clés (images de quelques abscisses utiles), limites et éventuelles asymptotes, on obtient un “plan de construction” fiable de la courbe.
- Les transitions (↗/↘) autour des extremums guident la forme locale (bosse/creux) et réduisent les risques d’erreur de croquis.
- Le tableau sert aussi de support d’explication: chaque élément du graphe est justifié (par un signe de dérivée, une limite, une valeur calculée).
Remplissez d’abord la ligne de f′ (signe, zéros, non-dérivabilité), puis déduisez la ligne de f (↗/↘). Ajoutez ensuite limites et valeurs remarquables.
Cela servira pour vos cours de maths, ainsi que pour mieux réviser avec les annales bac.
Des exemples pratiques de tableaux de variation
Voici quelques exemples supplémentaires pour aller plus loin.
Exemple 1 : la fonction quadratique
Prenons la fonction 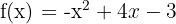 .
.
- Etape 1 : la dérivée est
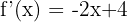 .
. - On résout
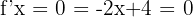 . Résultat :
. Résultat :  .
. - Sur l'intervalle −∞ et 2, f est positive donc elle est croissante et sur l'intervalle 2 et +∞, f est négative, donc elle est décroissante.
- Calculons maintenant l'extremum :
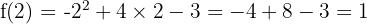 .
.
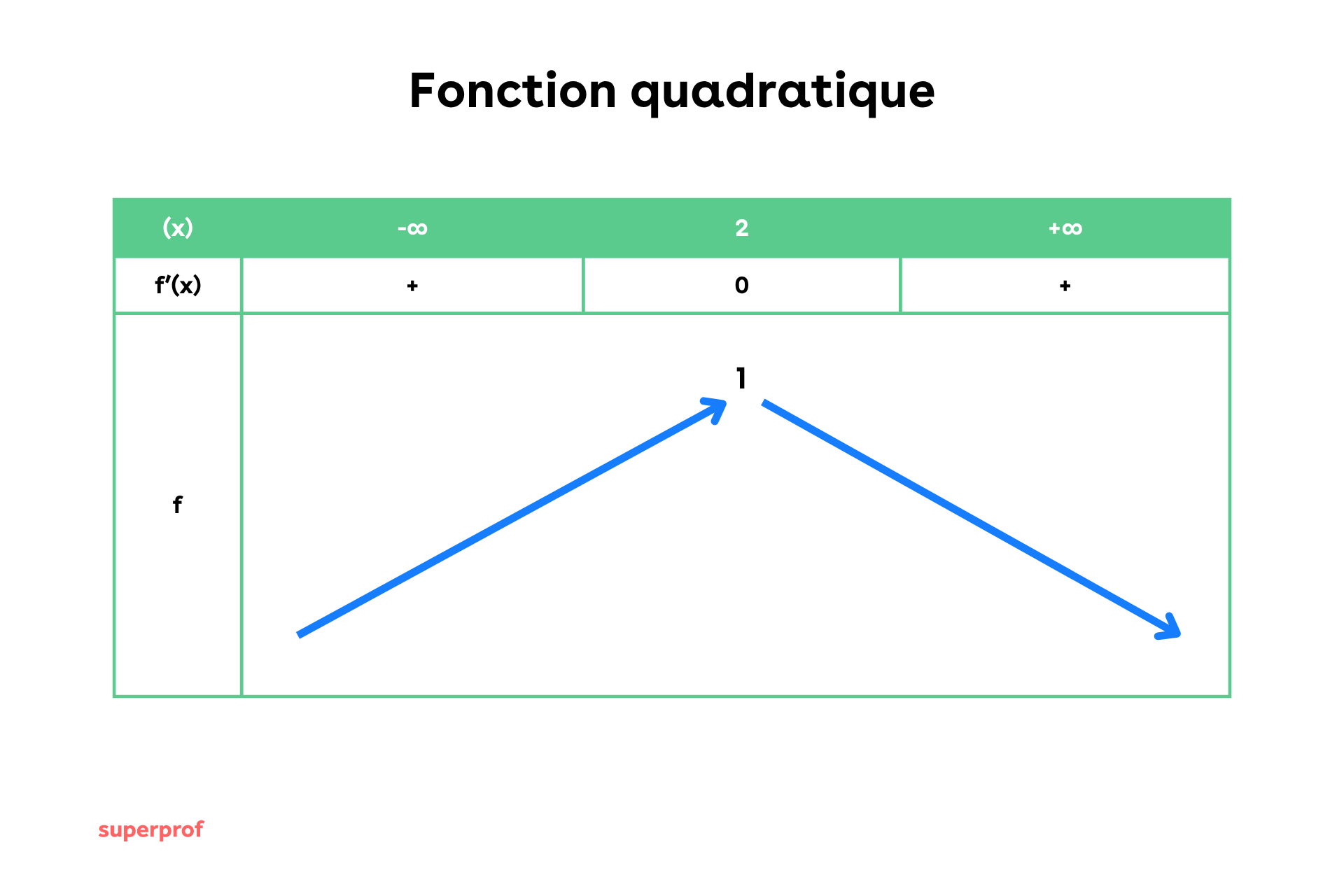
La fonction est croissante sur (−∞, 2) et décroissante sur (2, +∞).
Exemple 2 : la fonction polynomiale de degré supérieur
Reprenons notre exemple 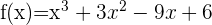 sur l'intervalle
sur l'intervalle 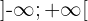 .
.
1️⃣ La dérivée est 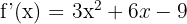
2️⃣ Pour étudier le signe de ce polynôme du second degré, on factorise. On remarque que 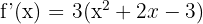 . Pour factoriser ce trinôme il faut tout d'abord calculer le discriminant et trouver les racines x1 et x2. On calcule le discriminant
. Pour factoriser ce trinôme il faut tout d'abord calculer le discriminant et trouver les racines x1 et x2. On calcule le discriminant 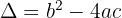 pour le trinôme
pour le trinôme 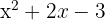 , ce qui nous donne les racines
, ce qui nous donne les racines 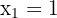 et
et 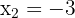 . La forme factorisée est donc
. La forme factorisée est donc 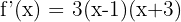 . Le tableau de signes de f'(x) est le suivant :
. Le tableau de signes de f'(x) est le suivant :
| x | - ∞ | -3 | [-3 ; 1] | 1 | +∞ |
|---|---|---|---|---|---|
| x + 3 | - | 0 | + | + | |
| x - 1 | - | - | 0 | + | |
| f'(x) | + | 0 | - | 0 | + |
3️⃣ Les extremums : On a déjà calculé 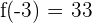 (maximum local) et
(maximum local) et 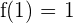 (minimum local).
(minimum local).
4️⃣ On obtient le tableau de variation final :
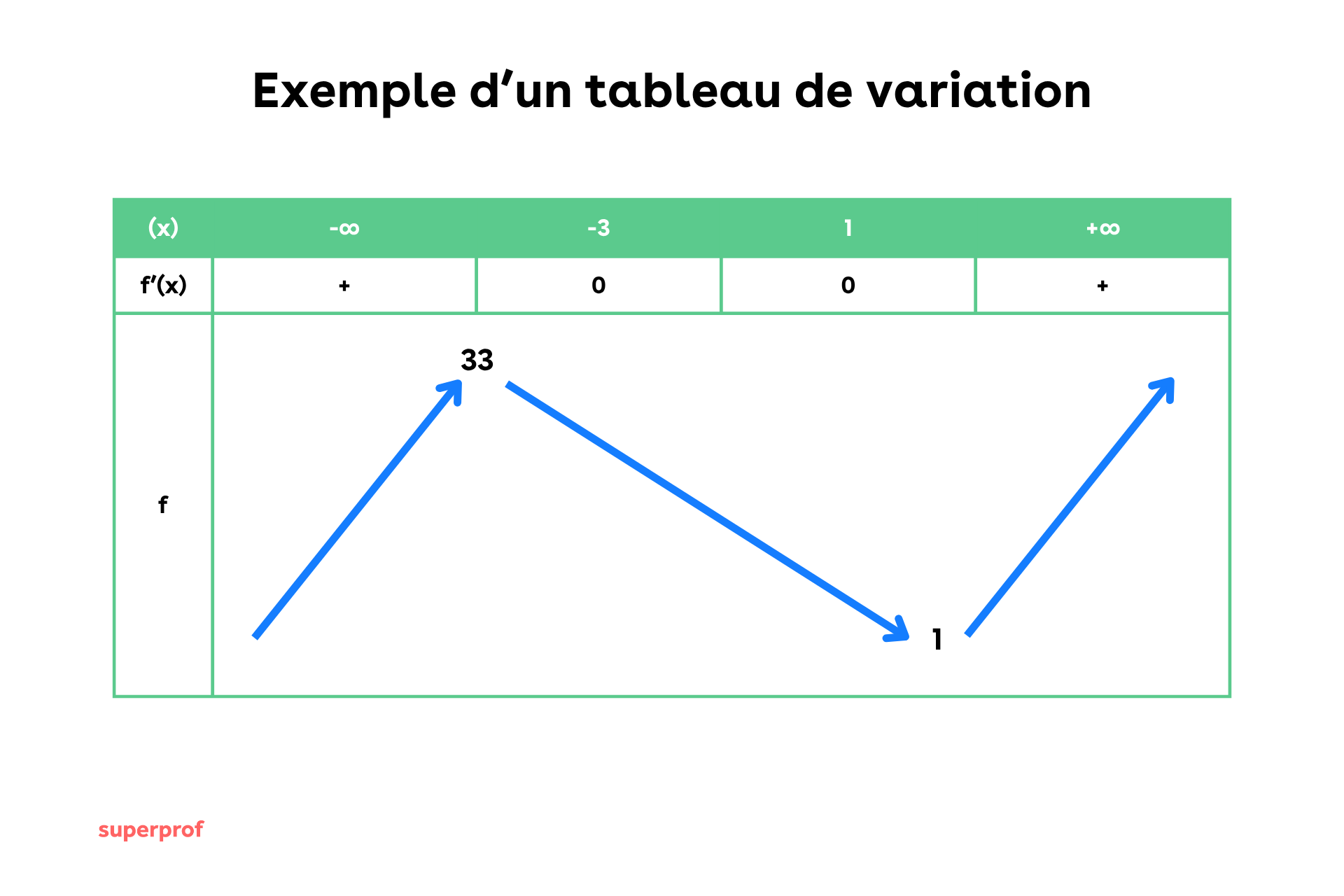
Les erreurs courantes et nos conseils pour éviter les pièges
Attention car il est facile de se tromper quand on s'attaque au tableau de variation. Comme toujours en cours de maths, il est indispensable d'être attentif !
Les erreurs dans le calcul de la dérivée
On a listé trois erreurs courantes que vous pouvez faire dès le calcul de la dérivée.
1️⃣ Vous pouvez d'abord oublier qu'une constante à une dérivée nulle.
Si 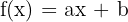 , alors
, alors 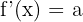 car
car 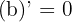 .
.
Exemple : 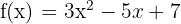 alors
alors 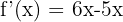 et pas
et pas 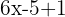 .
.
Vous pourriez être tenté de dériver 7 en 1 ou de garder +7 dans f'(x).
2️⃣ Vous pouvez également vous tromper dans les formules produit et quotient.
Pour le produit 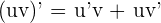 , avec
, avec 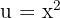 et
et 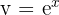 :
:
✅ Ce qui est correct : 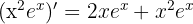
❌ L'erreur fréquente : avec un oubli du second terme ou (double erreur).
Pour le quotient 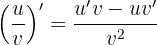 , avec
, avec 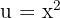 et
et 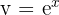
✅ Ce qui est correct : 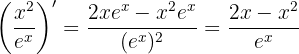
❌ L'erreur fréquente est de calculer 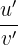 ou de calculer
ou de calculer 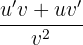 .
.
Mémorisez u’v — uv’ sur v². L'ordre et le signe "moins" sont importants.
3️⃣ Vous pouvez enfin faire des erreurs de signe en dérivant des termes comme 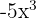 . N'oubliez pas que
. N'oubliez pas que 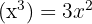 et que le signe "-" devant le monôme se conserve.
et que le signe "-" devant le monôme se conserve.
✅ Ce qui est correct : 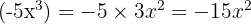
❌ L'erreur fréquente : vous oubliez le signe - et le -15 se transforme en 15 ou vous appliquez la mauvaise règle de puissance.
Et oui la factorisation, c'est comme résoudre une énigme mathématiques en cours de maths.
Pour un produit, dites à voix haute: “d’abord je dérive u, puis v; puis je garde u, je dérive v; et j’additionne”.
Pour un quotient, écrivez d’emblée le dénominateur au carré v2 , puis remplissez le numérateur “u’v − uv’”.
Une mauvaise interprétation du signe de la dérivée
L'erreur la plus fréquente est de confondre le signe de la fonction  avec celui de sa dérivée
avec celui de sa dérivée  .
.
C'est le signe de  qui donne les variations de
qui donne les variations de  .
.
- Si
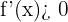 sur un intervalle alors
sur un intervalle alors  y est croissante
y est croissante - Si
 sur un intervalle alors
sur un intervalle alors  y est décroissante.
y est décroissante.
Un exemple piégeux :
 peut être négative tout en étant croissante (ex : de −10 à −2, la fonction “monte” car les valeurs augmentent).
peut être négative tout en étant croissante (ex : de −10 à −2, la fonction “monte” car les valeurs augmentent).- Ce comportement se lit dans
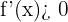 , indépendamment du signe de
, indépendamment du signe de  .
.
Faites deux tableaux distincts si besoin :
un tableau de signes pour f'(x) (zéros, intervalles de +/−),
puis le tableau de variation pour f(x) (↗/↘ et extremums).
Maîtriser le tableau de variation d'une fonction en cours de mathématiques permet de vous faire gagner des points lors du contrôle continu : ce n'est donc pas un chapitre du programme de maths à négliger !
Et si vous preniez des cours particuliers pour étudier d'autres aspects des maths ? Tangente, axe des abscisses, fonction définie ou cosinus : autant de thèmes à aborder pendant un cours de maths en ligne !
Résumer via IA :
















Je l’aimais beaucoup ce cours
J’ai beaucoup apprécié ce cours !
Je vraiment aimé ce cours merci beaucoup et j’aimerais davantage sur ce DM svp comment procéder à cette fonction de dérivée ci dessous ?
Soit la fonction f(x) = 2×3+5×2-4x + 1, définie sur [-100 ; 100],
Dériver f(x),
Étudier le sens de variation de la fonction dérivée,
f(x) est-elle croissante sur [-100 ; -50] ?
Dresser un tableau de variation de la fonction,
Tracer la représentation graphique de la fonction f.
Merci bien le cours est bien complet. Sinon, un cours des valeurs approchées ?
Quelle est la méthode pour dresser un tableau de variation d’une fonction exponentielle ? Faut-il déterminer les racines ou bien les limites ?
cela dépend de ton intervalle mais ce sont souvent les limites qui sont demandées
Bonsoir,
J’ai pu me remémorer les sens de variation d’une fonction que j’avais oubliés.
Merci.
Le cours était parfait
Bonjours comment faire pour dresser le tableau de variation lorsque la dérivée est f'(x)= -2x+10-8/x ? La fonction de départ est f(x)= -2x+10x-9-8ln(x)
Bonjour Céline,
Il faut commencer par étudier le signe de f'(x) en cherchant à savoir quand f'(x) s’annule. Une fois cette information trouvée, il vous sera plus simple de dresser le tableau de variation et de chercher ses limites.
Si vous avez besoin d’aide, n’hésitez pas à faire appel à un professeur particulier sur Superprof. Une application peut également vous aider dans ce cas : SnapSchool. Il vous suffit de poster votre problème pour trouver de l’aide auprès d’autres élèves.
Bon courage et bonne réussite !
Bonjours pouvez vous m’aider pour établir un tableau de variations ?
Bonjour,
Vous pouvez demander de l’aide à l’un de nos professeurs en mathématiques. Pour cela, regardez les profils présents dans votre région et contactez-les après inscription. Si vous êtes mineur, il faudra donc voir cela avec vos parents.
Vous pouvez également demander de l’aide à votre professeur de mathématiques.
Bien à vous
cours interressant
Comment établir le tableau de variation ??
cours interressant wesh
cool
je suis vraiment content de ce contenu
bonjour, comment dresser le tableau avec une dérivée égale à g'(x)= 3x(2+x)
merci :)
Bonjour,
Même conseil que pour Céline: commencez par étudier le signe de g'(x) en cherchant à savoir quand g'(x) s’annule.Vous pourrez ensuite trouver le tableau des variations et les limites.
L’aide d’un professeur particulier pourra éventuellement vous être utile pour l’aide aux devoirs. Faites également un petit tour sur l’application « SnapSchool » pour trouver l’aide de vos camarades.
Bonne continuation
Bonjour, pourriez vous me dire comment dresser le tableau de variations de la fonction suivante svp ? :
f(x) = x-1/x avec un intervalle I = tous les réels sauf 0
Bonjour,
L’article ci-dessus vous donne toutes les clefs et les étapes pour dresser le tableau de variations de votre fonction.
Bon courage
Salut pouvez vous m’aider ?
Bonjour,
Merci pour votre commentaire, en quoi pourrions-nous vous aider ?
Bien à vous
merci beaucoup pour ces cours cest tres interessant pour les eleves merci pour vos efforts
Grâce à ce cours, j’ai pu approfondir l la notion de tableau de variation.
Vraiment j’aime beaucoup la façon d’expliquer et j’ai compris après votre explication
Bonjour,
Merci pour votre commentaire.
Bien à vous
Cela ne pas aider pour mon devoir de math mais merci quand mème.
Moi mes problèmes sont: tableau de signe et variation et étude de la variation d’une.
Merci cette source inépuisable.
Quelle est la méthode pour dresser un tableau de variation d’une fonction intrvalle ?