Entre beauté et complexité, le nombre Pi incarne l'élégance des mathématiques: on n'affirme pas, on démontré!
Faisant partie des constantes les plus célèbres des mathématiques où l'on y trouve également 0, e, i, π est un nombre fascinant qu’on retrouve dans les cercles, les ondes, et bien plus encore.
a une valeur approximative de
3,14159
Le nombre Pi est un nombre irrationnel qui continue donc indéfiniment. Utilisé dans de nombreux calculs géométriques, notamment pour calculer l'aire et le volume de cercles ou de boules, il est également utilisé en physique, en ingénierie ou encore même dans le domaine de la finance.
Aussi appelé, constante d'Archimède, Pi exerce une fascination sans limite depuis sa découverte dans l'Antiquité. Il est même entré dans la culture populaire.
est la journée de célébration du nombre pi.
Nous faisons le point sur le nombre Pi, sa signification et ses usages, ce que vous pourrez également retrouver lors de cours de maths seconde.
La définition du nombre Pi 📚
Tout comme le nombre imaginaire i défie notre intuition en mathématiques, le nombre π intrigue par sa présence constante dans les cercles et les formules.
Le nombre Pi désigne le rapport constant entre la circonférence d'un cercle et son diamètre.
Le nombre Pi se définit également comme le rapport de l'aire d'un disque mis au carré de son rayon.
La lettre π a été choisie en 1647 par l'Anglais William Oughtred (1574-1660), d'après le nom grec περίμετρος, qui signifie périmètre au XVIIIème siècle.
Il s'agit de l'une des constantes les plus importantes et les plus utilisées en mathématiques.
Le nombre π intéresse les scientifiques depuis plus de 4 000 ans et son histoire est longue et pas encore finie. Vous voulez en apprendre plus sur Pi et vous avez envie d'une apprentissage personnalisé avec un cours de math ? N'hésitez pas à contacter l'un de nos profs.
Pour découvrir un peu plus sur cet univers mystérieux du nombre Pi, un petit podcast :
L'histoire du nombre Pi 📖
Dès l'Antiquité, les mathématiciens étaient persuadés qu'il était possible de calculer un rapport constant entre le périmètre du cercle et le diamètre de celui-ci. Ils pensaient qu'il existait parallèlement un rapport entre l'aire du disque et le carré de son rayon.
2000 av. n. è.
Une tablette babylonienne
découverte en 1936 estime le nombre π à 3+1/8, soit 3,125
1650 av. n. è.
Le papyrus Rhind
donne une approximation de π de 3.1605
VIIIème siècle av. n. è.
Sulbasutras (Inde)
donnent une approximation de π à 3.088
IIIème siècle av. n. è.
Archimède
trouve les limites inférieurs et supérieurs de π
Vème siècle
Zu Chongzi
estime le nombre pi à 7 décimales
Une des plus célèbres approximations de π a été retrouvée dans le papyrus Rhind, publié par le scribe Ahmès (vers 1540 avant J-C).
L'aire du cercle de diamètre 9 coudées est celle du carré de côté 8 coudées.
Il trouvait alors, au milieu du second millénaire avant notre ère, que π prenait la valeur (16/9)², soit 3,16.
Le papyrus Rhind est conservé au British Museum, à Londres et nous offre une incroyable perspective des connaissances mathématiques en Egypte ancienne.
En 1936, des archéologues ont retrouvé des tablettes de Babylone, rédigées en écriture cunéiforme et datant de 2 000 ans avant notre ère, représentant des calculs d'aire d'une valeur de π faisant 3+1/8, soit 3,125.
Au IIIe siècle avant J-C, le célèbre penseur Archimède (-287;-212) établit que le rapport de la surface d'un disque au carré de son rayon est égal au rapport de son périmètre à son diamètre.
On avait déjà utilisé des polygones pour calculer la circonférence d'un cercle avant, mais Archimède est le premier à trouver les limites de Pi grâce au polygones circonscrits et inscrits, en augmentant le nombre de côtés.
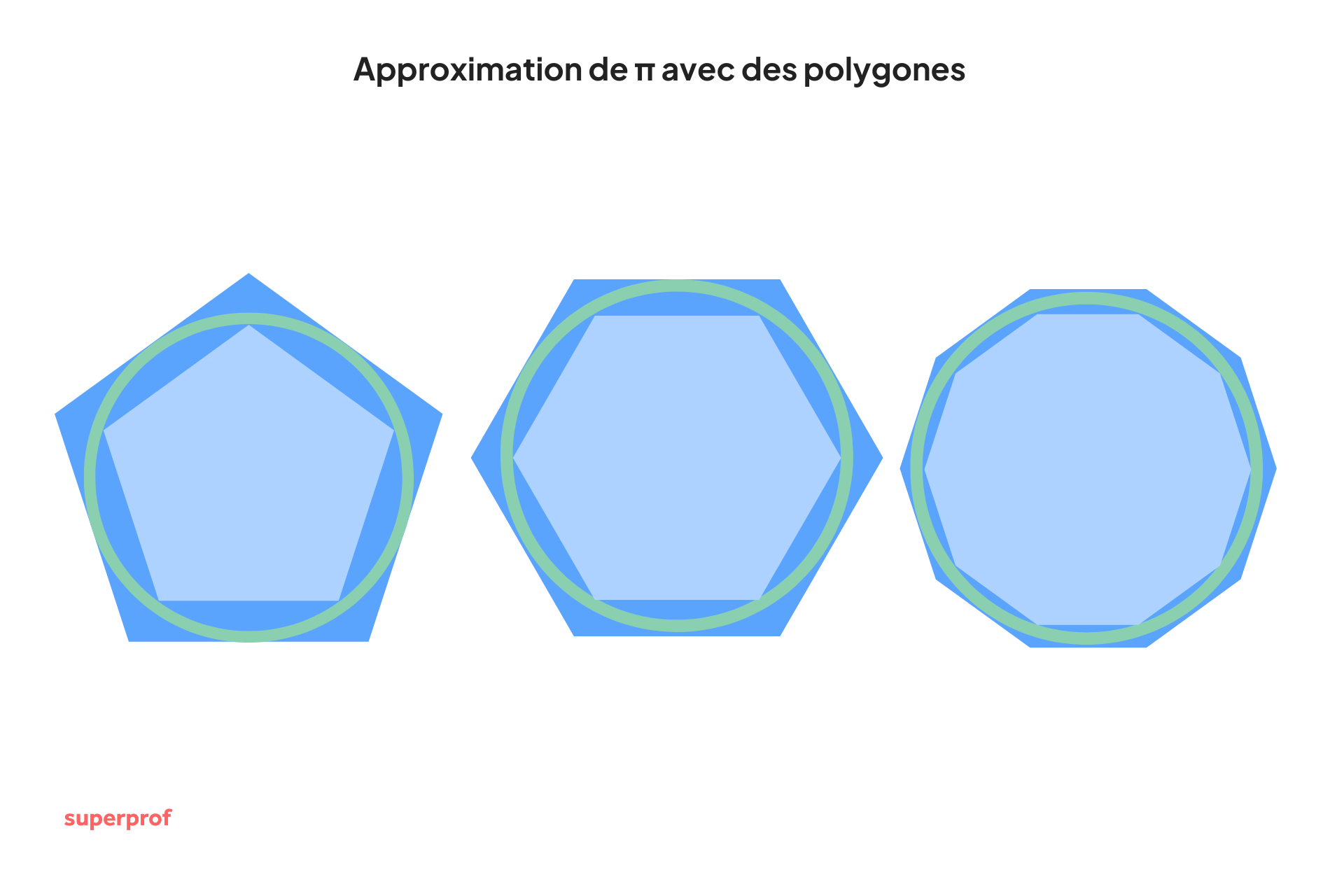
La méthode d'Archimède avec des polygones à 192 côtés, puis 3072 côtés sera utilisée en Chine pour trouver une approximation de π au cent-millième (c'est-à-dire à 5 décimales). Si l'on rajoute des dodécagones (polygones à 12 côtés) inscrits et circonscrits on précise encore plus la valeur de π.
Au Ve siècle de notre ère, le savant Chinois Tsu Chung Chih (430-501) parvient à trouver une approximation au millionième près, à 3,141592 et ensuite ce sera le tour des mathématiciens Arabes qui calculent des approximations de π à 14 décimales exactes.Il faudra attendre la fin du XVIe siècle pour que les savants occidentaux ne parviennent à trouver des avancées concrètes sur ce nombre.
1593
Françoi Viete (FR)
trouve une approximation à 9 décimales
1596
Ludolph van Ceulen
publie le livre Van den Circkel dans lequel il trouve 20 décimales au nombre π en utilisant la méthode d'Archimède .
La période moderne et la Renaissance provoque une explosion culturelle, des progrès techniques rapides ainsi qu'une accélération sans précédent des recherches scientifiques.
C'est l'époque où de grands mathématiciens marqueront l'histoire grâce à leurs travaux : Isaac Newton (1642-1727), Gottfried Wilhelm von Leibniz (1646-1716), John Machin (1680-1751), James Stirling (1692-1770).
C'est le célèbre mathématicien Leonhard Euler (1707-1783), par ailleurs connu pour ses progrès dans la connaissance du nombre e, qui fera s'imposer définitivement le caractère spécial π pour désigner le nombre Pi.
Les formules prennent alors la forme de calculs infinis et très performants.
Ainsi celles-ci se complexifient au fil des siècles, jusqu'à la prouesse de l'Indien Srinivasa Ramanujan (1887-1920).
L'une de ses formules, trouvée en 1910, par exemple :
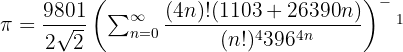
Sa formule permet de calculer π avec 8 décimales.
Grâce à ses apports multiples, la connaissance des décimales après la virgule de π a connu une croissance exponentielle à la fin du XXe siècle.
de décimales de Pi calculées en 75 jours. Cette entreprise de stockage américaine a dû utiliser 36 dispositifs de stockage SSD pour stocker au total environ 1 pétaoctet (un million de giga-octets) de données.
Ca donne presque le tournis, non ? Tout d'un coup, un cours de maths en ligne parait moins challengeant.
Comment représenter le nombre Pi ? ✏️
Il est assez difficile d'envisager qu'on ne connaisse pas toutes les décimales d'un nombre, comme si celui-ci pouvait être infini.
Vous savez sans aucun doute que l'écriture décimale de la valeur approchée de Pi est environ égale à 3,1416, parfois même simplifiée à seulement 3,14.
3,14159265358979323846264338327950288419716939937510582
On retient donc souvent, pour simplifier, que π = 3,14.
La valeur approchée de π retient 22 septièmes ou racine de 10.
En réalité, au niveau de connaissances de l'année 2013, les chercheurs et mathématiciens avaient trouvé plus de 12 mille milliards de décimales de Pi. Même si, dans la vie quotidienne, estimer la circonférence d'un cercle ne nécessite pas plus d'une dizaine de décimales de Pi.
En 1881, Simon Newcomb a démontré qu'il suffisait de 10 décimales de Pi pour calculer la circonférence de la Terre et de trente pour obtenir celle de l'univers visible.
👉 Si vous connaissez déjà les 15 premières décimales de Pi, vous serez bien plus avancé que la majorité de vos amis : 3,141 592 653 589 793.
Pi reste un mystère pour les scientifiques et fascinent professionnels et amateurs qui essaient d'en savoir toujours davantage sur ce nombre. Encore aujourd'hui, des recherches sont menées pour en apprendre plus sur le nombre Pi.
Pourquoi le nombre Pi est-il irrationnel et algébrique ? 👩🏫
Pi, un nombre irrationnel
On dit que le nombre Pi est un nombre irrationnel. Cela signifie que π s'écrit avec un nombre infini de décimales sans suite logique.
On entend souvent dire que π est un nombre "irrationnel". Mais qu’est-ce que cela veut dire, concrètement ? Tout simplement qu’on ne peut pas l’écrire sous forme d’une fraction, c’est-à-dire comme le rapport de deux nombres entiers. En d’autres termes, il est impossible d'e trouver des entiers d'écrire π = p/q où p et q sont entiers.
Prenons un autre exemple célèbre :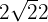 
. C’est le nombre qu’il faut multiplier par lui-même pour obtenir 2. Là encore, impossible de l’écrire comme une fraction simple. Ce type de nombre échappe à notre manière "classique" de représenter les quantités.
Concernant π, les mathématiciens soupçonnaient déjà depuis le IXe siècle qu’il ne pouvait pas être rationnel, mais il faudra attendre 1768 pour qu’un certain Jean-Henri Lambert le prouve formellement. Sa démonstration repose sur un outil mathématique un peu technique : le développement en fraction continue de la fonction tangente.
Plus tard, d’autres mathématiciens ont repris ce travail pour le simplifier. L’une des démonstrations les plus élégantes reste celle d’Ivan Niven, qui utilise uniquement le calcul intégral.
Quant à la question de savoir si π peut être la racine carrée d’un autre nombre rationnel — comme √π ≠ x²=π — on sait depuis les travaux de Ferdinand von Lindemann (1852-1939) que ce n’est pas le cas. Il a en effet prouvé que π est non seulement irrationnel, mais aussi transcendant : il ne peut pas être solution d’une équation polynomiale à coefficients entiers. Rien que ça !
Trouvez votre cours de math 3eme ici.
La transcendance du nombre π
Au-delà du fait d'être irrationnel, le nombre Pi est aussi transcendant, c'est-à-dire qu'il n'est pas algébrique : il n'y a aucun polynôme (à coefficient rationnel) dont Pi soit la racine.
Ce résultat a été démontré au XIXe siècle, en 1873. Charles Hermite (1822-1901), mathématicien Français, parvient à prouver que la base du logarithme népérien, le nombre e, est transcendant.
En 1882, Ferdinand von Lindermann généralise ce raisonnement, et développe le théorème d'Hermite-Lindermann.
Selon ce dernier, si x est un algébrique différent de 0, alors ex est transcendant. Or eiπ est algébrique car il est égal à -1.
Alors, iπ est transcendant. Sachant que i est algébrique, π est transcendant. De plus, il a été démontré que Pi n'est pas constructible. C'est une conséquence importante de la démonstration de la transcendance de π. Et si vous arriviez déjà en cours de maths terminale s avec ces connaissances? Ce n'est pas tout!
A quoi sert le nombre Pi ? 🔍
Pi ne sert pas uniquement à affoler les élèves de collège qui doivent apprendre quelques formules pour calculer le périmètre et l'aire d'un cercle.
Le nombre Pi est utilisé depuis l'Antiquité par les mathématiciens, d'abord pour résoudre des problèmes géométriques, puis dans le calcul intégral et enfin à l'ère informatique pour calculer toujours davantage de décimales de Pi.
Pi apparaît naturellement lorsqu’on étudie les cercles, car il représente le rapport constant entre la circonférence d’un cercle et son diamètre, quelle que soit sa taille. Ce nombre est essentiel en géométrie, mais aussi en physique et en ingénierie, car on le retrouve dans de nombreuses formules scientifiques.
Le rôle de π en géométrie
Comme nous le mentionnons précédemment les formules de géométrie impliquant Pi concernent les cercles et les sphères.
On peut calculer la circonférence d'un cercle de rayon r et de diamètre d. Mais aussi plusieurs aires :
Aire d'un disque,
Aire d'une ellipse de demi-axes,
Aire d'une sphère,
Aire latérale d'un cylindre,
Aire latérale d'un cône.
Volume d'une boule,
Volume d'un cylindre,
Volume d'un cône,
Volume d'un tore.
Le nombre Pi dans les probabilités et les statistiques
Les probabilités et les statistiques ne dérogent pas à la règle : Pi est partout ! Il est utilisé par exemple dans la loi normale d'espérance et d'écart type mais aussi dans la loi de Cauchy. Des mathématiciens ont utilisé π dans des expériences de probabilité. Les probabilité peuvent servir à obtenir une approximation de Pi. C'est notamment le cas de l'expérience intitulée l'aiguille de Buffon.
Cette méthode présente ces limites en ne permettant d'obtenir que quelques décimales de Pi.
Les autres utilisations du nombre Pi
Le nombre Pi est aussi utilisé en mathématiques dans des formules avec :
- Des nombres complexes,
- Des suites récursives,
- Des suites logistiques,
- Des séries,
- Des intégrales.
Comme quoi, le nombre Pi est omniprésent en mathématiques et pas seulement dans les formules de mathématiques impossibles à retenir ! Pi est aussi présent partout dans notre quotidien :
Dans le mécanisme d'une horloge, les dents des engrenages dessinent une ronde parfaitement synchronisée. Leur espacement, calculé grâce au nombre π, garantit que le temps s’écoule sans accroc, tic après tac.
L’électricité qui alimente nos appareils suit un rythme ondulant, comme une respiration. Ce courant alternatif dessine des vagues mathématiques, les fameuses sinusoïdes, où le nombre π impose la cadence.
Sur la route, π est discret mais essentiel. Le compteur de vitesse se base sur les tours de roue, eux-mêmes liés au périmètre, et donc à π, explique Jean-Paul Delahaye. C'est ainsi que nous mesurons notre allure.
Et si parmi la liste d'usages on trouverait quelque chose qui nous aiderait dans les cours de maths 1ere s? La liste des usages de Pi est encore longue, très longue - et la probabilité que ceci soit vrai, haute !
Comment calculer le nombre Pi ? 🧮
Connaître des centaines et des centaines de décimales après 3,1415, apprendre l'histoire du nombre π est intéressant, mais alors, comment peut-on calculer réellement π et tendre vers sa valeur exacte ? Pour approfondir ces méthodes, pensez aux cours particuliers maths disponibles à Marseille.
Comme l'on a déjà vu, on peut retenir plusieurs méthodes pratiques pour approcher à quelques chiffres après la virgule une approximation du nombre π, notamment:
1. Le calcul de Pi à partir des mesures d'un cercle
Méthode :
- Vérifier que tous les points soient à égale distance du centre (que ce soit un cercle),
- Mesurer le périmètre du cercle,
- Mesurer le diamètre du cercle,
- Utiliser la formule de la circonférence (C=π²d). Vous obtiendrez π = C/d,
- Vérifier le résultat avec des cercles de périmètres différents, calculer la moyenne des résultats trouvés.
2. Calculer Pi en utilisant une série infinie
Méthode :
Avec la formule de Leibniz-Gregory ((4/1)-(4/3)+(4/5)-(4/7)+...) : alterner additions et soustractions de fractions avec 4 au numérateur et un nombre impair croissant au dénominateur. Plus le calcul sera long et plus vous aurez une valeur précise de π,
Avec la formule de Nilakantha : alternance d'additions et de soustractions de fractions avec 4 pour numérateur. Le dénominateur est un produit de 3 entiers.
La méthode de Buffon
Georges-Louis Leclerc de Buffon est un mathématicien Français du XVIIIe siècle.
En 1733, il réalise une expérience de probabilités avec des aiguilles jetées sur un parquet, lui permettant d'obtenir une approximation de la valeur de π.
L'expérience consistait à lancer un très grand nombre de fois une aiguille sur un parquet.
La probabilité que l'aiguille tombe à cheval sur au moins une rainure du parquet serait égale au nombre Pi.
Buffon comptabilise pour cela le nombre de fois où l'aiguille tombait à cheval sur une rainure du parquet, par rapport au nombre total de lancers.
Au fur et à mesure que le nombre de lancers augmente, le quotient se rapproche d'un certain nombre permettant de retrouver π.
3. Calcul de Pi avec la fonction arcsinus
Méthode :
- Choisir un nombre x dans l'intervalle [-1;1],
- Remplacer le nombre choisi dans la formule 2*[arcsin (sqrt (1-x^2)) + abs (arcsin(1))].
Voici quelques explications en image :
Faut-il mémoriser le nombre Pi ? 🧠
La mémorisation du nombre Pi tourne à l'obsession chez de nombreuses personnes.
- Daniel Tammet, autiste Asperger a récité 22 514 décimales en 2004.
- Ce record est battu en 2005 par Lu Chao, qui a mémorisé et récité 67 890 décimales.
énoncées par l'indien Rajveer Meena en 2015. Cette performance est enregistrée au Guinness des Records.
Si vous voulez tenter de retenir un maximum de décimales de π, il existe plusieurs méthodes, dont la mémorisation d'un poème dont le nombre de lettres de chaque mot correspond à une décimale (un mot de 10 lettres vaut 0). Voici les premiers vers :
Que j’aime à faire apprendre un nombre utile aux sages ! (3,1415926535)
Glorieux Archimède, artiste, ingénieur, (8979)
Toi de qui Syracuse aime encore la gloire, (32384626)
Soit ton nom conservé par de savants grimoires ! (43383279)
Dans l'utilisation normale que l'on peut faire de Pi, il n'y en revanche aucune raison de mémoriser un maximum de décimales du chiffre. A part pour épater ses amis ! 😁
Vous connaissez désormais tous les secrets du nombre Pi !
Vous avez aimé cet article ? Notez-le !
Loading...
une sphère peut elle avoir pi comme rayon ?
Bonjour,
Bien entendu, le rayon peut avoir n’importe quelle valeur. Cependant, il s’agira de la forme raccourci de Pi.
Bien à vous
vous avez une vidéo dessu
Merci beaucoup
De rien mon amour
YAAAAAA BAKAAAAA
Archimède a étudié en Egypte, donc en afrique le PI est dans toutes les constructions des pyramides … Aristote, Thalès, ^Platon , etc, etc ont tous appris en Egypte. Chez les Nubiens donc. Pour infos
Petite coquille…
Vous écrivez :
Le diamètre du tronc est donc de 28,33 centimètres : π/89 = 28,33.
C’est l’inverse 89/Pi=28,33…
Bonjour,
Effectivement, merci pour votre retour. Cela est corrigé.
Bien à vous
Ohhh ma PuPuce merci beaucoup
J’ai trouvé une explication qui détermine
Pi c’est le nombre de l’expansion
Sphérique de l’univers
Article très comolet
Article Intéressant et accessible sur le nombre Pi