Tant que les lois mathématiques renvoient à la réalité, elles ne sont pas absolues, et tant qu’elles sont absolues, elles ne renvoient pas à la réalité.
Albert Einstein
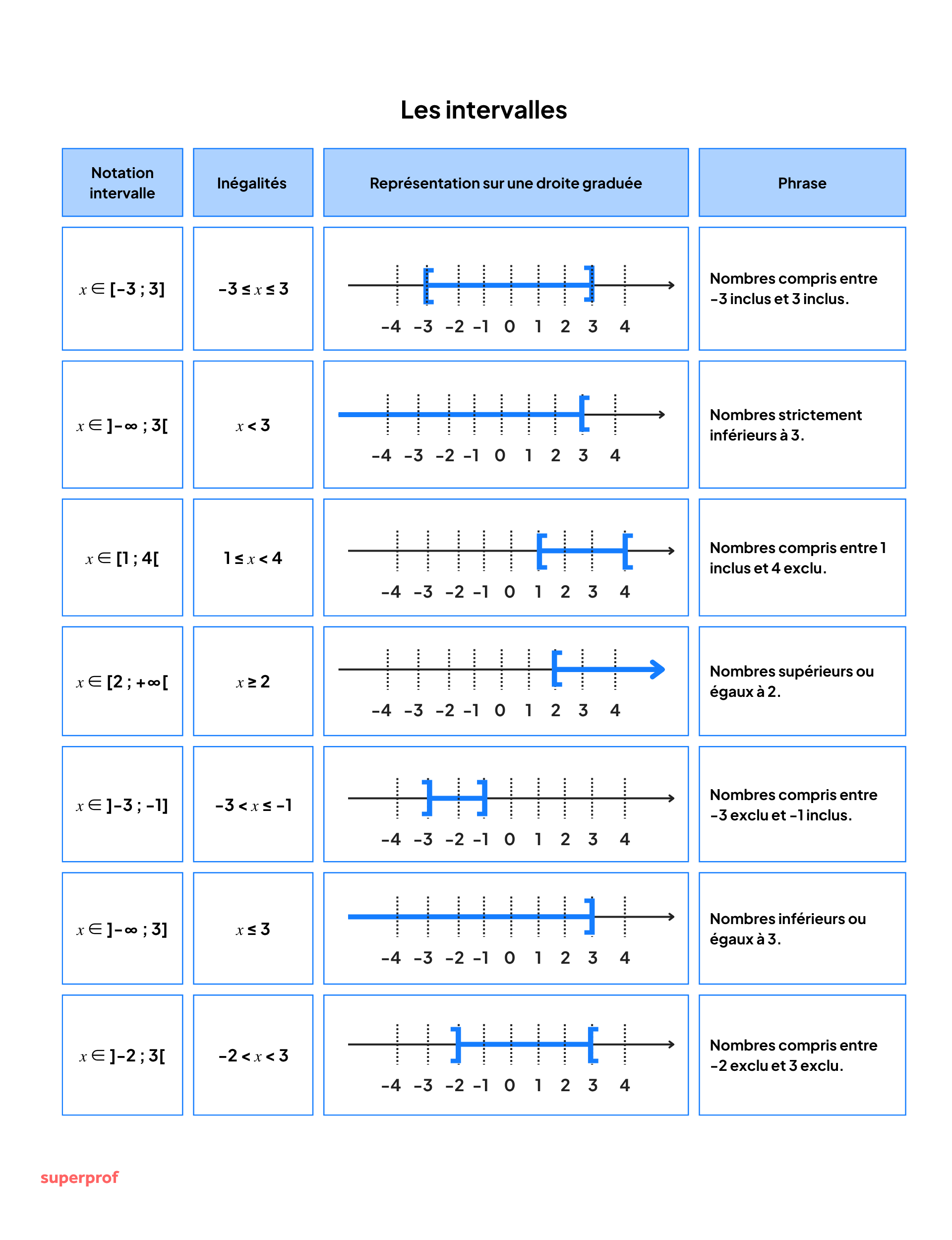
Un intervalle est un ensemble de nombres réels entre deux bornes, notées avec crochets selon que les bornes sont incluses ou non.
Pour calculer la longueur d'un intervalle, il faut faire borne supérieure – borne inférieure. Exemple : [3 ; 7] → longueur = 4.
Les intervalles occupent une place fondamentale dans de nombreux domaines scientifiques et techniques.
En statistiques
Ils permettent de quantifier l’incertitude autour d’une estimation grâce aux intervalles de confiance, essentiels pour interpréter la fiabilité des résultats et prendre des décisions éclairées.
En analyse de fonctions et en mathématiques
Les intervalles servent à décrire des ensembles de valeurs, à étudier la continuité ou la croissance d’une fonction, et à structurer la topologie de la droite réelle.
Dans les sciences expérimentales et l’ingénierie
Ils facilitent la mesure précise de grandeurs physiques (température, temps, distance) et l’analyse des marges d’erreur, contribuant ainsi à la rigueur des protocoles.
Grâce à leur capacité à encadrer des valeurs et à exprimer des marges d’incertitude, les intervalles sont donc des outils incontournables pour modéliser, comparer et interpréter des données dans des contextes variés.

Définition et notation des intervalles
Qu’est qu’un intervalle ?
Petit rappel de vos cours de math de seconde : on parle d’un intervalle pour désigner un ensemble, c’est-à-dire tous les éléments compris entre deux valeurs et donc compris dans l’intervalle.
Admettons un ensemble des réels R, ou si vous préférez une droite graduée de chiffres réels. On appelle intervalle l’ensemble des nombres réels compris entre deux réels positifs ou réels négatifs a et b, ou de la même façon l’ensemble des points de la droite dont la marque est entre a et b.
Prenons pour exemple l’intervalle [4 ; 6]
Il désigne l’ensemble des réels x tels que 4 ≤ x et x ≤ 6.
Sont donc compris dans l’intervalle les nombres positifs 4, 5 et 6, x étant plus grand que 4 et plus petit ou égal à 6.
On distingue plusieurs types d’intervalles que nous détaillerons un peu plus loin :
- L’intervalle borné ou intervalle fermé,
- L’intervalle ouvert,
- L’intersection entre deux intervalles ou plus,
- La réunion d’intervalles.
Voyons maintenant comment un mathématicien applique les intervalles avec des nombres positifs et négatifs d’un ensemble défini, des chiffres après la virgule et différents ensembles.
Notation des intervalles : comment les écrire ?
En cours de maths, les bornes de l’intervalle sont mentionnées avec des crochets.
On distingue les intervalles ouverts ] a ; b [ , les intervalles fermés [a ; b] et les intervalles semi-ouverts [a ; b [ et ] a ; b].

Pour écrire les bornes, il faut suivre un ordre mathématique : l’ordre croissant, c’est-à-dire d’abord la borne inférieure puis la borne supérieure. Il ne faut jamais écrire de manière décroissante, car cela serait illogique.
Quand les crochets sont fermés, cela signifie que chaque borne appartient à l’intervalle.
Quand les crochets sont ouverts, cela signifie que les bornes n’appartiennent pas à l’intervalle.
| Notation d'intervalle | Inégalités correspondantes | Phrase |
|---|---|---|
| 𝑥 ∈ [-3 ; 5] | -3 ≤ 𝑥 ≤ 5 | Ensemble des nombres compris entre -3 inclus et 5 inclus. |
| 𝑥 ∈ ]-∞ ; 3[ | 𝑥 < 3 | Ensemble des nombres strictement inférieurs à 3. |
| 𝑥 ∈ [4 ; 6[ | 4 ≤ 𝑥 < 6 | Ensemble des nombres compris entre 4 inclus et 6 exclu. |
| 𝑥 ∈ [2 ; +∞[ | 𝑥 ≥ 2 | Ensemble des nombres supérieurs ou égaux à 2. |
| 𝑥 ∈ ]-3 ; -1] | -3 < 𝑥 ≤ -1 | Ensemble des nombres compris entre -3 exclu et -1 inclus. |
| 𝑥 ∈ ]-∞ ; 5] | 𝑥 ≤ 5 | Ensemble des nombres inférieurs ou égaux à 5. |
| 𝑥 ∈ ]-2 ; 5[ | -2 < 𝑥 < 5 | Ensemble des nombres compris entre -2 exclu et 5 exclu. |
En revanche, il ne faut pas confondre les intervalles avec les ensembles de nombres qui s’écrivent en utilisant les accolades. Par exemple, voici l’ensemble des nombres entiers {0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9}. Il comprend donc tous les chiffres de 0 à 9 inclus.
Pour désigner des ensembles abstraits, il faut les écrire sous la forme de lettres. Cette notation est emprunté au calcul littéral. Quand vous calculez des intervalles, vous retrouverez fréquemment ceux que nous vous avons référencés ici :
- N désigne l’ensemble des entiers naturels
- Z désigne l’ensemble des entiers relatifs
- D désigne l’ensemble des nombres décimaux
- Q désigne l’ensemble des nombres rationnels (c’est-à-dire les nombres qui peuvent s’écrire sous forme de quotient de deux nombres entiers relatifs)
- R désigne l’ensemble des réels
- I désigne l’intersection de deux ensembles
- U désigne l’union de deux intervalles.
En cours de math en ligne, vous rencontrerez également des signes mathématiques pour désigner deux ensembles de nombres réels et leur interaction.
Le différents types d'intervalles
Il existe différents types d'intervalles : ouverts, fermés, semi-ouverts mais aussi bornés ou non bornés. Dans cette partie, on vous explique également les concepts d'intersection et de réunion d'intervalles, ainsi que les inéquations, les inégalités et la valeur absolue.
Les intervalles ouverts, fermés, semi-ouverts
Un intervalle peut être ouvert, fermé ou semi-ouvert (ouvert d'un côté et fermé de l'autre).
Un intervalle ouvert ]a ; b[
Il n'inclue pas les bornes
Par exemple : ]2 ; 7[ signifie que l'intervalle contient l'ensemble des nombres compris entre 2 exclu et 7 exclu (soit -1, 1, 2, 3, 4, 5 et 6).
Un intervalle fermé [a ; b]
Il inclue les bornes
Par exemple : [-1 ; 1] signifie que l'intervalle contient l'ensemble des nombres compris entre -1 inclus et 1 inclus (soit -1, 0 et 1).
Un intervalle semi-ouvert [a ; b[ ou ]a ; b]
Il inclue une borne et exclue l'autre
Par exemple : [1 ; 4[ signifie que l'intervalle contient l'ensemble des nombres compris entre 1 inclus et 4 exclu (soit 1, 2 et 3). Autre exemple : ]-2 ; 2] signifie que l'intervalle contient l'ensemble des nombres compris entre -2 exclu et 2 inclus (soit -1, 0, 1 et 2).
Les intervalles bornés et non bornés
Les intervalles bornés
Il contient les bornes de l’intervalle, soit les points qui le bornent. On peut le noter de différentes manières en admettant deux réels a et b tels que x est l’ensemble des réels tels que :
- [a ; b] = a ≤ x ≤ b,
- [a ; b[ = a ≤ x < b,
- ] a ; b] = a < x ≤ b,
- ] a ; b [= a < x < b.
En cours de maths, quand les crochets sont fermés, x est supérieur ou égal à a et inférieur ou égal à b. Si les crochets sont ouverts, x est strictement supérieur à a et strictement inférieur à b.
Les intervalles non bornés
Soient a et b différents nombres :
- [a ; ∞[= x ≥ a,
- ] a ; ∞[= x > a,
- ] - ∞ ; b] = x ≤ b,
- ] - ∞ ; b [= x < b.
On parle d'intervalle non borné quand une des bornes est l'infini.
On ne sait pas où commence ou où finit l'intervalle.
L’intersection des intervalles
L’intersection des intervalles [a ; b] et [c ; d] est l’ensemble x des réels compris à la fois dans [a ; b] et [c ; d]. On note alors l’intersection par le signe arrondi « inter » ∩.
Soit a, b, c et d quatre nombres entiers positifs tels que l’intersection I entre ces deux intervalles se note de deux façons équivalentes : I=[a ; b] ∩ [c ; d] ou I=[c ; d] ∩ [a ; b].
Par exemple : 2 ∈[0 ; 5] ∩[2 ; 6] car 2 ∈[0 ; 5] et 2 [2 ; 6].
Pour déterminer l’intersection de deux intervalles, l’idéal est de représenter un ensemble sur une droite réelle. Ainsi, vous verrez directement comment se place chaque élément et ce qui est commutatif, c’est-à-dire les éléments qui forment un ensemble.
La réunion d’intervalles
Il s’agit de l’ensemble des nombres réels x qui est soit dans l’intervalle [a ; b] soit dans l’intervalle [c ; d]. L’union se note avec le signe ∪.
Soit a, b, c et d quatre nombres imaginaires tels que l’union U entre ces deux intervalles se note :
U = [a ; b] ∪ [c ; d] ou U=[c ; d] ∪ [a ; b]
Par exemple : 2 ∈[0 ; 5] ∪ [2 ; 6] car 2 ∈[0 ; 5] 3,8 ∈[0 ; 5] ∪ [2 ; 6] car 3,8 ∈[0 ; 6].
Pour déterminer l’intersection de deux intervalles, on représente les deux intervalles sur un axe gradué et on repère l’ensemble de chiffres du premier intervalle plus l’ensemble des nombres du deuxième intervalle.
Les inéquations
Pour cette possibilité, il faut retenir que l’ensemble solution d’une inéquation est toujours un intervalle ou un ensemble vide.
Une inéquation d’inconnu x est une expression de la forme : A (x) ≤ B(x) ou A(x)<B(x) où x est une variable inconnue.
Résoudre l’inéquation, c’est trouver toutes les valeurs de x pour lesquelles l’inégalité est satisfaite : l’ensemble de ces réels x est alors appelé l'ensemble des solutions de l’inéquation. On dit que deux inéquations sont équivalentes lorsqu’elles ont le même ensemble de solutions.
Voici les transformations possibles sur les inéquations pour les transformer en inéquation équivalente :
- Ajouter ou soustraire un même nombre non nul aux deux membres,
- Multiplier ou diviser les deux membres par un même nombre positif non nul,
- Multiplier ou diviser les deux membres par un même nombre négatif non nul,
- Développer, factoriser ou réduire les membres.
Les inégalités
Pour les inégalités, il y a trois règles à connaître.
La première est que l'on peut ajouter ou soustraire un même nombre à chaque membre d’une inégalité : si a ≤ b, alors a + c ≤ b + c.
La deuxième est que l'on peut ajouter membre à membre deux inégalités de même sens : si a ≤ b et c ≤ d, alors a + c ≤ b + d.
Et enfin la troisième est que l'on peut multiplier ou diviser chaque membre d’une inégalité par un même nombre non nul, à condition de changer le sens de l’inégalité si ce nombre est négatif.

La valeur absolue
La valeur absolue d’un nombre réel x est la distance entre le point O et le point M d’abscisse x sur une droite graduée.
Retenez que la distance entre deux réels a et b est la distance des points A d’abscisse a et B d’abscisse b sur une droite graduée.
Cela paraît un peu compliqué et abstrait au premier abord, mais vous verrez avec de la pratique que les intervalles sont très simples à utiliser.
Ils sont la retranscription arithmétique d’un énoncé.
Ils permettent par exemple, grâce à un schéma de départ sous forme de cercle ou de droite graduée, de visualiser une donnée mathématique. Et grâce au schéma vous pourrez très rapidement visualiser comment interagissent plusieurs intervalles ensemble.
Répétez les exercices pour assimiler correctement tous les éléments et caractères utilisés pour écrire des intervalles. C'est ainsi que vous pourrez gagner du temps et calculer beaucoup plus vite.
Pour finir sur l’écriture des intervalles, voici un tableau récapitulatif des signes utilisés pour les exprimer :
| Signes mathématiques | Significations |
|---|---|
| ∈ | Appartient |
| ∉ | N’appartient pas |
| ∞ | Ensemble infini |
| ∩ | Intersection |
| ∪ | Union |
| ≠ | Pas égal à |
| ≤ | Inférieur ou égal |
| ≥ | Supérieur ou égal |
| < | Strictement inférieur |
| > | Strictement plus grand |
Maintenant que vous êtes incollable sur la retranscription des intervalles tels les grands mathématiciens, grâce à un ensemble d’exemples, voyons dans la partie suivante comment ces symboles mathématiques sont utilisés pour écrire un intervalle.
D’ordinaire, une vie s’inscrit entre deux nombres qui délimitent le parcours terrestre, l’entrée et la sortie, à charge de celui-là, l’évoqué mathématique, de résoudre cette équation pleine d’inconnu que pose l’entre-deux.
Jean Rouaud

Les formules et calculs des intervalles
Voyons maintenant comment résoudre un intervalle. Ne vous inquiétez pas, il suffit de bien lire l’énoncé et de poser un schéma pour visualiser ce qui contient un ensemble, ce qui fait parti de l’ensemble ou ce qui en est exclu.

Si vous avez bien compris comment lire les signes mathématiques, vous devriez réussir facilement.
Le calcul de la longueur d'un intervalle
Pour calculer la longueur d'un intervalle, il suffit d'appliquer la formule mathématique suivante : longueur = borne supérieure – borne inférieure.
Par exemple, la longueur de l'intervalle [3 ; 7] est de 4 en appliquant la formule : 7 - 3 = 4.
Les intervalles de tolérance et de confiance
L'intervalle de tolérance et l'intervalle de confiance sont utilisés en statistiques.
L'intervalle de tolérance est un intervalle dans lequel on s’attend à trouver une proportion donnée de la population, avec un certain niveau de confiance.
Un intervalle de tolérance sert à dire : « Je suis sûr à X % que Y % des valeurs de la population se trouvent entre ces deux bornes. »
Autrement dit, il ne s’agit pas d’un intervalle de confiance (qui concerne un paramètre comme la moyenne), ni d’un intervalle de prédiction (qui concerne une valeur future), mais bien d’un intervalle qui englobe une fraction de la population.
Imaginons qu’on mesure le diamètre de 100 pièces de monnaie.
On veut déterminer un intervalle [a ; b] tel que :
- au moins 95 % de toutes les pièces produites ont un diamètre entre a et b,
- avec 99 % de confiance.
→ On parle alors d’un intervalle de tolérance bilatéral (99 %, 95 %).
Cela signifie qu’on est sûr à 99 % que 95 % des diamètres réels sont compris entre a et b.
L'intervalle de confiance est une estimation statistique qui sert à encadrer un paramètre inconnu d’une population (par exemple, une moyenne ou une proportion) à partir d’un échantillon.
Quand on fait un sondage ou une mesure sur un échantillon, on obtient une estimation (comme une moyenne ou un pourcentage). Mais cette estimation n’est jamais exacte : elle dépend de l’échantillon choisi.
L’intervalle de confiance permet donc de dire : « Je suis confiant à X % que la vraie valeur dans la population se trouve entre ces deux bornes. »
| Type d'intervalle | Ce qu'il encadre | Exemple |
|---|---|---|
| Intervalle de tolérance | Une fraction de la population | « 95 % des valeurs sont entre 9,7 et 10,3 avec 99 % de confiance. » |
| Intervalle de confiance | Un paramètre (moyenne, proportion…) | « Je suis sûr à 95 % que la vraie moyenne est entre 9,8 et 10,2. » |
Les applications pratiques des intervalles
Les intervalles sont omniprésents en mathématiques. Qu’il s’agisse de représenter des données, d’estimer des paramètres ou de décrire le comportement d’une fonction, ils constituent un outil essentiel pour exprimer des valeurs comprises entre deux bornes.
En statistiques : la représentation des données et les estimations
En statistiques, les intervalles permettent de résumer et d’interpréter des informations issues d’un échantillon.
On les retrouve notamment dans :
Les intervalles de confiance, qui encadrent un paramètre inconnu de la population (comme une moyenne ou une proportion) avec un certain niveau de confiance.
Les intervalles de prédiction, qui estiment la zone probable dans laquelle une future observation tombera.
Les intervalles de tolérance, qui définissent les bornes à l’intérieur desquelles se situe une proportion donnée de la population.
Ces outils facilitent la prise de décision et l’évaluation de la fiabilité des résultats, que ce soit en sondage, en contrôle qualité ou en recherche scientifique.
En analyse de fonctions : étude des domaines de définition et d’image
En analyse, les intervalles servent à délimiter les ensembles de valeurs sur lesquels une fonction est définie ou prend certaines valeurs.
- Le domaine de définition d’une fonction correspond souvent à un ou plusieurs intervalles du réel.
- L’image ou ensemble des valeurs possibles de la fonction se décrit également à l’aide d’intervalles, surtout lors de l’étude des variations.
Ainsi, les intervalles permettent de modéliser le comportement global d’une fonction et de visualiser ses bornes, que ce soit pour tracer son graphe, étudier sa continuité ou résoudre des inégalités.
Nous espérons que cet article vous aura fait réviser les grandes notions propres aux intervalles. Comme vous l’aurez compris, en mathématiques on utilise des nombres réels allant de -∞ à +∞. La plupart du temps on aimerait s’intéresser qu’à une partie de ces nombres. C’est que les intervalles rentrent en jeu pour déterminer les chiffres appartenant à l’ensemble ou à contrario ceux qui en sont exclus.
Pour aller plus loin
- Monka, Yvan. Nombres réels et intervalles. Académie de Strasbourg, https://www.maths-et-tiques.fr/telech/19NombresReels2M.pdf. Consulté le 13 octobre 2025
- Université Côte d’Azur. Image des intervalles. Cours d’analyse, https://math.univ-cotedazur.fr/~ah/ens/cours/anal12/thmcont.pdf. Consulté le 13 octobre 2025
- Revol, Nathalie. Introduction à l’arithmétique par intervalles. INRIA / ENS Lyon, https://perso.ens-lyon.fr/nathalie.revol/polys/ArithIntervalles.pdf. Consulté le 13 octobre 2025
Résumer via IA :















Il faudrait faire des représentations de ces schémas
En vrai la représentation elle est importante 🙌
Sur super prof j’arrive à me débrouiller en math troisième
C’est vraiment incroyable ce que vous faites merci beaucoup et bon courage
Est -ce que vous ne donnez pas d’exercice
Salut comment allez vous
Parfait
Je veux rejoindre de vos cours
C’est une cours intéressant
Bonjour ! Merci pour votre intérêt. N’hésitez pas à contacter nos professeurs particuliers pour aller plus loin dans votre apprentissage sur le sujet ! Bonne journée. :)
Merci pour tout. À l’avenir ajoutez des schémas
Bonjour Loriane, merci pour votre suggestion ! Bonne journée !
Attention, il y a une erreur dans la deuxième ligne des intervalles bornés !
A corriger ;)
Bonjour Christophe,
Merci pour votre vigilance ! Nous allons vérifier et corriger l’erreur mentionnée. Votre retour nous aide à améliorer nos contenus.
À bientôt sur Superprof !
Merci beaucoup pour cette grande révision super proff.
J’ai 90 ans et je viens de comprendre les intervalles, ce qui n’existait pas de mon temps, je suppose que cela est dù aux maths modernes.. Merci pour cet exposé très clair.. Je suis ing.techn.