Chapitres
Connaissez-vous les entiers naturels ? Evidemment puisque ce sont les premiers nombres que l'on découvre quand on est enfant. Il s'agit des nombres "pleins" et sans virgule tels que 0, 1, 2, 3, 4, 5, etc. On les note ℕ.
On les utilise tous les jours dans la vie quotidienne pour une action tellement simple que l'on n'en a même pas conscience : compter. On appelle cela dénombrer. C'est l'usage que l'on fait des premiers nombres depuis l'Antiquité pour représenter une quantité. On peut s'en servir pour compter des objets comme "Il y a 5 boîtes" ou encore des personnes "Nous serons 4 demain".
Les entiers naturels servent également à ordonner et classer des éléments. Vous en avez des exemples très simples à rencontrer au quotidien : situer une maison ("j'habite au numéro 20"), ordonner des participants à un concours ("les 100 premiers seront reçus") ou encore organiser une liste ("la piste n°3 du CD").
Pour finir, on trouve aussi les entiers naturels dans les outils d'identification. C'est le cas avec les numéros de téléphone, les numéros de sécurité sociale ou encore les plaques d'immatriculation.
Il est important de noter que les ordinateurs aussi utilisent les entiers naturels avec leurs algorithmes, notamment en utilisant le système binaire composé de 0 et de 1.

Qu’est-ce qu’un nombre entier naturel ?
Nombre entier naturel : définition
Comme évoqué précédemment, les entiers naturels se regroupent dans un ensemble que l'on note ℕ. Il se constitue de tous les nombres entiers à partir de 0 jusqu'à l'infini : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ..., +∞.
Il existe aussi l'ensemble ℕ* qui est presque exactement le même que ℕ mais avec une différence notable : le zéro n'en fait pas partie : 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ..., +∞.
Notations et symboles des nombres entiers naturels
Nous avons déjà vu les symboles ℕ et ℕ* pour désigner les entiers naturels avec ou sans zéro. Cette notation ℕ est utilisée en abréviation de "naturel".
Mais il existe également l'ensemble ℤ que l'on appelle l'ensemble des entiers relatifs. Le Z provient de l'abréviation de Zahlen qui signifie "Nombres" en allemand. Les entiers relatifs sont les nombres entiers comme les nombres entiers naturels sauf qu'eux possèdent un signe (positif ou négatif). Ils désignent donc les nombres entiers entre -∞ et +∞, zéro inclus : -∞, ..., -11, -10, -9, -8 , -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ..., +∞.
De l'ensemble ℤ découlent trois autres ensembles : ℤ*, ℤ+ et ℤ-. Pour ℤ*, vous l'aurez deviné, cela représente les entiers relatifs sans le zéro. En ce qui concerne ℤ+, il s'agit des entiers relatifs positifs, donc tous les entiers relatifs sans signe - , et zéro inclus. Pour ℤ-, c'est le même principe mais uniquement les entiers relatifs négatifs donc sans signe +, toujours avec le zéro inclus.
Si dans la convention française, l'ensemble ℕ contient le zéro, dans les pays anglo-saxons, l'ensemble ℕ exclut le zéro.
Afin de clarifier les choses, l'Organisation Internationale de Normalisation a tranché, c'est la convention française qui a raison ! (norme ISO 80000-2)
Comprendre les opérations et propriétés des entiers naturels
Opérations arithmétiques de base
Sur les entiers naturels, on peut effectuer diverses opérations : les additions, les soustractions, les multiplications et aussi certaines divisions (dites partielles).
Pour l'addition et les multiplications, c'est le plus simple. En effet, les opérations effectuées par addition et multiplication avec des entiers naturels donnent toujours des entiers naturels. On dit de ces opérations qu'elles sont internes à ℕ.

En ce qui concerne la soustraction et la division, les choses sont un peu différentes. Tout d'abord, toutes les opérations de soustraction ne sont pas possibles dans ℕ. Pour que la soustraction existe dans ℕ, il faut que dans l'opération a - b, a soit supérieur ou égal à b. C'est pour cette raison qu'ont été inventés les entiers relatifs. Pour finir, en ce qui concerne la division, seules les divisions euclidiennes (aussi appelées divisions partielles) sont possibles.
Pour réaliser une division euclidienne, il y a une méthode : on cherche combien de fois un nombre (le diviseur) est présent dans un autre (le dividende). La formule officielle est : Dividende = Diviseur x Quotient + Reste avec Reste < Diviseur.
Voici quelques exemples simples pour chacune d'entre elles :
Addition
5 + 3 + 2 = 10 ou 3 + 2 + 5 = 10
Elle est dite commutative car on peut changer l'ordre des nombres additionnés.
Multiplication
10 x 2 = 20
1 x 150 = 150
0 x 49 = 0
Dans cette opération, l'élément neutre est 1 et l'élément absorbant est 0.
Soustraction
L'opération 25 - 10 = 15 est possible dans ℕ tandis que 20 - 30 n'est pas possible dans ℕ. On dit que la réponse n'est pas définie dans cet ensemble.
Division euclidienne
Dans certains cas, le résultat tombe juste :
10 ÷ 2 = 5
Dans d'autres, il y aura un reste :
14 ÷ 3 = 4 reste 2 qui s'écrit 14 = 3 x 4 + 2.
Propriétés fondamentales
Avec ces opérations sur les nombres entiers naturels, quelques propriétés sont à connaître. Nous en avons détaillé quelques-une dans les exemples précédents. Il y a trois règles fondamentales : l'associativité, la commutativité et l'élément neutre.
Commençons par l'associativité. C'est une règle qui dit qu'une fois qu'il y a plus de 3 nombres impliqués dans une addition ou une multiplication, alors on peut changer l'ordre et la place des parenthèses. Cela peut vous aider à résoudre plus facilement des équations.
Par exemple, calculer l'opération (8 + 4) + 4 revient à résoudre 8 + (4 + 4) qui est plus facilement faisable de tête. Cela donne 16.
Vient ensuite la commutativité. Cette règle nous dit que l'on peut échanger la place des nombres dans les additions et les multiplications sans en changer le résultat. Là aussi le but est de faciliter les calculs. Par exemple, de tête, on calculera plus facilement 49 + 3 que 3 + 49, alors que le résultat est toujours 52.
Pour finir, on retrouve la règle de l'élément neutre. Il s'agit d'un nombre dont la présence ne change rien au résultat. Pour l'addition, il s'agit du 0 et pour la multiplication il s'agit du 1. En effet, peu importe le nombre x que l'on ajoute à 0, le résultat sera toujours x. De même quand on multiplie, n'importe quel nombre multiplié par 1 sera toujours lui-même.
Voici un tableau récapitulatif des formules associées à chacune de ces règles :
| Règle | Formules associées |
|---|---|
| Assertivité | Addition : a + b = b + a Multiplication : a x b = b x a |
| Commutativité | Addition : (a + b) + c = a + (b + c) Multiplication : (a x b) x c = a x (b x c) |
| Élément neutre | Addition : a + 0 = a Multiplication : a x 1 = a |
Attention, dans l'ensemble ℕ, les entiers naturels n'ont pas d'inverse !
Les relations avec d'autres ensembles de nombres
Entiers relatifs
Nous avons déjà évoqué rapidement les entiers relatifs au début de cet article. Pour rappel, il s'agit des nombres entiers positifs et négatifs. Leur ensemble se note ℤ.
Leur naissance vient du constat que nombre d'opérations de soustractions étaient impossibles dans ℕ car si l'on cherche à soustraire un nombre b supérieur à un nombre a alors il n'y a pas de solution dans ℕ. (3 - 5 n'a pas de solution dans ℕ par exemple). C'est là que les entiers relatifs sont apparus, comme "miroirs" des nombres naturels, avec un symbole - devant. Ainsi, toutes les soustractions de nombres entiers sont maintenant possibles.
ℤ ne vient pas remplacer ℕ mais au contraire, il l'englobe. On dit que ℕ est inclus dans ℤ et cela se note ℕ ⊂ ℤ.
Nombres rationnels et réels
Après avoir réglé le problème des soustractions avec l'ensemble ℤ, reste le problème des divisions.
En effet, dans ℤ, la division n'est possible que dans de rares cas. Dès que l'on essaie de diviser un nombre par un autre plus grand que lui, alors il n'y a pas de solution.
C'est là que sont apparues les fractions, ainsi que l'ensemble qui y est attaché, l'ensemble ℚ. Il contient tous les nombres qui peuvent s'écrire sous forme de fraction a / b. Son nom Q vient de "quotient" et on appelle ces nombres les nombres rationnels.
Grâce à ce nouvel ensemble, on a maintenant une solution pour exprimer les nombres à virgule finis (comme 0,6) mais aussi les nombres à virgule infinis dits périodiques, dont la fin se répète (comme 0,333...). Pour finir, on peut dire que l'ensemble ℤ est contenu dans ℚ.

Maintenant que le problème des fractions est réglé, il reste néanmoins des nombres que l'on ne peut pas représenter. C'est le cas par exemple des racines. Prenons par exemple √2. On ne le trouve pas dans ℕ, ℤ ou encore ℚ. C'est donc là que les nombres irrationnels se sont révélés nécessaires. Ils sont contenus dans l'ensemble ℝ et sont appelés les réels. Pour se représenter les choses, on peut dire que sur une droite graduée, les réels représentent absolument toutes les valeurs, même celles avec une infinité de chiffres après la virgule sans logique. On y retrouvera par exemples les racines ou π.
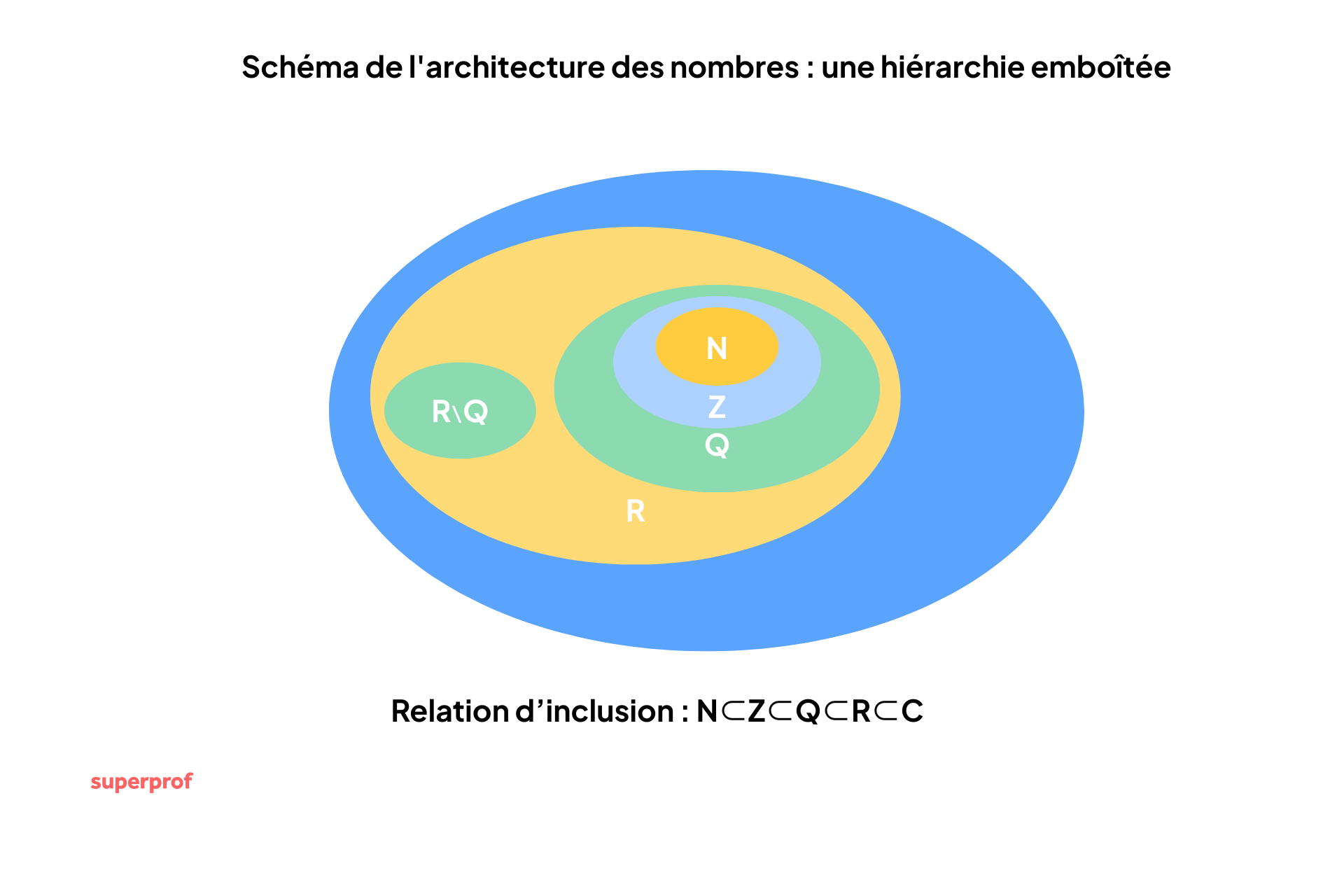
Pour vous aider à mieux comprendre, voici comment les ensembles évoqués précédemment sont inclus les uns dans les autres :
ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ
À quoi servent les entiers naturels ?
Applications mathématiques des entiers naturels
Les entiers naturels peuvent paraître simples et uniquement servir dans des opérations simples de la vie. Mais c'est une erreur ! Ils ont une place irremplaçable dans le fonctionnement des mathématiques dites discrètes.
Prenons par exemple l'arithmétique. Il s'agit de la spécialité des mathématiques dans lesquelles on étudie les propriétés des nombres entiers. On utilise donc uniquement l'ensemble ℕ. Plusieurs règles de base des mathématiques en découlent, comme les nombres premiers. Saviez-vous que chaque entier naturel supérieur à 1 est soit premier lui aussi soit produit unique de nombres premiers ?
Ces fameux nombres premiers sont encore utilisés de nos jours dans de nombreux domaines comme la cryptographie bancaire.
Les nombres entiers naturels sont aussi utiles pour la combinatoire. Il s'agit d'une branche des mathématiques qui sert à étudier les façons de compter et organiser. C'est ce que l'on utilise par exemple en informatique ou en probabilités. Dans les outils importants de la combinatoire, on retrouve par exemple la factorielle, le principe de Dirichlet ou encore les combinaisons.
Pour mieux comprendre, voici des exemples de chacun de ces outils :
- La factorielle : Il y a 3 élèves dans la classe et 3 chaises disponibles. Il existe 6 possibilités différentes. Cela se calcule avec la formule suivante : 3! = 3 × 2 × 1 = 6 ;
- Le principe de Dirichlet : Si vous êtes un groupe de 25 copains, alors il y aura forcément au moins deux copains qui sont nés le même mois car une année ne compte que 12 mois ;
- La combinaison : 2 élèves sont choisis par le professeur parmi 5 pour faire un exercice. Alors l'ordre de choix n'a pas d'importance, le groupe (A, B) est le même que le groupe (B, A) quand on le regarde dans son ensemble.
Pour finir, les entiers naturels permettent de mesurer les infinis. Un ensemble est dit dénombrable quand on peut numéroter ses éléments avec des entiers naturels. C'est ce que l'on appelle la cardinalice.
Dans les algorithmes aussi les entiers naturels sont une base incontournable. Prenons le raisonnement par récurrence. Si on place des dominos en ligne et que le premier (P0) fait tomber le deuxième (P1). Alors si on prouve qu'un domino tombe, alors tous les suivants tomberont. Cela donne la formule suivante : P(n)⟹P(n+1).
Vous avez sûrement déjà travaillé autour de l'Algorithme d'Euclide. Ce dernier est utilisé en mathématiques pour calculer le PGCD (Plus Grand Commun Diviseur). Dans cet algorithme aussi, ce sont les entiers naturels qui entrent en jeu.
Il y a aussi le raisonnement de la descente infinie, décrit par le mathématicien Pierre de Fermat, qui utilise les entiers de ℕ. Voici son principe : dans N, il n'existe pas de suite strictement décroissante infinie. On ne peut pas descendre sous zéro. Cela prouve que si on suppose qu'une solution existe et que l'on montre qu'on peut toujours en construire une plus petite, alors on aboutit à une contradiction. Pour en savoir plus, vous pouvez regarder la vidéo du professeur Yvan Monka sur les PCGD et PPCM :
Exemples concrets d’utilisation dans la vie quotidienne
Dans notre vie quotidienne, la plupart des utilisations des nombres entiers naturels revient à des fonctions d'identification. Par exemple, les adresses IP, les codes-barres dans les magasins, les codes postaux ou encore les ISBN pour les livres.
Ces numéros servent juste à identifier et l'on n'effectue jamais de calcul dessus.
Mais les nombres entiers naturels servent aussi pour trier des éléments (ce que l'on appelle les entiers ordinaux). C'est le cas des tickets pour passer à la boucherie dans la file d'attente, des classements des meilleurs lycées de France ou encore des versions de mise à jour de votre smartphone !
Mais il ne faut pas oublier l'un des usages les plus fréquents des nombres entiers naturels dans notre société moderne : l'informatique. En effet, les ordinateurs ne communiquent qu'en binaire : des 0 et des 1. Mais pour leur parler, on utilise des lettres qui sont gérées dans des genres d'alphabets comme l'Unicode ou l'ASCII. Ces derniers associent chaque lettre à un entier naturel, par exemple un A est représenté par 65. Pour finir, les couleurs de l'ordinateur sont définies par le système appelé RGB (Red, Green, Blue pour Rouge, Vert, Bleu) qui permet de décrire jusqu'à 16 777 216 couleurs différentes en donnant un code pour chacune des couleurs compris entre 0 et 255.

Exercices sur les nombres entiers naturels
À vous de jouer pour vérifier votre compréhension des différentes entiers. Sortez votre brouillon et testez vos connaissances avec ces exercices.
Cherchez l'intrus.
Parmi la liste de nombres suivante, identifiez ceux qui appartiennent à l'ensemble des entiers naturels ℕ :
- 15
- - 4
- 0
- 8,5
- 12 / 3
- √25
- π
- 15 : OUI. C'est un entier positif classique.
- - 4 : NON. C'est un entier négatif, il appartient à ℤ.
- 0 : OUI. C'est le premier entier naturel (dans la convention française).
- 8,5 : NON. C'est un nombre décimal (à virgule).
- 12 / 3 : OUI. Attention au piège. Même s'il est écrit sous forme de fraction, 12 ÷ 3 = 4. Or, 4 est bien un entier naturel.
- √25 : OUI. Attention au piège. √25 = 5. C'est un entier naturel caché.
- Pi (π) : NON. C'est un nombre irrationnel (environ 3,14...), il appartient à ℝ.
Vrai ou Faux ?
Pour chaque affirmation, dites si elle est Vraie ou Fausse. Si elle est fausse, donnez un contre-exemple.
- La soustraction de deux entiers naturels est toujours un entier naturel.
- Tous les entiers naturels sont aussi des nombres rationnels (ℚ).
- Si je multiplie un entier naturel par lui-même, le résultat est toujours positif.
- FAUX. Si l'on calcule 5 − 10, on obtient −5. Ce n'est plus dans ℕ, mais dans ℤ.
- VRAI. Tout entier n peut s'écrire sous la forme de fraction 1n. Donc ℕ est inclus dans ℚ.
- VRAI. Un entier naturel est positif. Un positif multiplié par un positif donne toujours un positif (+ × + = +).























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Trouble le plus petite entire naturel admettant 6 diviseurs? 8? 12?