Chapitres
- 01. Introduction
- 02. Qu’est-ce qu’une division euclidienne ?
- 03. Comment faire une division euclidienne ?
- 04. L'égalité euclidienne : la formule magique pour vérifier
- 05. Propriétés et applications de la division euclidienne
- 06. Exercices pratiques sur la division euclidienne
- 07. Flashcards : Vrai ou Faux ?
Introduction
La division euclidienne est une notion fondamentale en mathématiques, enseignée dès l'école primaire et approfondie au collège, notamment en classe de 6ème et de 3ème. Mais attention, ne vous y trompez pas : bien qu'elle semble simple, elle constitue la base de concepts bien plus complexes utilisés dans des domaines variés comme l'arithmétique avancée, les algorithmes informatiques ou encore la cryptographie (sécurité des données bancaires, par exemple).
Alors, de quoi parle-t-on exactement ? Contrairement à la division "classique" que vous faites sur une calculatrice et qui vous donne un nombre à virgule, la division euclidienne s'intéresse aux nombres entiers. C'est l'histoire d'un partage équitable où l'on garde ce qui ne peut plus être partagé.
Exemple rapide pour comprendre :
Imaginez que vous avez 14 bonbons à distribuer équitablement à 4 enfants.
- Chaque enfant recevra 3 bonbons.
- Il restera 2 bonbons dans votre main.
- Mathématiquement, cela s'écrit :
.
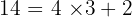Dans cet article complet, nous allons vous proposer une explication claire, progressive et illustrée pour comprendre la division euclidienne, apprendre à la poser, maîtriser son vocabulaire et vérifier vos résultats grâce à l'égalité euclidienne. Prêt à devenir un as du partage ? C'est parti !
Qu’est-ce qu’une division euclidienne ?
Avant de se lancer dans les calculs, il est impératif de bien définir ce qu'est cette opération et de maîtriser le vocabulaire précis qui l'accompagne.
Division euclidienne : définition
La division euclidienne (ou division entière) est une opération qui associe deux entiers naturels (le dividende et le diviseur) à deux autres entiers uniques : le quotient et le reste.
Contrairement à la division décimale, on ne cherche pas à aller "après la virgule". On s'arrête dès qu'on ne peut plus faire de paquets entiers avec le diviseur.
Dans une division euclidienne, le reste doit toujours être strictement plus petit que le diviseur. Si votre reste est plus grand, c'est que vous n'avez pas fini le partage !
Vocabulaire associé à la division euclidienne
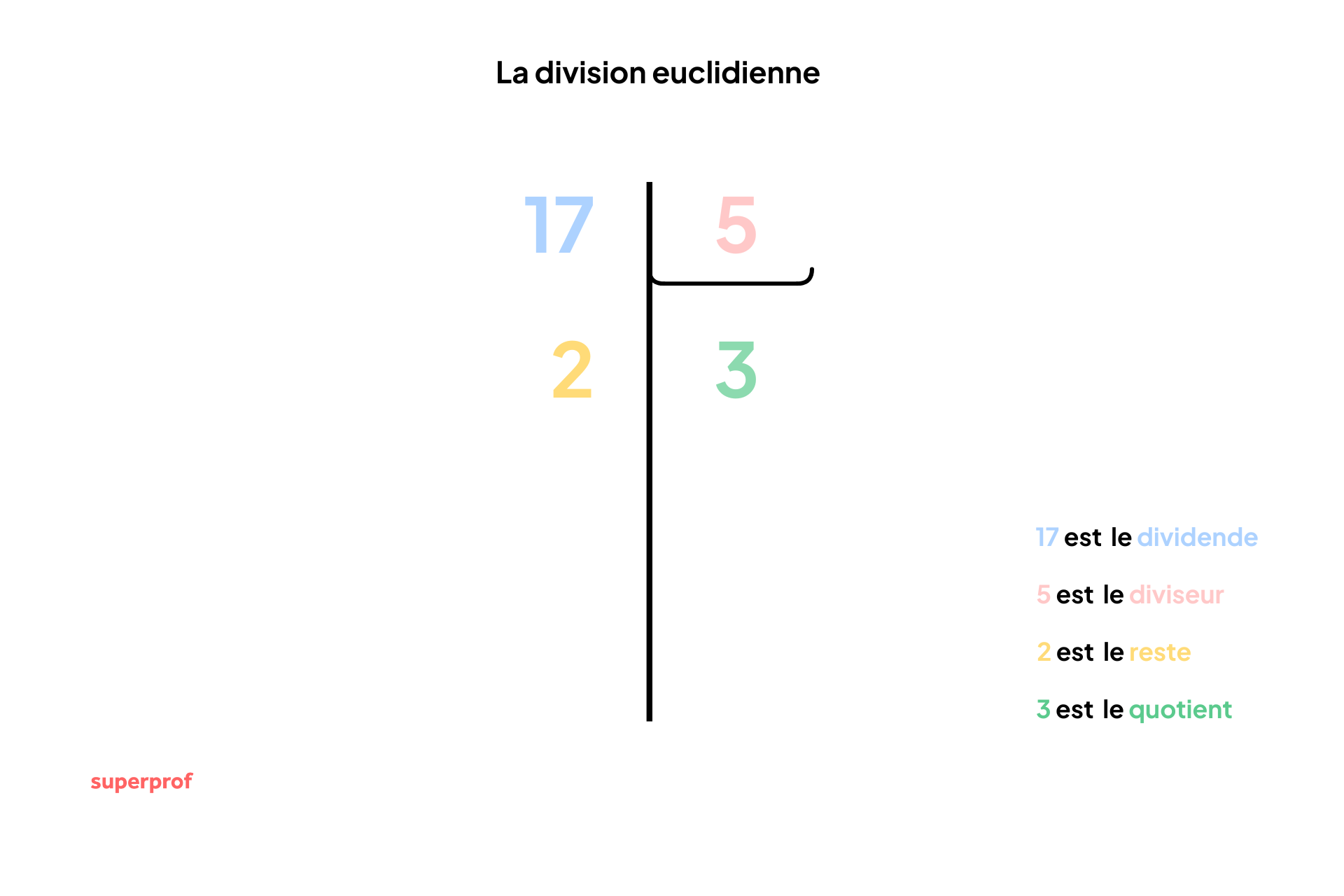
Pour ne plus jamais confondre les termes, voici les définitions exactes des quatre acteurs de cette opération. Imaginons l'opération : 17 ÷ 5.
- Le Dividende (D) : C'est le nombre total que l'on souhaite diviser. Dans notre exemple, c'est 17. C'est la quantité "à partager".
- Le Diviseur (d) : C'est le nombre par lequel on divise. Dans notre exemple, c'est 5. Cela représente la taille des paquets ou le nombre de personnes.
- Le Quotient (q) : C'est le résultat division euclidienne (la partie entière). Dans notre exemple, c'est 3 (car dans 17, on peut mettre 3 fois 5).
- Le Reste (r) : C'est ce qu'il "reste" à la fin du partage car ce n'est pas assez grand pour faire un nouveau paquet. Dans notre exemple, c'est 2 (car
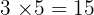, et pour aller à 17, il manque 2).
Comment faire une division euclidienne ?
Vous vous demandez comment faire une division euclidienne sans erreur ? Que ce soit de tête pour des petits nombres ou posée sur une feuille pour des grands nombres, la logique est la même. Décomposons la méthode.
Étape 1 : Identifier le dividende et le diviseur
C'est la base. Si vous avez un énoncé du type "On répartit 150 élèves dans des bus de 40 places", posez-vous la question :
- Qu'est-ce que je partage ? Les 150 élèves. C'est le Dividende.
- Par combien je divise ? Par paquets de 40. C'est le Diviseur.
Étape 2 : Trouver le plus grand multiple (Calcul du quotient)
C'est ici que la connaissance de vos [tables de multiplication] est cruciale. Vous devez trouver combien de fois le diviseur rentre "entièrement" dans le dividende, sans le dépasser.
Prenons l'exemple :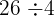 
.
On cherche dans la table de 4 :
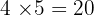(Trop petit)
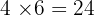(On s'approche)
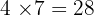(Trop grand ! On a dépassé 26).
Le bon multiplicateur est donc 6.
Le quotient est 6.
Étape 3 : Calculer le reste
Une fois le quotient trouvé, il suffit de calculer ce qu'il reste.
Calculons la différence entre le dividende et le produit que nous venons de trouver.
- On a utilisé .
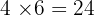- On avait 26 au départ.
- Reste =
.
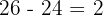Le reste est 2.
La méthode de la division posée (La potence)
Pour des grands nombres, le calcul mental ne suffit plus. Il faut poser la division. Prenons un division euclidienne exercice corrigé détaillé :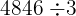 
.
On commence par la gauche : On regarde le chiffre des milliers du dividende (4). Est-ce que je peux diviser 4 par 3 ? Oui.
- Dans 4, il y a 1 fois 3.
- J'écris 1 au quotient.
- 1 x 3 = 3.
- 4 - 3 = 1. Il reste 1.
On descend le chiffre suivant : On abaisse le 3 à côté du 1. Cela forme le nombre 13.
- Dans 13, combien de fois 3 ?
- 3 x 4 = 12. C'est le plus proche.
- J'écris 4 au quotient.
- 13 - 12 = 1. Il reste 1.
On descend le chiffre suivant : On abaisse le 4 à côté du 1. Cela forme le nombre 14.
- Dans 14, combien de fois 3 ?
- 3 x 4 = 12. C'est le plus proche.
- J'écris 4 au quotient.
- 14 - 12 = 1. Il reste 2.
On descend le dernier chiffre : On abaisse le 6 à côté du 2. Cela forme le nombre 26.
- Dans 26, combien de fois 3 ?
- 8 x 3 = 24 (car 9 x 3 = 27, c'est trop).
- J'écris 8 au quotient.
- 26 - 24 = 2. Il reste 2.
Résultat :
- Le quotient division euclidienne est 1448.
- Le reste est 2.
- On vérifie que le reste (2) est bien inférieur au diviseur (3). C'est bon !
L'égalité euclidienne : la formule magique pour vérifier
Une fois le calcul terminé, comment être sûr de ne pas s'être trompé ? Il existe une formule infaillible appelée égalité euclidienne ou preuve de la division.
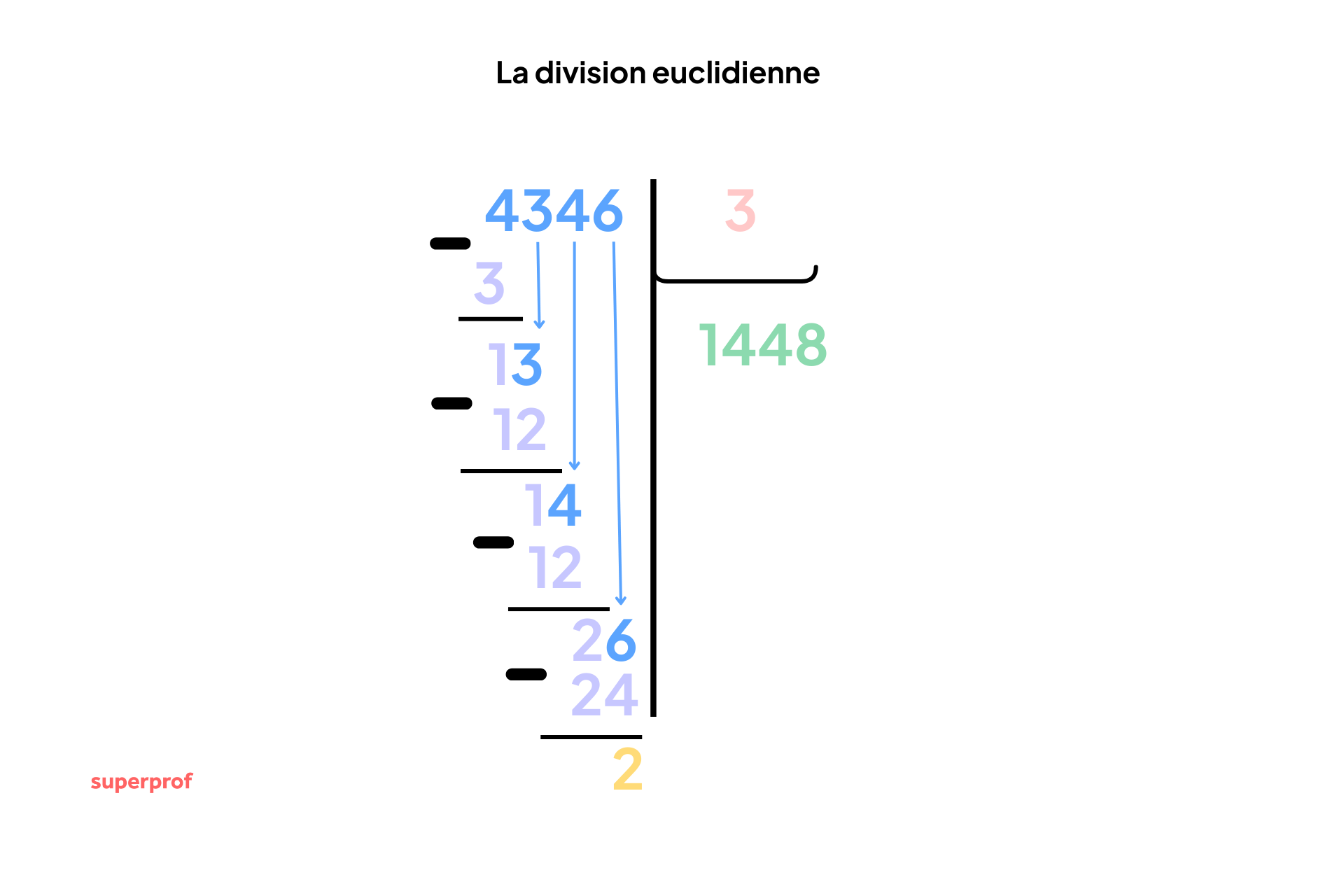
Division euclidienne formule
La relation qui lie les quatre nombres est la suivante :
Avec une condition obligatoire : 0 ≤ Reste < Diviseur.
Exemple de vérification
Reprenons notre calcul précédent : 4346/3. Nous avions trouvé un quotient de 1448 et un reste de 2.
Appliquons la formule :
- Calculons 1448 x 3 + 2.
- 1448 x 3 = 4344.
- 4344 + 2 = 4346.
On retrouve bien le dividende de départ ! Le calcul est exact.
Cette méthode de vérification fonctionne aussi si vous effectuez une division avec des nombres décimaux, comme mentionné dans d'anciennes versions de cours.
Par exemple, pour 14,9 divisé par 7 :
Si on dit que cela fait 2,1 et qu'il reste 0,2.
On vérifie :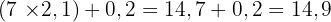 
.
Cependant, en mathématiques pures, la "division euclidienne" ne concerne traditionnellement que les nombres entiers.
Mais comment faire si le nombre à partager possède une virgule (comme une somme d'argent) ? Découvrez la méthode pas à pas dans notre cours sur la division d'un nombre décimal par un nombre entier.
Propriétés et applications de la division euclidienne
Pourquoi apprendre cela ? Est-ce juste pour embêter les élèves ? Pas du tout ! Cette opération possède des propriétés uniques qui servent de socle à de nombreuses logiques mathématiques.
Propriétés fondamentales
Unicité : Pour un couple de nombres donné (dividende et diviseur), il n'existe qu'un seul couple (quotient et reste) possible. Vous ne pouvez pas trouver un autre résultat si vous avez respecté les règles.
La contrainte du reste : On insiste, mais c'est vital : le reste est toujours strictement inférieur au diviseur. Si vous trouvez un reste de 6 en divisant par 5, c'est que vous pouviez faire un paquet de plus !
Domaine d'application : Elle s'applique aux entiers naturels (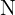
) et peut s'étendre aux entiers relatifs (
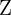), mais ne s'utilise pas telle quelle avec les nombres réels (
).
Où utilise-t-on la division euclidienne ?
Au-delà de la salle de classe, voici où ce concept est roi :
- La conversion du temps : Si vous avez 135 minutes et que vous voulez savoir combien cela fait d'heures.
- 135 / 60 (car 60 min dans une heure).
- Quotient = 2, Reste = 15.
- Résultat : 2 heures et 15 minutes. C'est une division euclidienne !
- La divisibilité : Si le reste est nul (r=0), alors on dit que le dividende est un multiple du diviseur, ou qu'il est divisible par lui.
- Exemple : 12 / 4. Quotient = 3, Reste = 0. Donc 12 est divisible par 4.
- Le calcul du PGCD : L'algorithme d'Euclide, qui permet de trouver le Plus Grand Commun Diviseur entre deux nombres (très utile pour simplifier des fractions), n'est qu'une succession de divisions euclidiennes.
- L'informatique et la cryptographie : En programmation, l'opérateur "modulo" (souvent noté
%) renvoie le reste de la division euclidienne. C'est utilisé pour savoir si un nombre est pair (reste de la division par 2 = 0) ou pour chiffrer des messages secrets (arithmétique modulaire).
Exercices pratiques sur la division euclidienne
Pour maîtriser le résultat division et la méthode, rien ne vaut l'entraînement. Voici quelques exercices progressifs.
Exercice 1 : Calcul mental et vocabulaire
Complétez les phrases suivantes en trouvant le quotient et le reste :
Dans la division euclidienne de 23 par 5, le quotient est ... et le reste est ...
Ce champ est requis.
Dans la division euclidienne de 40 par 6, le quotient est ... et le reste est ...
Ce champ est requis.
L'égalité euclidienne s'écrit : 50 = 7 x ... + ...
Ce champ est requis.
Exercice 2 : Problème concret
Un fleuriste reçoit 150 roses. Il veut composer des bouquets de 12 roses chacun.
Combien de bouquets entiers peut-il réaliser ?
Combien de roses lui restera-t-il ?
Ce champ est requis.
Il faut effectuer la division euclidienne de 150 par 12.
12 x 10 = 120
12 x 12 = 144
150 - 144 = 6
Il peut réaliser 12 bouquets.
Il lui restera 6 roses non utilisées.
Exercice 3 : Retrouver le dividende
Je suis un nombre entier. Si on me divise par 9, le quotient est 8 et le reste est 5. Qui suis-je ?
Ce champ est requis.
Utilisons la division euclidienne formule : D = x q + r.
Ici :
d = 9
q = 8
r = 5
Calcul : D = (9 x 8) + 5 = 72 + 5 = 77.
Le nombre cherché est 77.
Flashcards : Vrai ou Faux ?
Testez vos connaissances sur la division euclidienne ! C'est l'heure du bilan ! Tu connais la réponse ? Clique sur ✅. Sinon, clique sur ❌. N'oublie pas de retourner la carte pour voir la solution !
La théorie est acquise ? Passez maintenant à la pratique pour consolider vos connaissances grâce à notre fiche exercice : divisibilité et division euclidienne.
Nous espérons que cet article vous a permis de démystifier la division euclidienne.
Vous avez aimé cet article ? Notez-le !
Loading...
Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Sa n’a pas fonctionné 😡
Bonjour ! Je vous invite à découvrir nos formateurs passionnés sur Superprof, toujours prêts à vous offrir un accompagnement adapté à vos besoins. Que votre journée soit aussi enrichissante et agréable que possible ! :)
C’est bien bon
J’aime trop l’application de Olivier
Je vais vérifier le résultat parce que j’avais joué mais je n’arrive pas
D=d x (q+r). me semble suspect
Ce n’est pas suspect mais erroné. L’équation correct est D = d x q + r. Avec les parenthèse le reste est aussi pris dans la multiplicatio ce qui fausse le résultat. .
1249:5
oui , ça devrait être D = (d x q) + r , non ?