Chapitres
Les ensembles de nombres forment la base de toutes les mathématiques. Ils permettent de classer les nombres selon leurs propriétés et leur comportement, et sont essentiels pour progresser dans des notions comme l’algèbre, l’analyse, la logique ou encore la physique.
Dans cet article, nous allons explorer, étape par étape, tous les ensembles de nombres que vous rencontrerez, des plus simples aux plus complexes.

Les ensembles de nombres : classification complète
| Ensemble | Symbole | Description | Exemples |
|---|---|---|---|
| Nombres naturels | ℕ | Nombres positifs entiers | 0,1,2,3,10,1500 |
| Nombres entiers | ℤ | Nombres entiers positifs et négatifs | -5,-1,0,1,12,500 |
| Nombres rationnels | ℚ | Nombres positifs et négatifs sous forme de fraction | 1/2 , -3,5 , 0,3333... |
| Nombres irrationnels | ℝ \ ℚ | Nombres à décimales infinies sans répétition qui ne sont pas des fractions | π, √2, e |
| Nombres réels | ℝ | Tous les nombres possibles représentés sur une droite contenue | -1, 0, π, 3/4 |
| Nombres complexes | ℂ | Nombres avec une partie imaginaire 𝑖 | 2 + 3𝑖, -𝑖 |
Les nombres naturels (ℕ)
Les nombres naturels sont l'ensemble le plus intuitif des mathématiques. Ils sont apparus pour quantifier les choses. Un nombre naturel est un nombre positif compris entre 0 et l'infini. Ils sont représentés par l'ensemble ℕ.
Ces nombres sont principalement utilisés pour dénombrer et ordonner. Ce sont ceux que l'on rencontre le plus fréquemment dans la vie quotidienne. On les utilise pour donner le classement d'un concours, son âge ou encore un numéro de téléphone.
Certaines opérations mathématiques sont toujours possibles dans ℕ. C'est le cas de l'addition et de la multiplication. Leur résultat est toujours un entier naturel.
En ce qui concerne la division et la soustraction, seulement certaines seront possibles, en fonction des nombres utilisés.
Les nombres entiers (ℤ)
Les nombres entiers sont une version améliorée des nombres naturels. En effet, l'ensemble ℤ contient tous les nombres de l'ensemble ℕ en y ajoutant leurs opposés : les nombres négatifs.
On les a inventés afin de pouvoir effectuer toutes les soustractions. Si par exemple 5 - 8 était impossible dans ℕ, il y a maintenant une solution dans ℤ : -3.
Pour les opérations d'addition et de multiplication, pas de problème, elles sont toutes possibles dans ℤ lorsqu'on utilise des entiers. Attention cependant, toutes les divisions ne sont pas possibles dans ℤ, notamment si le résultat ne donne pas un entier.
Les nombres entiers sont aussi présents au quotidien, ce sont ceux que l'on utilise pour donner la température ou encore pour les finances (solde d'un compte bancaire). L'altitude et le niveau d'un ascenseur seront eux aussi des entiers.
ℤ ne vient pas remplacer ℕ mais au contraire, il le contient. On dit que ℕ est inclus dans ℤ et cela se note ℕ ⊂ ℤ.
Les nombres rationnels (ℚ)
Les nombres rationnels forment l'ensemble ℚ. Ils servent à représenter les fractions. En effet, que ce soit avec les nombres naturels ou entiers, lorsque l'on essaie de diviser un nombre par un plus grand que lui alors aucune solution n'existe. Grâce aux nombres rationnels, tous les nombres peuvent s'écrire sous la forme a / b.
Cette nouvelle notation permet en plus d'exprimer les nombres à virgule finis (tels que 0,5) mais aussi les nombres à virgule infinis mais périodiques comme 1 / 3 (0,333...).
Contrairement aux nombres naturels et entiers, les nombres rationnels sont très denses si on les représente sur une droite numérique. Par exemple, dans ℕ et ℤ, il n'y a rien entre 3 et 4. Pourtant, dans ℚ, il existe une infinité de nombres entre 3 et 4.
Dans les usages quotidiens, on retrouve les nombres rationnels dans diverses conditions, comme les pourcentages ou encore les probabilités.

Pour faire le lien avec les deux parties précédentes, voici comment les ensembles sont inclus les uns dans les autres :
ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ
Les nombres irrationnels
Les nombres irrationnels sont une catégorie un peu à part des mathématiques. Leur découverte a un peu bouleversé les mathématiciens grecs qui pensaient que tous les nombres pouvaient s'écrire sous la forme de fractions. Dans la réalité, une multitude de nombres ne peuvent pas s'écrire sous forme fractionnaire, c'est ce que l'on appelle des nombres irrationnels. On y retrouve par exemple les nombres infinis à virgule non périodiques.
En voici quelques exemples : π, e ou encore √2.
Les nombres réels (ℝ)
Les nombres réels sont le dernier niveau des ensembles de nombres. Ils contiennent absolument tous les nombres en allant de l'infini négatif au positif en passant par 0, incluant même ceux avec une infinité de chiffres après la virgule sans logique. Ils sont regroupés dans l'ensemble ℝ qui contient tous les ensembles ℕ, ℤ et ℚ.
Sur une droite géométrique, tous les points peuvent correspondre à un nombre réel.
Les applications ne manquent pas pour les nombres réels. Ils sont utilisés pour donner des mesures (angles, aires, volumes et longueurs) en géométrie, pour effectuer des calculs en mathématiques (dérivées, intégrales ou encore limites) mais aussi pour modéliser un nombre important de grandeurs en physique (les vitesses, les masses, les distances).

L'ensemble des réels ℝ est composé des nombres irrationnels et des rationnels ℚ
Les nombres complexes (ℂ)
Les nombres complexes sont apparus afin de régler un problème des mathématiques : les équations impossibles ! C'est le cas par exemple de l'équation x² + 1 = 0, qui donne comme solution que x² = -1, ce qui est impossible dans ℝ.
Ils reposent sur l'existence du nombre 𝑖 qui se définit par la relation 𝑖 ² = - 1. Les nombres complexes sont regroupés eux aussi dans un ensemble qui se nomme ℂ.
La forme d'un nombre complexe est : 𝑧 = a + b𝑖. On dit que a est la partie réelle et b la partie imaginaire.
Leur représentation graphique ne se fait plus sur une droite mais sur un plan, que l'on appelle le plan complexe. Dans ce plan, L'axe des abscisses représente la partie réelle et l'axe des ordonnées représente la partie imaginaire.
Même si leur existence contredit de nombreuses règles mathématiques, ils sont maintenant devenus des outils indispensables. Tout d'abord en mathématiques en permettant de trouver des solutions aux équations habituellement impossibles. Ensuite, les nombres complexes sont aussi fréquemment rencontrés en physique, notamment en électricité pour les calculs de courant alternatif ou encore en traitement des ondes radio, audio et enfin en mécanique quantique pour les calculs sur la physique des particules.
Comment les ensembles de nombre en maths s’emboîtent-ils ?
Schéma d’inclusion des ensembles mathématiques
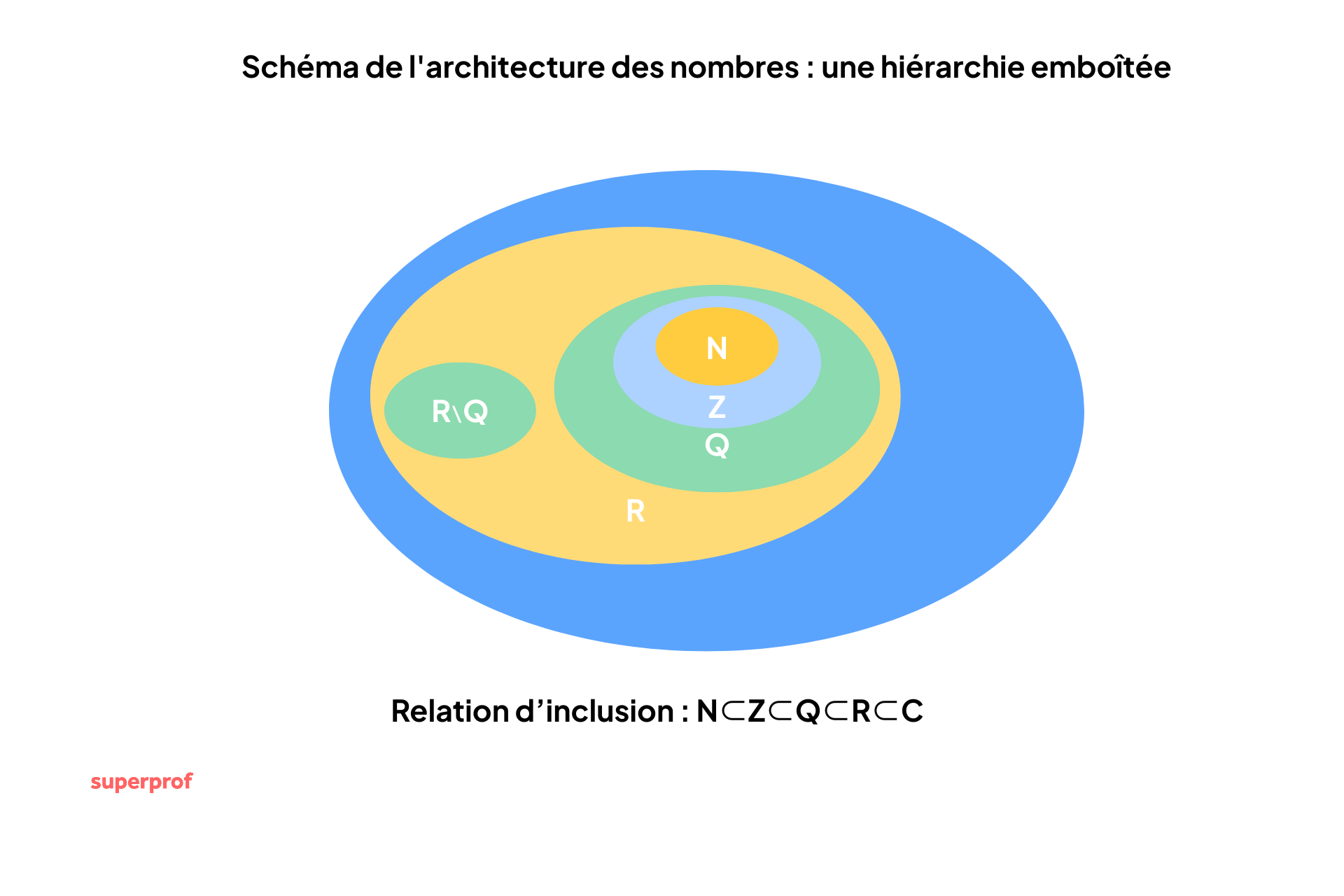
Comprendre les relations entre ensembles
Pour mieux comprendre les relations entre les différents ensembles, voici un tableau qui explique comment chaque ensemble répond à un problème posé par le précédent :
| Ensemble existant | Le problème bloquant | La solution |
|---|---|---|
| ℕ | Certaines soustractions sont impossibles | Création de ℤ (nombres entiers) |
| ℤ | Certaines divisions sont impossibles | Création de ℚ (nombres rationnels) |
| ℚ | Certaines solutions n'existent pas (√2 par exemple) | Création de ℝ (nombres réels) |
| ℝ | Certaines équations n'ont pas de solution (x² = -1) | Création de ℂ (nombres complexes) |
Pour signifier l'appartenance ou non à un ensemble, il existe des symboles mathématiques :
- Le symbole "appartient" : ∈
- Le symbole "n'appartient pas" : ∉
Par exemple, on peut dire que 6 ∈ ℕ mais - 6 ∉ ℕ.
Attention à ne pas commettre certaines erreurs : il existe de "fausses" fractions ou racines.
Par exemple, 10 / 2 semble être un nombre rationnel mais en réalité 10 /2 = 5, ce qui est un nombre naturel. Même problème pour √25, on pourrait croire qu'il est irrationnel ou réel alors que √25 = 5, ce qui est aussi un nombre de ℕ !
Attention également aux nombres à virgules inutiles tels que 5,0 qui appartient bien à ℕ et n'est pas forcément un rationnel car il y a une virgule.
Comment représenter un ensemble de nombres ?
Notation en extension
Voici les différents symboles utilisés pour représenter la notation des ensembles de nombres :
| Symbole | Nom | Rôle | Exemple |
|---|---|---|---|
| { } | Les accolades | Elles servent à délimiter le début et la fin d'une liste | A = {2,4,6} |
| , ou ; | La virgule ou le point-virgule | Ils séparent les différents éléments d'une liste | B = {1,5,12} |
| ... | Les points de suspension | Ils indiquent que la liste continue en suivant la même logique, souvent jusqu'à l'infini | ℕ = {0,1,2,3,…} |
| ∅ | L'ensemble vide | Il s'agit d'un ensemble sans rien à l'intérieur | Ensemble des carrés ronds = ∅ |
Notation en compréhension
Quand un ensemble est trop grand ou trop compliqué pour le lister, on le définit par une propriété commune à tous ses éléments.
Voici un exemple parlant : ℕ = { x ∈ ℤ ∣ x ≥ 0 } se lit "L'ensemble des x appartenant aux entiers (Z) tels que (∣) x est supérieur ou égal à 0".
Voici un tableau qui reprend tous les symboles ainsi que la façon dont ils se lisent :
| Symbole | Se lit | Rôle |
|---|---|---|
| {x…} | "L'ensemble des x..." | La variable : élément générique que l'on veut définir |
| ∈ E | "...appartenant à l'ensemble E..." | L'univers : on précise dans quel ensemble on cherche |
| ∣ (ou :) | "...tels que..." | La frontière : elle sert de séparation entre la variable et sa condition |
| Condition | "...qui vérifient la règle." | Le filtre : définit la propriété mathématique que les nombres doivent respecter |
Représentation sur la droite numérique
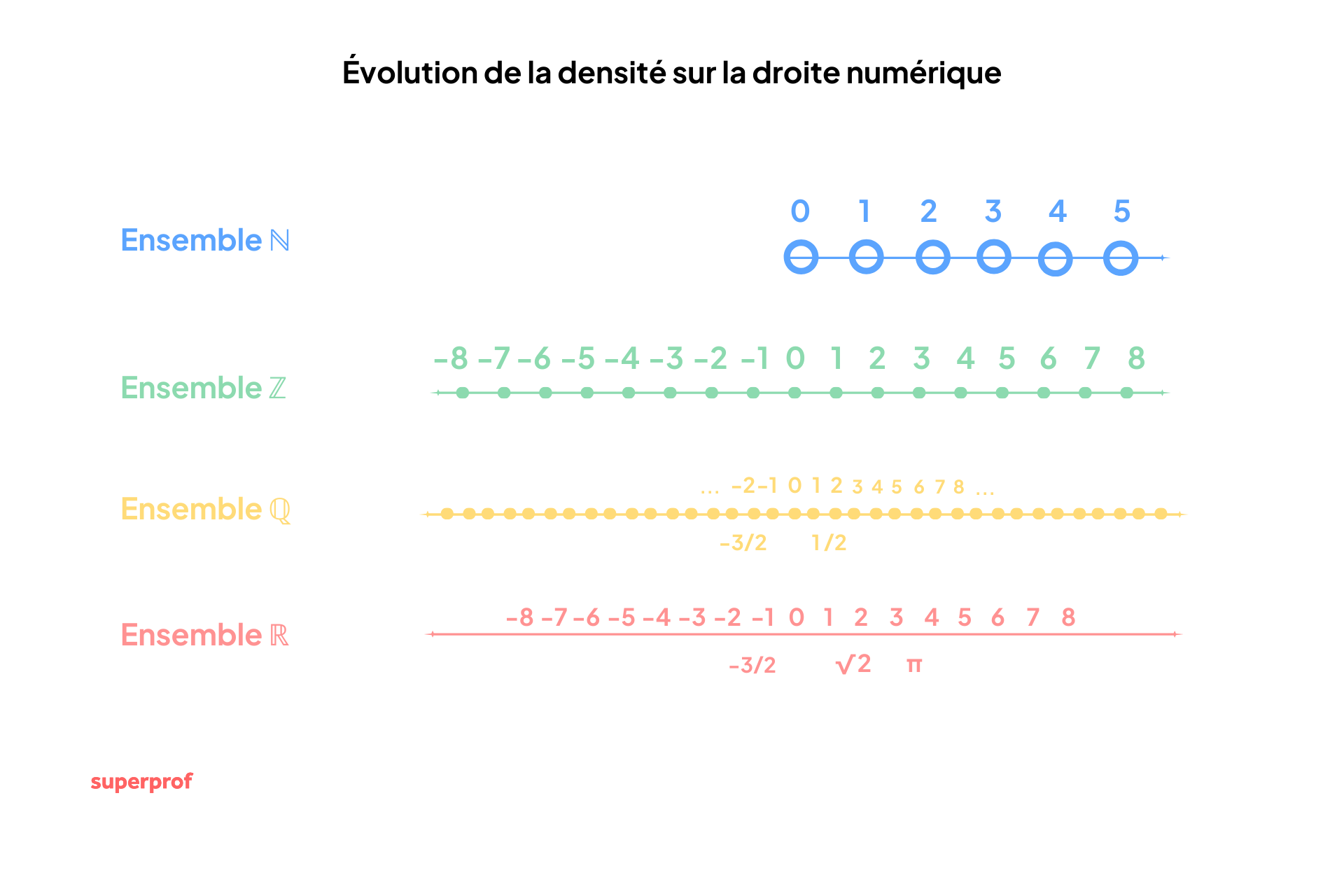
Chacun des ensembles est de plus en plus précis, avec de plus en plus de nombres contenus.
Où utilise-t-on les ensembles de nombres ?
En mathématiques pures
Dans les mathématiques pures, les ensembles de nombre ne servent pas qu'à classer les nombres. Ils permettent aussi de définir un certain nombre de règles de calcul et de résolution d'équations. Sans savoir dans quel ensemble on travaille, il est souvent presque impossible de résoudre le problème.
L'une des branches des mathématiques est l'arithmétique, l'étude des nombres entiers. Il s'agit de la branche la plus ancienne des mathématiques.
On y travaille donc exclusivement sur ℕ et ℤ. Ces sont ces études qui ont mené à la compréhension des nombres premiers, du calcul de PGCD (plus grand commun diviseur) et de la divisibilité.
Encore aujourd'hui, l'arithmétique reste un élément incontournable de la cryptographie que l'on retrouve dans les cartes bancaires ou les cartes vitales par exemple.

Dans l'étude des fonctions, de leurs variations et des limites, on se rapporte à une autre branche : l'analyse.
Ces études se déroulent principalement dans ℝ et permettent les calculs sur les dérivées, les intégrales ou encore les limites.
Pour finir, l'ensemble ℝ est primordial pour permettre de tracer des courbes lisses sans interruption pour représenter des fonctions.
Enfin, pour faire des démonstrations en mathématiques, on commence régulièrement par une phrase du genre "Soit x, appartenant à l'ensemble...". Le choix de l'ensemble change profondément les calculs et les solutions possibles.
Par exemple, résoudre l'équation x² = 2 est impossible dans ℚ alors que dans ℝ il y a deux solutions : √2 et - √2.
Les ensembles de nombres sont aussi fortement utilisés dans de nombreux théorèmes. Voici un tableau qui en récapitule certains :
| Théorème | Ensemble mis en cause | Définition |
|---|---|---|
| Dernier théorème de Fermat | ℕ et ℤ | Il stipule qu'il n'y a pas de solutions entières à an + bn = cn pour n > 2. |
| Théorème des valeurs intermédiaires | ℝ | Il garantit qu'une fonction continue passe par toutes les valeurs. Cela ne fonctionne que parce que ℝ est complet. |
| Théorème fondamental de l'algèbre | ℂ | Il affirme que tout polynôme a une racine. Ce n'est vrai que si on accepte les nombres complexes. |
En sciences appliquées
Les mathématiciens créent les outils mais ce sont souvent les physiciens, les ingénieurs et les informaticiens qui les utilisent.
Les nombres complexes sont très utilisés en physique car ils permettent de décrire des phénomènes d'oscillation. C'est le cas par exemple de l'électrotechnique qui analyse le courant alternatif. Pour calculer la tension et le courant, les nombres complexes sont souvent utilisés. Prenez la formule de calcul de l'impédance : Z = R + 𝑖 X qui met en évidence 𝑖.
En physique quantique aussi, le nombre 𝑖 est utilisé dans l'équation de Schrödinger, qui sert à décrire le comportement de l'atome à l'échelle de l'infiniment petit.
Passons maintenant aux nombres réels de ℝ. C'est l'ensemble de prédilection de la physique de base. Que ce soit le temps, la vitesse, la distance, la température ou la masse, toutes ces données sont modélisées par des nombres naturels. Les équations différentielles sont toujours résolues sur ℝ pour répondre à des problèmes de simulation de la réalité.
Enfin, voyons à quoi servent les ensembles des nombres naturels et entiers en sciences appliquées, malgré leur simplicité apparente. L'une des applications clé est l'informatique. En effet, pour un ordinateur, même le plus complexe des calculs n'est qu'une suite de 1 et de 0. Pour faire des algorithmes et du classement, ce sont encore les nombres de ℕ qui sont utilisés.
De même, pour stocker de grands nombres, l'ordinateur utilisera des nombres rationnels. Prenons pi par exemple, l'ordinateur ne pourra pas stocker π en un seul morceau, mais plutôt sous forme de nombre à virgule flottante, qui est en réalité une fraction. Pour faire simple, tout réel est approximé par un rationnel en informatique.
Ensemble de nombre : exercices pratiques
Afin de s'entraîner sur les ensembles de nombres et ne pas les confondre, voici quelques exercices corrigés.
Consigne : Pour chaque nombre, indiquez le plus petit ensemble auquel il appartient parmi ℕ, ℤ, ℚ et ℝ.
- - 5
- 10,5
- √4
- 1 /3
- π
- -12 / 4
- −5 : C'est un entier négatif. → ℤ
- 10,5 : C'est un nombre à virgule finie (décimal). → ℚ
- √4 : Attention au piège ! √4 =2. C'est un entier positif. → ℕ
- 1 / 3 : C'est une fraction irréductible (0,333...). → ℚ
- π : C'est un nombre avec des décimales infinies sans suite logique. → ℝ (nombre irrationnel)
- -12 / 4 : On simplifie la fraction : −12÷4=−3. C'est un entier négatif. → ℤ
Consigne : Dites si les affirmations suivantes sont vraies ou fausses. Justifiez brièvement.
- Tous les nombres entiers sont des nombres réels.
- Le nombre −2,5 appartient à ℤ.
- L'équation x² = 2 a une solution dans ℚ.
- ℕ⊂ℤ.
- VRAI. L'ensemble ℤ est inclus dans R (ℤ⊂ℝ). Tout entier est aussi un réel.
- FAUX. L'ensemble ℤ ne contient pas de nombres à virgule. −2,5 appartient à ℚ.
- FAUX. La solution est √2 (et -√2 ), qui est un nombre irrationnel. Il n'existe pas de fraction égale à √2 . La solution est dans ℝ.
- VRAI. L'ensemble des nombres naturels (0, 1, 2...) est "contenu" dans l'ensemble des entiers relatifs.
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
« R » pour réels OK mais « IR » pour « ? »… Quand dans un ouvrage, on parle de « R » et « IR », quelle est la différence entre « R » et « IR »?…
Bonjour, « R » et « IR » désignent le même ensemble : celui des nombres réels. La lettre « I » signifie simplement « ensemble » dans certaines notations francophones (comme IN pour les naturels, IZ pour les entiers, etc.). Il n’y a donc pas de différence entre les deux, il s’agit juste d’une question de notation selon les ouvrages. Belle journée à vous :)
Écrire l’intervalle correspondante R+ , R-, , R plus moins , R moins plus
Merci c’est facile à comprendre👏👊
bon travail, merci beaucoup
merci rdm
Good Job ! ;-)