Chapitres
La fonction affine est l'une des fonctions les plus simples mais aussi les plus utiles en mathématiques. Il s'agit du premier outil de modélisation.
On la retrouve dans de nombreux concepts de la vie quotidienne. C'est le cas par exemple d'une tirelire dans laquelle on ajoute 5 € toutes les semaines ou encore d'un abonnement prix fixe + consommation.
f(x) = a x + b
Dans cet article, nous allons décortiquer cette fonction et ainsi vous aider à la maîtriser complètement. Nous passerons en revue la définition, les propriétés mais aussi sa représentation graphique. Pour finir, vous pourrez effectuer quelques exercices d'entraînement.
Qu’est-ce qu’une fonction affine ?
Définition d’une fonction affine
D'un point de vue mathématique, les fonctions affines sont définies sur l'ensemble des nombres réels (ℝ).
Comme vu précédemment, la fonction affine se note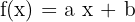 
. a et b sont des constantes mais x est une variable. Pour chaque x il existe une image que l'on note f(x).
Les constantes a et b portent elles aussi des noms particuliers : a est le coefficient directeur et b est l'ordonnée à l'origine.
Par exemple, dans la fonction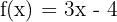 
, a = 3 et b = - 4.
Il existe deux cas particuliers des fonctions affines. Cela arrive quand l'une des deux constantes est nulle. Deux sous-catégories naissent alors : les fonctions linéaires et les fonctions constantes.
Les fonctions linéaires sont des fonctions affines dans lesquelles b = 0. Leur formule est donc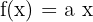 
. C'est une simple fonction de proportionnalité.
Les fonctions constantes ont la particularité que a = 0. Cela fait disparaître le terme en x, donnant comme formule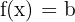 
. Dans ce cas, peu importe la valeur de x, le résultat sera toujours b. Sur le graphique, cela se traduit par une droite horizontale, parallèle à l'axe des abscisses.
Propriétés d’une fonction affine
La fonction affine possède différentes propriétés définies par les constantes a et b.
Tout d'abord, le sens de variation. Il définit si une fonction est croissante ou décroissante. Pour que f soit croissante, il faut que a soit supérieur à 0 et pour que f soit décroissante, il faut que a soit inférieur à 0.
Ce tableau récapitule les propriétés de la fonction affine selon son coefficient directeur :
| Propriété | Conséquence |
|---|---|
| Sens de variation | Si a < 0 : décroissant Si a > 0 : croissant |
| Ordonnée à l'origine | Coupe l'axe des abscisses en f(0) |
| Représentation graphique | Droite qui monte si croissante Droite qui descend si décroissante |
Voyons maintenant l'impact de l'ordonnée à l'origine, b. Cette constante porte bien son nom. En effet, si elle n'influence pas la direction de la fonction, elle influence sa hauteur sur la représentation graphique.
L'ordonnée à l'origine représente la valeur de f(x) quand x = 0. Sur le graphique, cela se traduit par l'emplacement où la droite de f(x) coupe l'axe des ordonnées.
Prenons la fonction f(x) = 2x + 3. Voici sa représentation graphique :
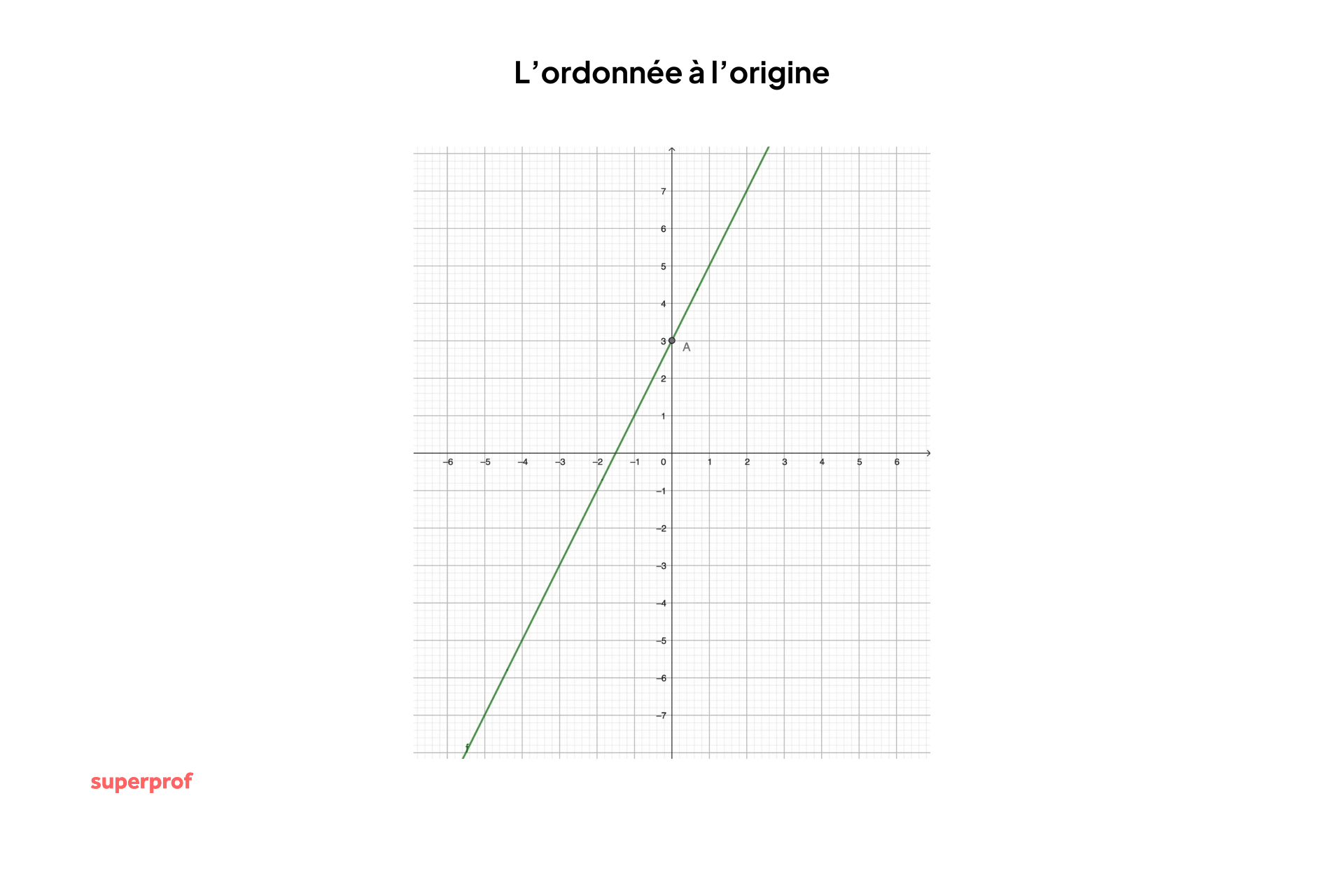
Ici a = 2 et b = 3. On distingue bien les points évoqués précédemment :
- a > 0 donc f(x) est croissante ;
- b = 3 donc f(0) = 3.
L'axe des ordonnées est donc bien coupé par la droite f(x) au point A, ordonnée à l'origine de coordonnées (0 ; 3).
Comment représenter une fonction affine ?
Pour représenter une fonction affine, on utilisera toujours une droite. Une règle simple de géométrie nous dit qu'il suffit de deux points pour tracer une droite. C'est donc la méthode que nous allons utiliser pour représenter graphiquement une fonction affine.
Pour commencer, il faut calculer deux images de x. Choisissez celles que vous voulez (les plus simples de préférence) afin de faciliter les calculs. Vous pouvez aussi calculer f(0), cela vous donnera directement l'ordonnée à l'origine.
Ensuite, sur un repère orthonormé, placer les deux points comme ceci : A (x ; f(x)) et B (y ; f(y)). Avec une règle, reliez les deux points A et B et prolongez le trait de chaque côté. La droite est maintenant créée !
Voyons cela avec un exemple précis : la fonction affine f(x) = 3x -4.
Commençons par choisir deux points : on prendra x = 0 et x = 2. Calculons :
f(0) = 3(0) + (-4) = 0 - 4 = -4 et f(2) = 3(2) + (-4) = 6 - 4 = 2.
On obtient donc deux points : A (0 ; -4) et B (2 ; 2). Prenons un repère orthonormé, puis plaçons les deux points :
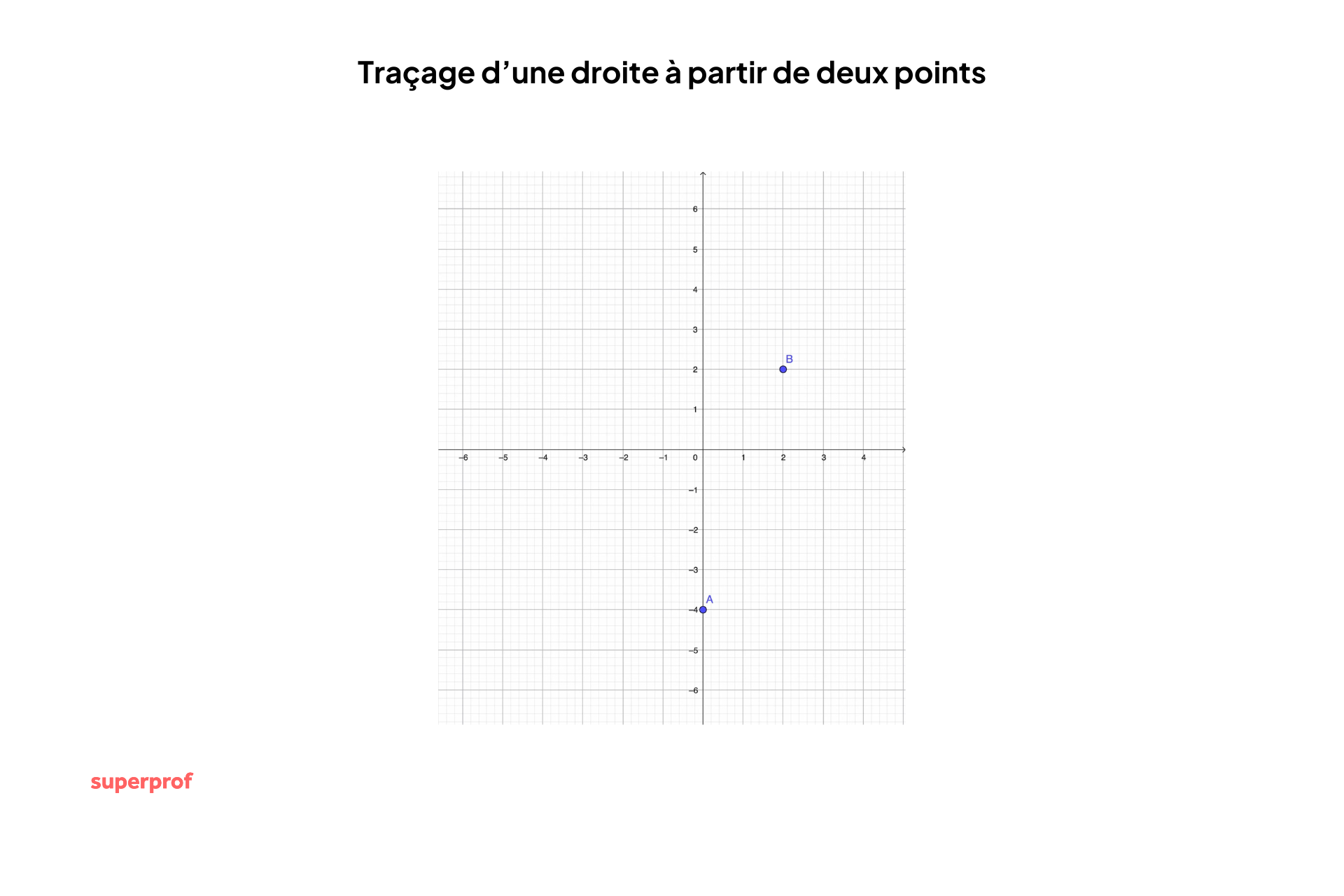
Ensuite, il suffit de relier les deux points tout en prolongeant le tracé au-delà de A et de B :
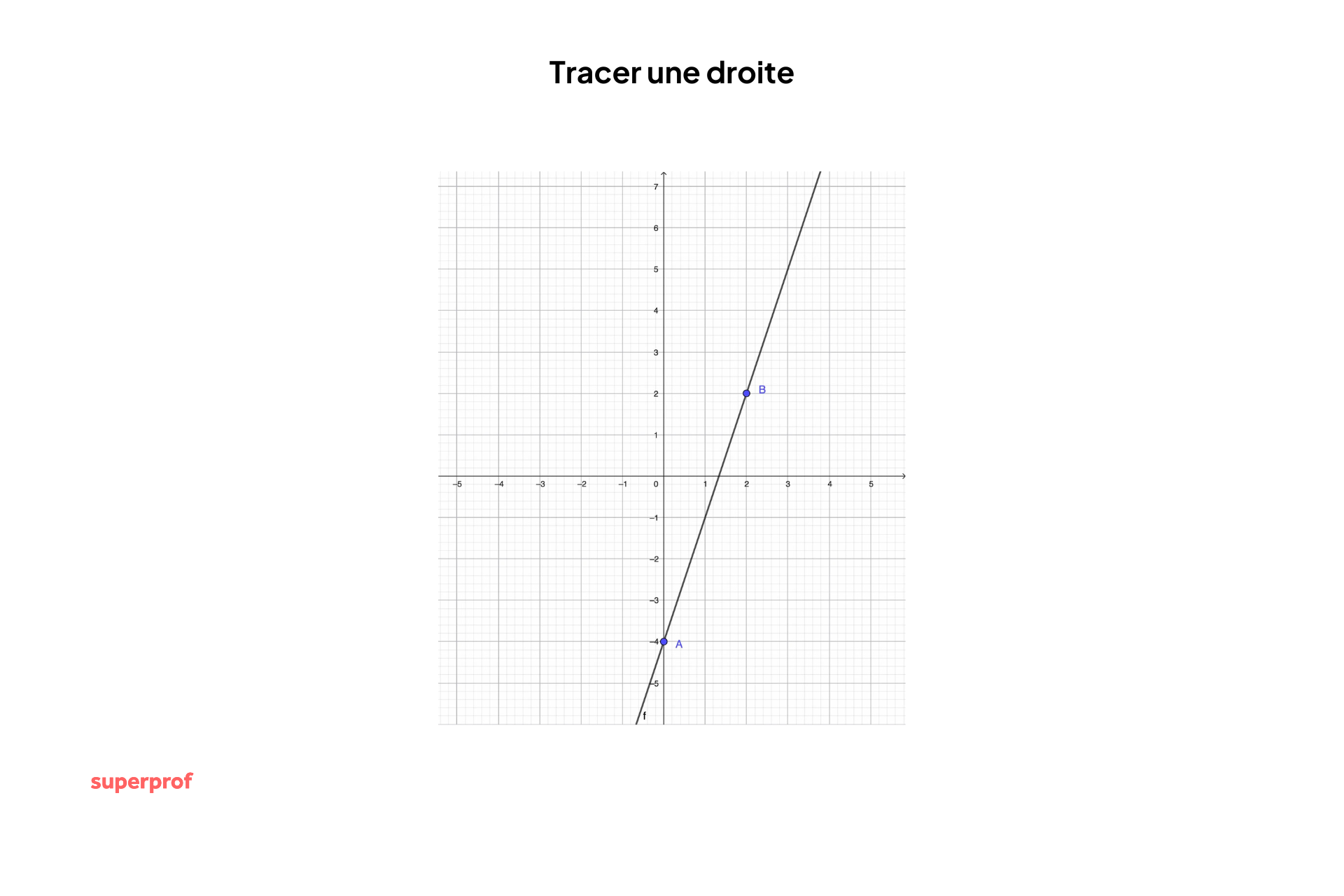
La droite représentant f(x) est maintenant tracée !
Afin de bien comprendre, voici un schéma reprenant toutes les propriétés et les caractéristiques de la fonction affine que l'on peut voir sur la représentation graphique :
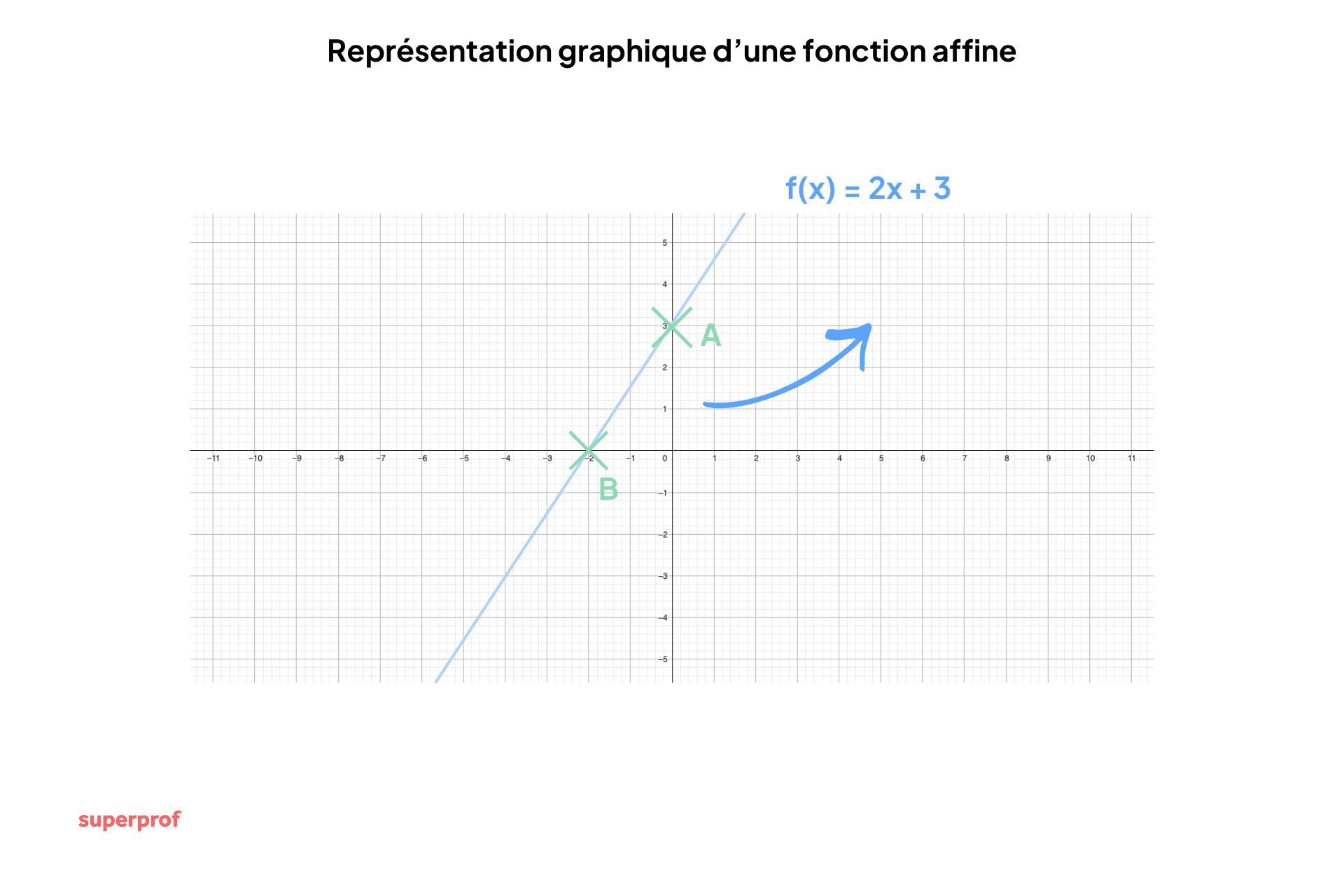
Comment retrouver la formule à partir de deux points ?
Imaginons que vous avez deux images d'une fonction mais pas sa formule. Comment retrouver la fonction et son expression ?
Prenons les images f(2) = 11 et f(4) = 17.
Commençons par calculer le coefficient directeur (a). Pour cela, il existe une formule pour deux points A(xA ; yA) et B(xB ; yB) :
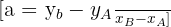
Dans notre cas, on a A (2 ; 11) et B (4 ; 17). Cela donne :
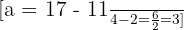
La fonction f(x) a donc 3 pour coefficient directeur. Elle est donc de la forme f(x) = 3x + b.
Il nous reste maintenant à trouver l'ordonnée à l'origine. Pour cela, prenons l'un des points précédents : A (2 ; 11) par exemple. Grâce à l'expression trouvée précédemment, cela donne une équation :
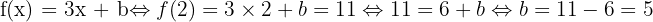
La fonction affine recherchée est donc f(x) = 3x + 5.
Utiliser le point d'intersection pour comparer deux offres
Prenons par exemple un cinéma. Il offre des places à 10 € pièce pour voir un film. Pour ceux qui s'abonnent avec une carte à 30 €, la place est à 5 €.
Si vous allez voir deux films, combien cela va vous coûter avec ou sans abonnement ?
Sans abonnement : 2 x 10 € = 20 €
Avec abonnement : 30 € + 2 x 5 € = 40 €
La formule sans abonnement est donc plus intéressante.
Mais si cette fois vous allez voir 10 films ?
Sans abonnement : 10 x 10 € = 100 €
Avec abonnement : 30 € + 10 x 5 € = 80 €
La formule avec abonnement est donc plus avantageuse.
Trouver ce "point d'équilibre" peut se faire par le calcul, grâce aux fonctions affines. Commençons par définir deux fonctions :
Formule sans abonnement : f(x) = 10x
Formule avec abonnement : g(x) = 5x + 30
Pour savoir à partir de combien d'entrées de films il vaut mieux passer à l'abonnement, on peut effectuer un petit calcul. Il consiste à savoir pour quelle valeur les deux fonctions ont la même image. Pour cela, il faut résoudre l'équation f(x) = g(x).
Cela donne :
Le résultat de 6 indique que le point de bascule entre les deux fonctions arrive quand x = 6. Cela signifie que l'offre sans abonnement est avantageuse jusqu'à 6 places. Ensuite, il vaut mieux se tourner vers la version avec abonnement.
Quelle différence entre une fonction affine et une fonction linéaire ?
Faire la distinction entre fonction affine et fonction linéaire est primordial car c'est à l'origine de nombreuses confusions de la part des élèves.
Il existe bel et bien un lien entre ces deux fonctions : toutes les fonctions linéaires sont des fonctions affines. Mais attention, l'inverse n'est pas vrai ! La fonction linéaire est une fonction particulière, dans laquelle b = 0.
Définitions et différences graphiques
Pour faire une différence mathématique entre la fonction affine et la fonction linéaire, il y a une solution simple, l'origine du repère sur la représentation géométrique.
En effet, la fonction linéaire a pour formule f(x) = a x, c'est une fonction de proportionnalité. C'est pourquoi quel que soit a, la droite de f(x) passe toujours par l'origine : le point (0 ; 0).
Dans le cas d'une fonction affine, la formule étant f(x) = a x + b, si b ≠ 0, alors la droite de f(x) coupera forcément l'axe des ordonnées en un point autre que 0. La droite sera donc "décalée" de l'origine, coupant l'axe à la hauteur de b.
Pour récapituler toutes ces différences, voici un tableau à retenir :
| Caractéristique | Fonction linéaire | Fonction affine |
|---|---|---|
| Formule | f(x) = a x | f(x) = a x + b |
| Ordonné à l'origine (b) | b = 0 | b ≠ 0 |
| Représentation graphique | Passe par l'origine (0 ; 0) | Ne passe pas par l'origine |
| Logique mathématique | Proportionnalité | Proportionnalité des accroissements |
| Exemple | f(x) = 5x | f(x) = 5x + 3 |
Cas concrets d’utilisation
Voyons maintenant des cas concrets dans lesquels les fonctions affines et linéaires sont utilisées.
Exemple d'une fonction linéaire : la tarification proportionnelle.
Ce genre de fonction s'utilise quand il n'y a aucun frais de départ et que l'on ne paye que ce que l'on consomme.
Chez le maraîcher, les pommes de terre sont à 3 € le kilo. Quel prix allons-nous payer si l'on achète 5 kilos ?
Pour résoudre ce problème, on peut décrire la fonction f(x) = 3x. Calculons f(5) = 3 x 5 = 15. Pour acheter 5 kilos de pommes de terre, cela nous coûtera 15 €.
Exemple d'une fonction affine : le tarif fixe avec coût variable
On utilisera une fonction affine quand une partie fixe s'ajoute à ce que l'on consomme.
Prenons l'exemple d'un abonnement téléphonique. L'abonnement est de 20 € par mois et vous payez en plus 0,10 € la minute d'appel. Combien allez-vous payer si vous téléphonez 1h ?
Soit la fonction g(x) = 0,10 x + 20. 1h d'appel équivaut à 60 minutes. Calculons g(60) = 0,10 x 60 + 20 = 6 + 20 = 26 €.
Si vous téléphonez 1h avec cet abonnement, cela vous coûtera 26 €.
Fonction affine : exercices pratiques
Pour vérifier que vous avez bien compris, voici trois exercices types avec leurs corrections détaillées.
Exercice 1 : Identifier les coefficients
Soit la fonction affine définie par : f(x) = - 4x + 7
- Quel est le coefficient directeur ?
- Quelle est l'ordonnée à l'origine ?
- La fonction est-elle croissante ou décroissante ?
- Le coefficient directeur est le nombre qui multiplie x, donc a = - 4.
- L'ordonnée à l'origine est la constante ajoutée, donc b = 7.
- Comme a est négatif (- 4 < 0), la fonction est décroissante.
Exercice 2 : Calculer une image et un antécédent
Soit la fonction g(x) = 3x - 5
- Calculer l'image de 4.
- Trouver l'antécédent de 10.
- Image de 4 : On remplace x par 4. g(4) = 3 × 4 - 5 = 12 - 5 = 7.
- Antécédent de 10 : On cherche x tel que 3x - 5 = 10.
3x = 10 + 5
3x = 15
x = 15 / 3
x = 5.
Exercice 3 : Le problème du plombier
Un plombier facture 40 € le déplacement (prix fixe) et 30 € par heure de main-d'œuvre.
- Déterminer la fonction h(x) qui représente le prix total à payer pour x heures de travail.
- Combien coûtera une intervention de 2 heures ?
- La partie variable est 30 € par heure (30x) et la partie fixe est 40 €. La fonction est donc : h(x) = 30x + 40.
- Pour 2 heures (x=2) : h(2) = 30 × 2 + 40 = 60 + 40 = 100 €.
Résumer avec l'IA :
Vous avez aimé cet article ? Notez-le !
Loading...
Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !