Chapitres
Les mathématiques font partie prenante de nos vies. Pour les utiliser, les expressions numériques sont primordiales. Aujourd’hui, apprenez avec nous comment effectuer les opérations courantes et calculer rapidement des expressions simples !
Que ce soit pour réussir vos exercices ou simplement une recette de cuisine, apprenez les règles de calcul et les méthodes pour devenir incollable sur le sujet ! Gagner en confiance sur ces opérations vous permettra également d’être plus efficace au quotidien.
Comprendre les expressions numériques
Une expression numérique est une chaîne de nombres reliés entre eux par des opérateurs mathématiques. Ces derniers se comptent au nombre de 4 et ont chacun un symbole qui y est associé.
Ce tableau détaille les 4 opérateurs mathématiques qui entrent dans la composition des expressions numériques.
| Opérateur | Symbole |
|---|---|
| Addition | + |
| Soustraction | - |
| Multiplication | × |
| Division | ÷ |
On peut aussi trouver des séparateurs dans ces expressions numériques qui sont représentés par des parenthèses. Elles permettent d’ordonner les calculs au sein de l’expression numérique.
Attention à ne pas confondre les expressions numériques et les expressions littérales.
Les expressions numériques
Elles se limitent à utiliser les nombres sans aucune lettre. Elles permettent de représenter des opérations simples ou complexes mais sans variable. Les seuls symboles que l'on peut y trouver sont les opérateurs suivants :
+
-
×
÷
Les expressions littérales
Ce sont des expressions mathématiques qui utilisent des lettres pour représenter des nombres inconnus que l'on appelle "variables".
On utilise en général les variables en mathématiques afin d’énoncer des règles générales ou des expressions dont les valeurs peuvent changer.
Les règles de calcul des expressions numériques
Dans les expressions numériques, les calculs doivent s’effectuer dans un ordre précis.
Ordre 1
Les opérations à l’intérieur des parenthèses
Ordre 2
Les calculs d’exponentiation
Ordre 3
Les opérations de multiplication et de division, de gauche à droite
Ordre 4
Les opérations d’addition et de soustraction de gauche à droite
Les parenthèses
Les parenthèses servent à ordonner les calculs. Elles sont les premières dans l’ordre de priorité de calcul des expressions numériques.
Pour comprendre leur utilité, voyons un exemple. Imaginons que vous voulez calculer le prix d’achat de 5 livres à 10 € avec des frais de livraison de 3 €. L’opération à effectuer sera :
✅ 5 x 10 € + 3 € = 53,00 €
Maintenant, imaginons que vous achetez deux lots de 5 livres comme précédemment. On utilisera alors la formule :
✅ 2 x (5 x 10 €) + 3 € = 103,00 €
Dans notre cas, l’utilisation des parenthèses permet de multiplier par 2 uniquement le prix des livres et non celui de la livraison. Si nous avions multiplié par deux la totalité de l’expression d’origine, le résultat aurait été incorrect :
❌ 2 x (5 x 10 € + 3 € ) = 106,00 €
L’exponentiation
L’opération d’exponentiation est une opération mathématique qui consiste à calculer le résultat de la multiplication d’un nombre par lui même un certain nombre de fois.
Cette opération se place en second dans l’ordre de calcul des expressions numériques.
Il est noté an :
a est appelé la base
n est appelé l'exposant
Il existe certaines exponentiations remarquables. Par exemple :
Quand n=2
On parle d'élever un nombre au carré
Quand n=3
On parle d'élever un nombre au cube
Pour en savoir plus, vous pouvez consulter notre article sur les puissances mathématiques.
Ce tableau reprend quelques exemples d’exponentiations :
| a | n | Résultat de an |
|---|---|---|
| 2 | 1 | 21 = 2 |
| 2 | 2 | 2 2 = 4 |
| 2 | 3 | 2 3 = 8 |
| 2 | 0 | 2 0 = 1 |
| 10 | 4 | 10 4 = 10 000 |
| 5 | 10 | 5 10 = 9 765 625 |
✅ Un nombre à la puissance 0 est toujours égal à 1
✅ Un nombre à la puissance 1 est toujours égal à lui-même
La multiplication et la division
Les opérations de multiplication et de division arrivent en troisième place dans l’ordre de calcul des expressions numériques. Ces deux opérations travaillent ensemble puisqu’elles sont inverses l’une de l’autre.
Multiplier un nombre
Cela consiste à additionner plusieurs fois le même nombre.
Diviser un nombre
Cela consiste à calculer le nombre de fois qu'il faut multiplier un nombre pour en obtenir un autre.
D’ailleurs, il est possible d’utiliser la division pour vérifier le résultat d’un calcul d’une multiplication et inversement. Voyons quelques exemples :
- Si l’on effectue le calcul suivant : 235 x 42 = 9 870
- Alors on peut vérifier que c’est le bon résultat en contrôlant que
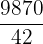est bien égal à 235
Pour résumer :
- Afin de contrôler que a x b = c
- Vérifiez que
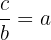
En mathématiques, tout est logique : il est fréquent que l’on puisse facilement vérifier le résultat d’une opération en effectuant l’opération inverse.
L’addition et la soustraction
Les additions et les soustractions sont les opérations que l’on effectue le plus. Cependant, elles interviennent en tout dernier dans l’ordre de calcul. Tout comme la multiplication et la division, l’addition et la soustraction sont complémentaires. En effet, soustraire un nombre consiste à additionner un nombre négatif.
Elles seront donc les dernières à prendre en compte dans le calcul d’une expression, de la gauche vers la droite.
Pour faire simple : 10 - 2 = 10 + (-2) = 8.
Simplifier les expressions numériques
En mathématiques, simplifier une expression numérique signifie la réduire au maximum sans en modifier le résultat. Pour ce faire, il faut appliquer plusieurs méthodes.
Pour simplifier une expression, il suffit de suivre quelques étapes simples :
- Regrouper les termes similaires ;
- Factoriser ;
- Transformer les soustractions en additions.
Voyons maintenant de manière détaillée comment effectuer chacune de ces étapes de simplification des expressions numériques.
Regrouper les termes similaires
Quand une expression numérique contient des additions et des soustractions, regrouper les nombres positifs et négatifs entre eux permet de s’y retrouver plus facilement. Il s’agit de la première étape de la simplification.
Pour cela :
- Commencez par regrouper tous les nombres positifs en les additionnant
- Puis ensuite, soustrayez tous les nombres négatifs
Cela permettra d’éviter les erreurs de signes dans la suite des calculs.
Par exemple, l’expression : 2 + 5 + (-4) + 2 + (-1) peut se simplifier en 2 + 5 + 2 - 4 - 1.
Factoriser
Factoriser une expression signifie la transformer en produit de facteurs, avec un facteur commun. Cela permet de raccourcir grandement les expressions numériques constituées de beaucoup de multiplications. Grâce à la mise en évidence du facteur commun, vous pourrez même diminuer les calculs et ainsi réduire les risques de se tromper.
Prenons en exemple une expression numérique : 2 x 3 + 5 x 2 + 2 x 1. Cette dernière, une fois factorisée, donne 2 x (3 + 5 + 1).
Transformer les soustractions en additions
Soustraire un nombre revient à ajouter son opposé. En effet :
- 10 - 2 = 10 + (- 2) = 8
Cela nous donne la possibilité de transformer l’expression numérique :
- 15 - 4 + 6 - 1 en 15 + (- 4) + 6 + (- 1)
- Puis (15 + 6) + (- 4 + - 1)
On peut ensuite aisément calculer l’intérieur des parenthèses tout en limitant les erreurs de calcul dues aux différents signes mais aussi d’appliquer les règles de priorité de manière plus simple.
Calculer avec les expressions numériques dans la vie de tous les jours
Savoir utiliser les expressions numériques et les calculer vous sera non seulement utile pour vos cours de mathématiques, pour le brevet ou le baccalauréat mais cela vous sera aussi utile dans la vie courante !
Voyons quelques exemples.
Calculer une réduction
Ce sont les soldes et vous avez flashé sur ce superbe manteau en laine ! Il coûte 179,99 €, ce qui est beaucoup trop cher… Mais heureusement, un petit coupon est accroché dessus : -30 %. Vous avez 140 € dans votre porte-feuille. Pouvez-vous acheter ce magnifique manteau ?
Tout d’abord, il faut appliquer la réduction. Pour cela, effectuons le calcul suivant :
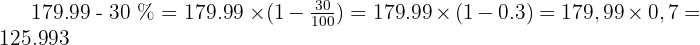
Cela donne un manteau à 125,99 €. Ouf, c’est accessible avec le contenu du porte-monnaie !
Calculer des aires
Quand vous aurez besoin de repeindre un mur, vous devrez calculer la surface (l’aire) de ce que vous devez peindre.
Prenons une pièce carrée avec des murs de 4 m sur 2 m. Un bidon de peinture de 10 L permet de couvrir 10 m2. Nous allons calculer le nombre de pots de peinture nécessaire.
Pour commencer, calculons la surface de la pièce :
- 1 pan de mur = 4 x 2 = 8 m2
- Donc les 4 murs représentent 8 x 4 = 32 m2
Divisons la surface à peindre par 10 pour savoir le nombre de bidons nécessaires :
- 32 / 10 = 3,2 bidons
Nous devrons donc acheter 4 bidons pour tout couvrir.
Faire des recettes de cuisine
Pour faire un gâteau, vous trouvez aisément des recettes. Mais pas forcément pour le bon nombre de convives… Imaginons que vous souhaitez faire un gâteau au chocolat mais que vous n’avez trouvé qu'une recette que pour 4 personnes. Mais à votre anniversaire vous invitez 6 personnes. Il faut donc calculer les bonnes quantités.
Un calcul simple permet de passer les quantités de 4 à 6 personnes. Nous allons utiliser pour cela un coefficient multiplicateur. Pour cela, rien de plus simple :
- Divisons 6 par 4, ce qui donne 1,5
- Il ne reste plus qu’à multiplier chaque quantité pour 4 personnes par 1,5 et nous aurons la quantité nécessaire pour 6
On obtient donc le tableau suivant :
| Quantité pour 4 personnes | Quantité pour 6 personnes | |
|---|---|---|
| Chocolat | 100 g | 150 g |
| Beurre | 70 g | 105 g |
| Sucre | 80 g | 120 g |
| Oeufs | 2 | 3 |
| Farine | 40 g | 60 g |
| Sel | 1 pincée | 1,5 pincées |
| Sucre vanillé | 1 cuillère | 1,5 cuillères |
Il ne vous reste plus qu’à enfiler votre tablier !
S'entraîner avec les expressions numériques
Méthode à retenir pour calculer
Pour utiliser correctement les expressions numériques dans vos exercices de mathématiques, il faut donc procéder par ordre :
- Identifier l’expression numérique ;
- Repérer les opérateurs et les parenthèses ;
- Appliquer les règles de priorité suivantes :
- Calculer entre parenthèses ;
- Calculer les multiplications et les divisions ;
- Calculer les additions et les soustractions.
Vous pouvez ensuite réduire l’expression numérique si besoin afin de la rendre plus lisible ou plus simple à calculer.
Des exercices sur les expressions numériques pour mieux comprendre
Calculer les expressions suivantes en faisant attention à l’ordre de priorité des calculs.
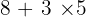
Ce champ est requis.
La réponse est 23.
Il faut calculer :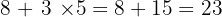 
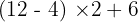
Ce champ est requis.
La réponse est 22.
Il faut calculer :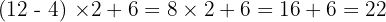 
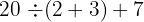
Ce champ est requis.
La réponse est 11.
Il faut calculer :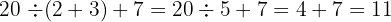 
Calculer et simplifier si possible les expressions suivantes.
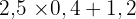
Ce champ est requis.
La réponse est 2,2.
Il faut calculer :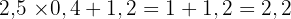 
Calculer les expressions suivantes.
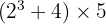
Ce champ est requis.
La réponse est 60.
Il faut calculer :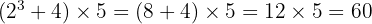 
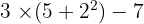
Ce champ est requis.
La réponse est 20.
Il faut calculer :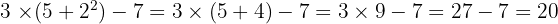 
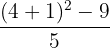
Ce champ est requis.
La réponse est 3,2.
Il faut calculer :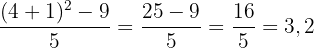 
Testez vos connaissances sur les expressions numériques
Vérifiez si vous avez bien retenu ce qu'il faut savoir sur les expressions numériques ! Si vous connaissez la réponse, cliquez sur ✅. Si vous ne la connaissez pas, cliquez sur ❌. Vous pouvez retourner la carte pour connaître la réponse.
6 + 3 × 4 ?Vous avez aimé cet article ? Notez-le !
Loading...
Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Très bien mais un peu complexe