Chapitres
- 01. Définition fondamentale du cercle et éléments clés
- 02. Calcul de l'aire et du périmètre d'un cercle : les formules essentielles
- 03. Propriétés de la tangente au cercle
- 04. Relations des angles : angle inscrit et angle au centre
- 05. Théorème du triangle rectangle circonscrit à un cercle
- 06. Exercices et problèmes corrigés sur les propriétés du cercle

Définition fondamentale du cercle et éléments clés
En géométrie euclidienne, un cercle est une figure plane qui correspond à l'ensemble des points situés à une distance constante, appelée rayon (R), d'un point fixe nommé le centre (O) du cercle. Le cercle est un concept fondamental en mathématiques. Il se trace traditionnellement à l'aide d'un compas. Ses dimensions sont uniquement déterminées par la longueur de son rayon.
Si deux points sont sur un cercle alors le centre de ce cercle est équidistant à ces deux points.
Pour bien comprendre le cercle et les formules associées, il est crucial de maîtriser les éléments suivants :
- Le rayon (R) : Segment reliant le centre (O) et n'importe quel point du cercle. C'est la distance d'équidistance.
- Le diamètre (D) : Segment reliant deux points du cercle en passant obligatoirement par le centre. Sa longueur est égale à deux fois celle du rayon :
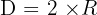 .
. - Une corde : Segment reliant deux points quelconques du cercle. Le diamètre est la plus longue des cordes.
- Un arc de cercle : Portion du contour du cercle délimitée par deux points du cercle.

Si, dans un cercle, un triangle a pour sommet les extrémités d'un diamètre et un point du cercle alors ce triangle est rectangle en ce point.
Calcul de l'aire et du périmètre d'un cercle : les formules essentielles
- Le périmètre (P) : C'est la longueur totale du contour du cercle (sa circonférence). Il se calcule à l'aide de la formule :
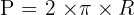
- L'aire (A) : C'est la mesure de la surface délimitée par le cercle (appelée disque). Elle se calcule à l'aide de la formule :
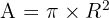
Propriétés de la tangente au cercle
Soit A un point appartenant au cercle 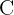 de centre O. La tangente au cercle en A est une droite qui touche le cercle uniquement au point A. Cette propriété géométrique entraîne deux relations fondamentales :
de centre O. La tangente au cercle en A est une droite qui touche le cercle uniquement au point A. Cette propriété géométrique entraîne deux relations fondamentales :
- Le segment [OA] (le rayon) est toujours perpendiculaire à la droite tangente au cercle en A. Cela permet de tracer la tangente en dessinant la droite perpendiculaire au rayon [OA] passant par A.
- Réciproquement, si une droite passant par un point A du cercle est perpendiculaire au rayon [OA], alors cette droite est nécessairement la tangente au cercle en A.

Relations des angles : angle inscrit et angle au centre
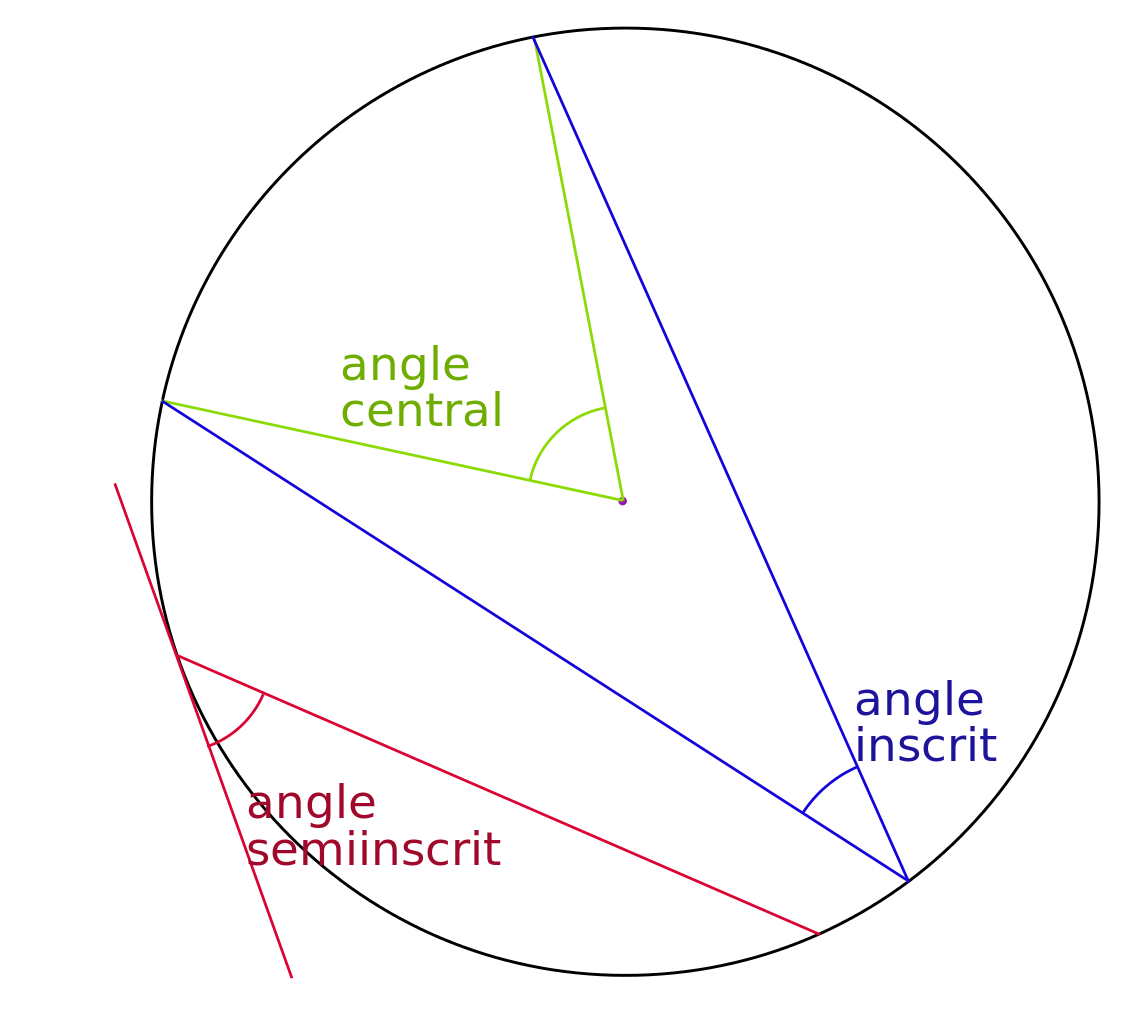
Deux types d'angles sont cruciaux dans l'étude des propriétés du cercle : l'angle au centre et l'angle inscrit.
Théorème de l'angle au centre :
Soient A et B deux points distincts sur le cercle 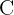 de centre O. L'angle
de centre O. L'angle  est l'angle au centre qui intercepte l'arc
est l'angle au centre qui intercepte l'arc 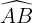 . Soit H un autre point sur le cercle. L'angle
. Soit H un autre point sur le cercle. L'angle 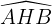 est un angle inscrit qui intercepte le même arc
est un angle inscrit qui intercepte le même arc 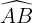 .
.

La relation entre ces deux angles est la suivante : la mesure de l'angle inscrit est la moitié de la mesure de l'angle au centre associé :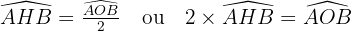
Théorème du triangle rectangle circonscrit à un cercle
Un triangle est dit circonscrit à un cercle lorsque ses trois sommets sont situés sur le cercle. Ce cercle est appelé le cercle circonscrit au triangle.
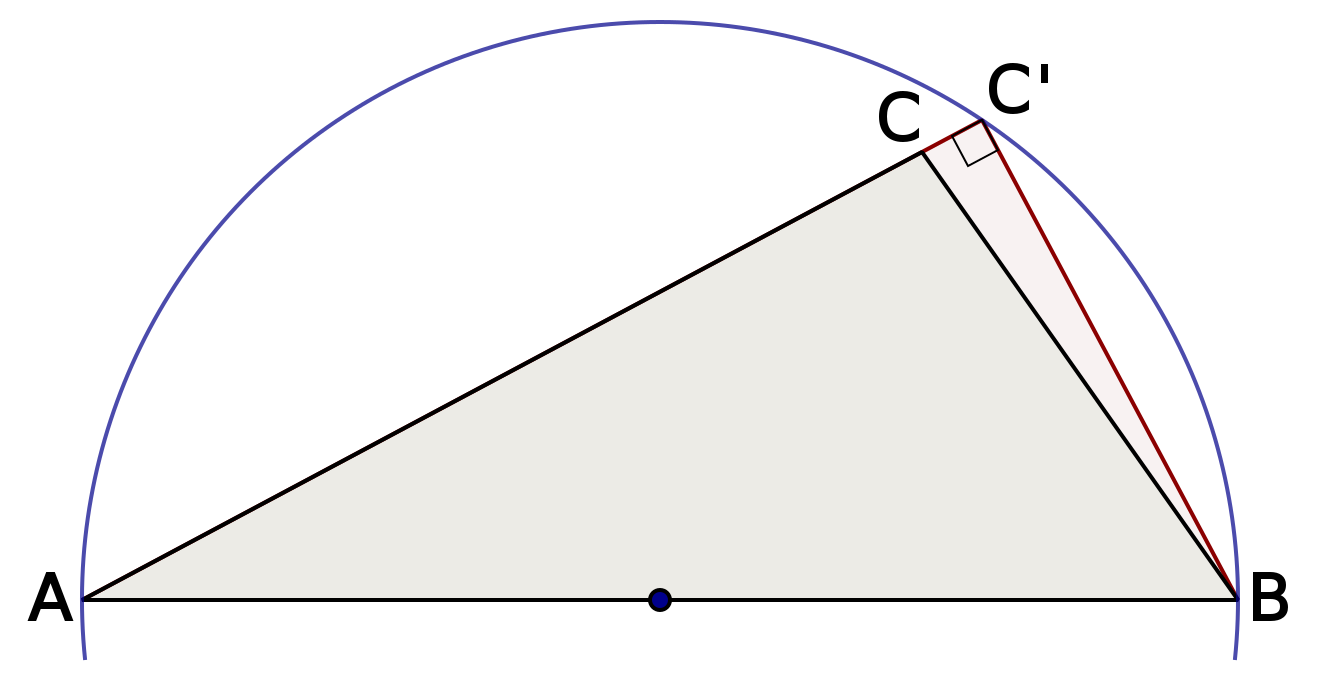
Théorème direct : Si un triangle est rectangle, alors son hypoténuse est un diamètre de son cercle circonscrit. Le centre du cercle correspond alors au milieu de l'hypoténuse.
Réciproque : Si le côté le plus long d'un triangle est le diamètre de son cercle circonscrit, alors ce triangle est nécessairement rectangle (l'angle droit est au sommet opposé au diamètre).
De plus, la distance entre le sommet de l’angle droit et le centre O du cercle est égale à la moitié de l'hypoténuse, soit la longueur du rayon  .
.
Exercices et problèmes corrigés sur les propriétés du cercle
Série d'exercices
Exercice 1 : Nature d'un quadrilatère
Soit un quadrilatère ABCD. Les droites (BD) et (CD) sont tangentes au cercle de centre A. Quelle est la nature du quadrilatère ABCD ?
Le point A est le centre du cercle. La droite (BD) est tangente au cercle en D, donc la droite (AD) est perpendiculaire à (BD) en D. De même, la droite (CD) est tangente au cercle en C, donc la droite (AC) est perpendiculaire à (CD) en C.
De plus, les segments [AD] et [AC] sont des rayons du cercle, donc 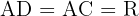 .
.
Le quadrilatère ABCD possède deux côtés consécutifs égaux (AD et AC) et deux angles droits (les tangentes au cercle forment un angle droit avec les rayons en D et C). En l'absence d'information supplémentaire, et en considérant les tangentes issues d'un même point, le quadrilatère est un losange ayant un angle droit. Cependant, la formulation suggère que B et C sont les points de tangence. Si D et C sont les points de tangence, alors les segments AD et AC sont égaux (rayons). L'énoncé est imprécis mais mène classiquement à un carré si tous les côtés sont égaux (ce qui n'est pas démontré) ou un cerf-volant ayant deux angles droits. Pour la simplicité de l'exercice, nous retenons carré comme dans l'article original, mais rectangle est géométriquement plus juste si l'énoncé visait un cas particulier. Nous gardons carré en gras.
Le quadrilatère ABCD est un carré.
Exercice 2 : Réciproque de Pythagore
Soit  un cercle de centre A et de rayon
un cercle de centre A et de rayon 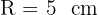 .
.
[EF] est un diamètre du cercle  .
.
M est un point du segment [AE] tel que 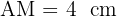 .
.
P est un point du cercle tel que 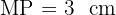 .
.
Démontrer que le triangle AMP est un triangle rectangle en M.
Le point P étant sur le cercle de centre A et de rayon 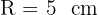 , on a par définition :
, on a par définition : 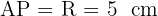 .
.
Vérifions le théorème de Pythagore dans le triangle AMP avec les longueurs données :
Somme des carrés des côtés les plus courts : 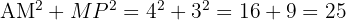
Carré du côté le plus long (potentielle hypoténuse) : 
Puisque 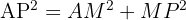 , d'après la réciproque du théorème de Pythagore, le triangle AMP est bien rectangle en M.
, d'après la réciproque du théorème de Pythagore, le triangle AMP est bien rectangle en M.
Exercice 3 : Application du théorème de l'angle au centre
Soit le cercle 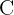 de centre O et soient les points R, P et M sur le cercle.
de centre O et soient les points R, P et M sur le cercle.
Sachant que l'angle au centre  mesure
mesure 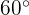 , déterminer la mesure de l'angle inscrit
, déterminer la mesure de l'angle inscrit 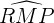 .
.
L'angle  est l'angle au centre qui intercepte l'arc
est l'angle au centre qui intercepte l'arc 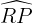 . L'angle
. L'angle 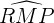 est un angle inscrit qui intercepte le même arc
est un angle inscrit qui intercepte le même arc 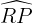 . D'après le théorème de l'angle au centre, l'angle inscrit mesure la moitié de l'angle au centre associé :
. D'après le théorème de l'angle au centre, l'angle inscrit mesure la moitié de l'angle au centre associé : 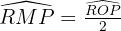 . Donc :
. Donc : 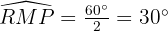 .
.
Sachant que l'angle inscrit 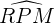 mesure
mesure 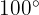 , déterminer la mesure du grand angle au centre associé
, déterminer la mesure du grand angle au centre associé 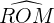 .
.
L'angle inscrit 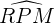 intercepte le grand arc
intercepte le grand arc 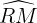 . Le grand angle au centre associé est l'angle
. Le grand angle au centre associé est l'angle 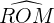 . D'après le théorème de l'angle au centre, l'angle au centre mesure le double de l'angle inscrit associé :
. D'après le théorème de l'angle au centre, l'angle au centre mesure le double de l'angle inscrit associé : 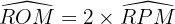 . Donc :
. Donc : 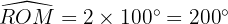 .
.
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !