Chapitres
L'étude de la position des droites est l'un des sujets fondamentaux de la géométrie, avec de nombreuses applications dans la vie courante.
Dans cet article, deux définitions sont importantes à connaître :
Parallélisme : deux droites sont dites parallèles si elles sont coplanaires et n'ont aucun point commun (strictement parallèles) ou si elles sont confondues.
Perpendicularité : deux droites sont perpendiculaires si elles sont sécantes et forment quatre angles de 90° au point d'intersection.
Ces critères permettent de confirmer le parallélisme et la perpendicularité entre deux droites dans des contextes variés.
| Critère | Deux droites sont parallèles si | Deux droites sont perpendiculaires si |
|---|---|---|
| Critère des pentes | Les pentes des deux droites sont égales (m1 = m2) | Le produit des pentes des deux droites est -1 (m1 * m2 = -1) |
| Critère des angles | Les angles que les deux droites forment avec une troisième droite sont égaux | Les angles que les deux droites forment avec une troisième droite sont des angles droits (90 degrés) |
| Critère des équations | Les équations des deux droites ont des coefficients directeurs identiques | Les équations des deux droites ont des coefficients directeurs dont le produit est -1 |

Démontrer que deux droites sont parallèles

Pour démontrer que deux droites sont parallèles, vous pouvez utiliser l'une des méthodes suivantes :
Méthode 1 : critère des pentes
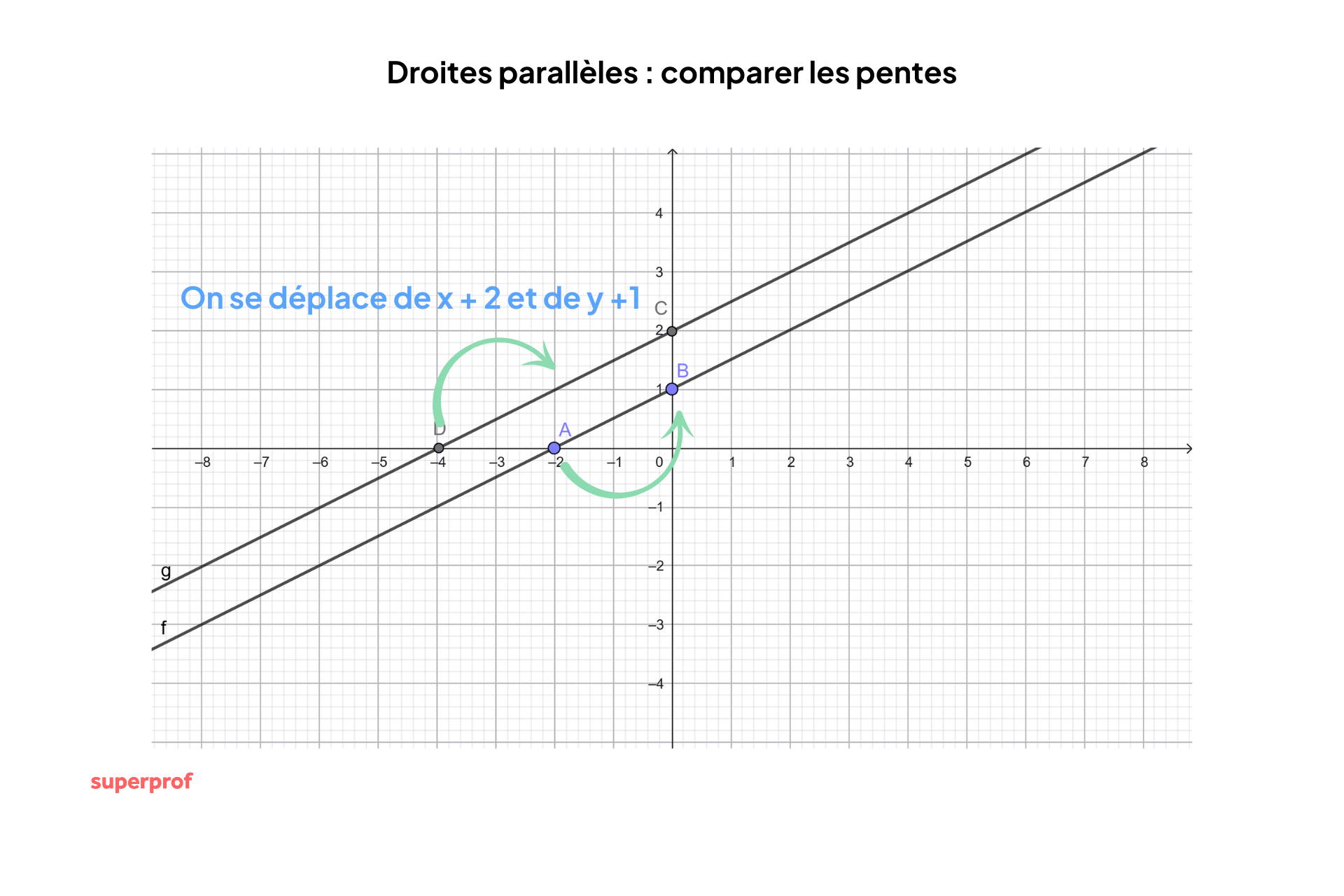
Si vous avez les équations des deux droites, vous pouvez donc comparer leurs pentes. Deux droites sont parallèles si et seulement si leurs pentes sont égales.
De façon logique, si les pentes des deux droites sont égales, vous pouvez conclure qu'elles sont parallèles.
Méthode 2 : critère des angles

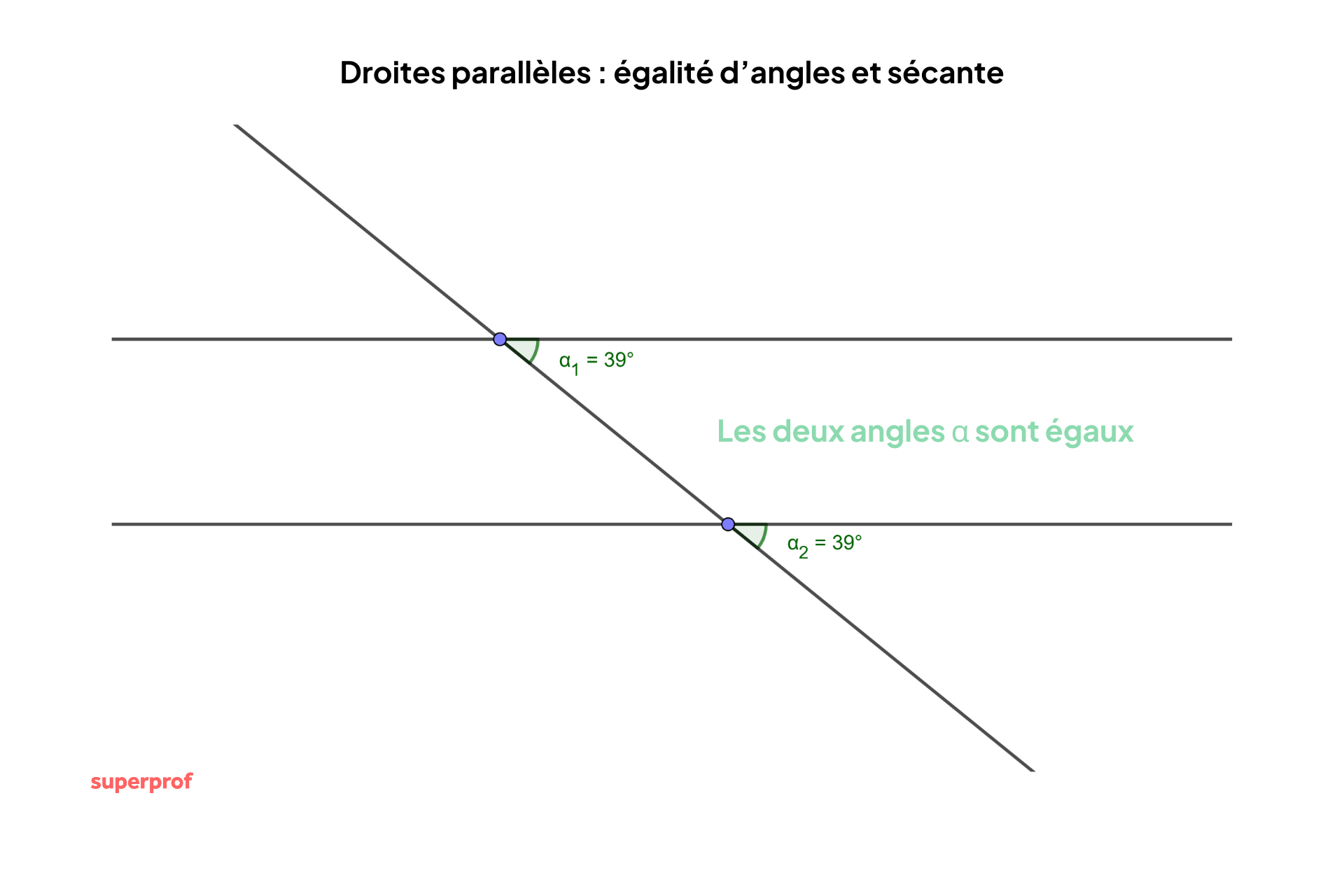
Si vous travaillez avec des segments de droites ou des droites non définies par des équations, vous pouvez utiliser les propriétés des angles pour montrer qu'elles sont parallèles.
? Deux droites sont parallèles si les angles qu'elles forment avec une troisième droite (appelée ligne de référence) sont égaux.
➡️ Exemple : Vous avez deux droites, (AB) et (CD), et une troisième droite (EF) comme ligne de référence. Si les angles ∠AEG et ∠CEH sont égaux, et les angles ∠DEI et ∠BGJ sont égaux, alors les droites (AB) et (CD) sont parallèles.
@dr.laaw #maths #brevetmaths #astucemaths #mathsfacile ♬ Let Me Down Slowly - 腾金涛
Méthode 3 : vecteurs colinéaires
Cette approche est utilisée en géométrie analytique et vectorielle lorsque les droites sont définies par des points dont on connaît les coordonnées et les vecteurs.
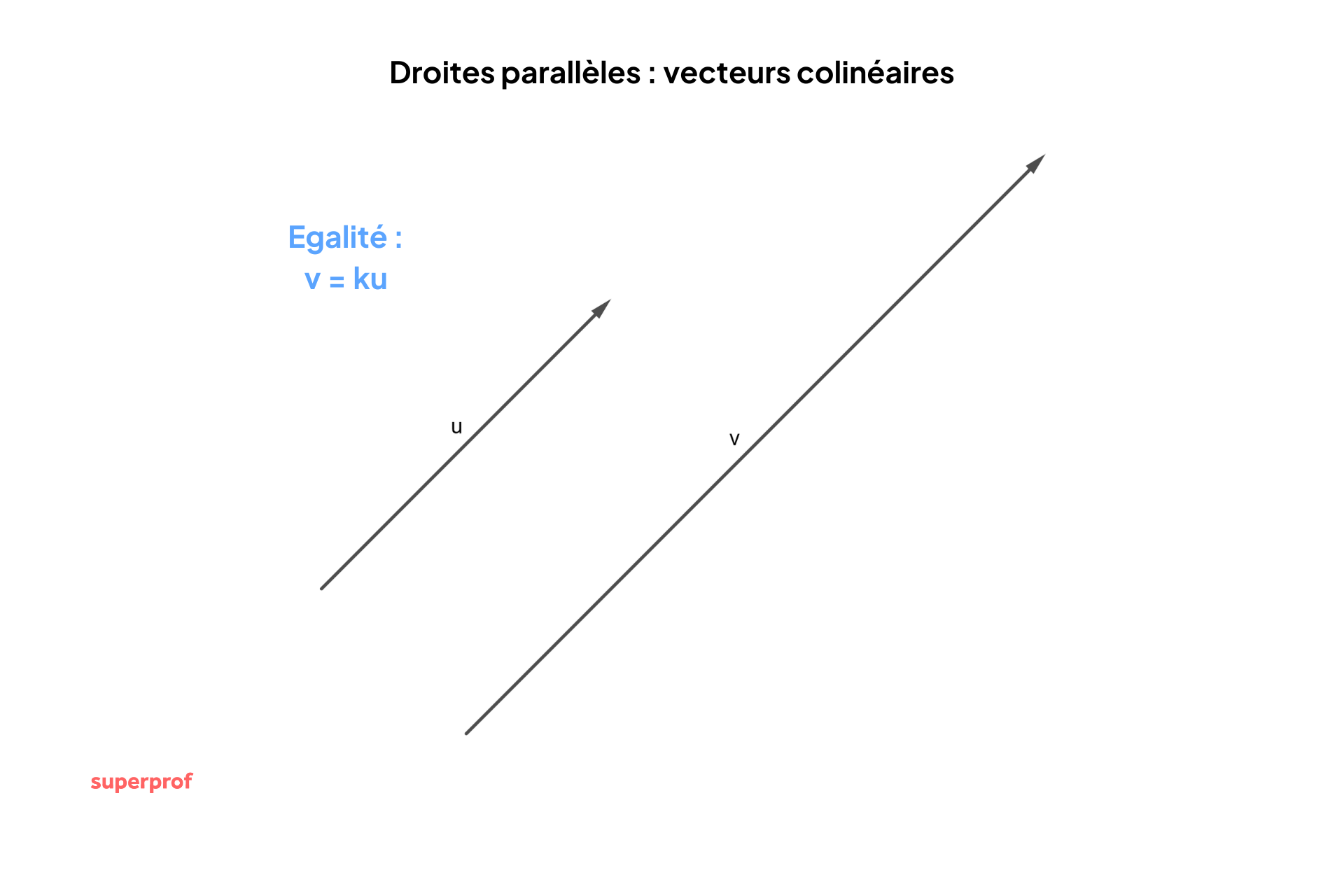
Deux droites sont parallèles si et seulement si leurs vecteurs directeurs sont colinéaires. Cela signifie que les vecteurs ont la même direction (bien que leur sens ou leur norme puissent différer). Algébriquement, cela implique que les coordonnées des vecteurs sont proportionnelles.
Voici la formule que cela implique :
Soient deux vecteurs directeurs u(x; y) et v(x'; y').
Les vecteurs sont colinéaires si leur déterminant est nul :
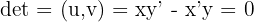
Ou, de manière équivalente, s'il existe un réel k tel que v = k x u.
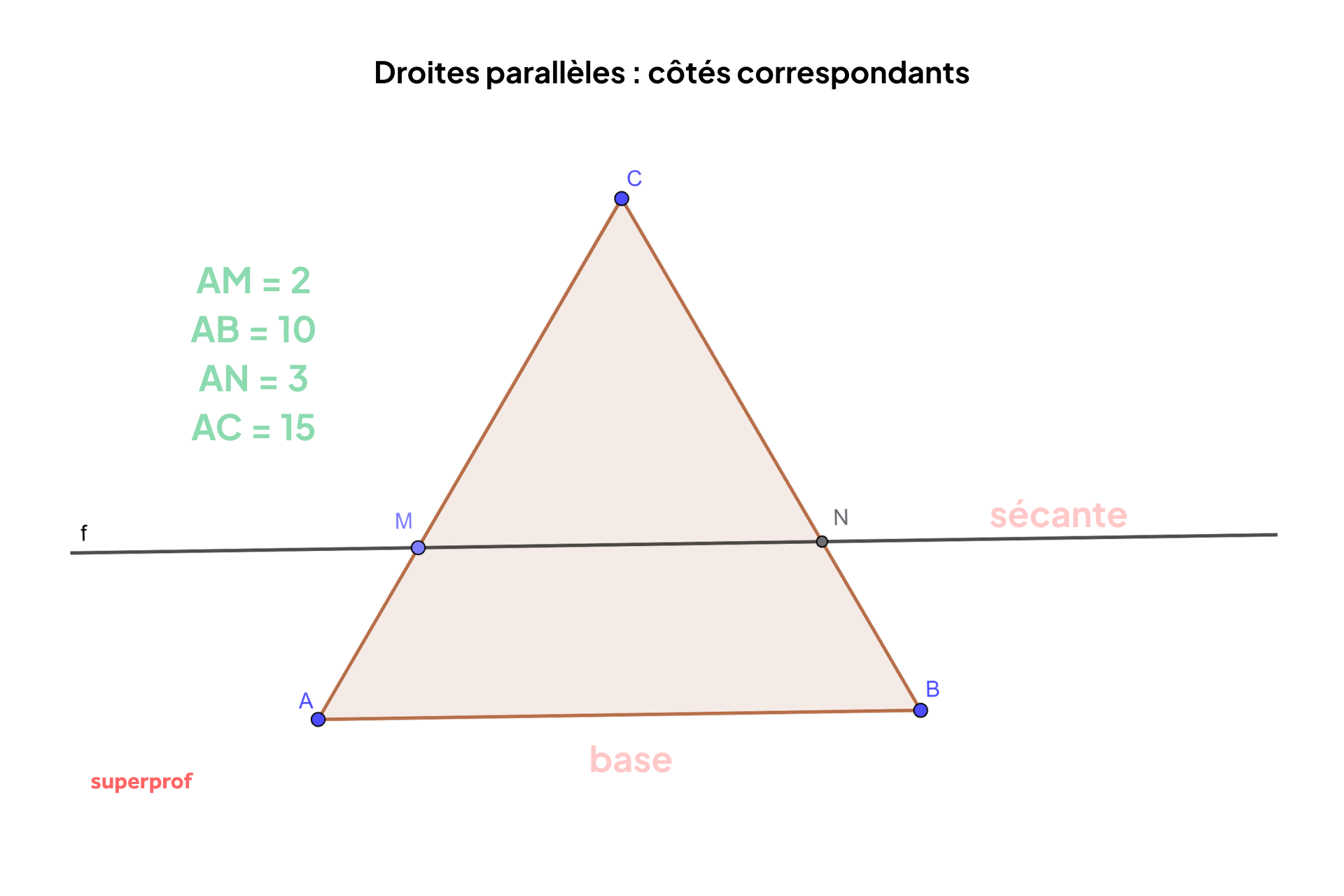
Méthode 4 : critère des côtés correspondants (propriété de Thalès)
Si vous travaillez avec des figures géométriques, vous pouvez montrer que deux droites sont parallèles en utilisant le critère des côtés correspondants.
Deux droites sont parallèles si les côtés correspondants de deux triangles sont proportionnels.
Exemple : Vous avez deux droites, (MN) et (PQ), et un troisième point O. Si les segments MO, NO, PO, et QO forment un quadrilatère où les côtés opposés sont parallèles, alors les droites (MN) et (PQ) sont parallèles.
Voici un tableau récapitulatif qui permet de trouver l'outil adapté selon les données disponibles :
| Méthode | Quand l'utiliser ? | Exemple d'application |
|---|---|---|
| Comparaison des pentes | Si les équations de droites sont connues (y = ax + b). | Vérifier que a1 = a2. |
| Angles et sécante | Si une troisième droite coupe les deux autres. | Identifier des angles alternes-internes égaux. |
| Vecteurs colinéaires | Dans un repère ou avec des coordonnées. | Calculer le déterminant de deux vecteurs (xy' - x'y = 0). |
| Théorèmes géométriques | Dans une figure (triangle, quadrilatère). | Utiliser la réciproque de Thalès ou la droite des milieux. |
Démontrer que deux droites sont perpendiculaires
Pour démontrer que deux droites sont perpendiculaires, vous pouvez utiliser le critère des pentes, le critère des angles, ou le critère des produits des pentes, en fonction des informations dont vous disposez.
Pour prouver que deux droites sont perpendiculaires, il suffit de démontrer que ces deux droites se coupent en un angle droit (90°).
Voici comment démontrer que deux droites sont perpendiculaires en utilisant chacune de ces méthodes :

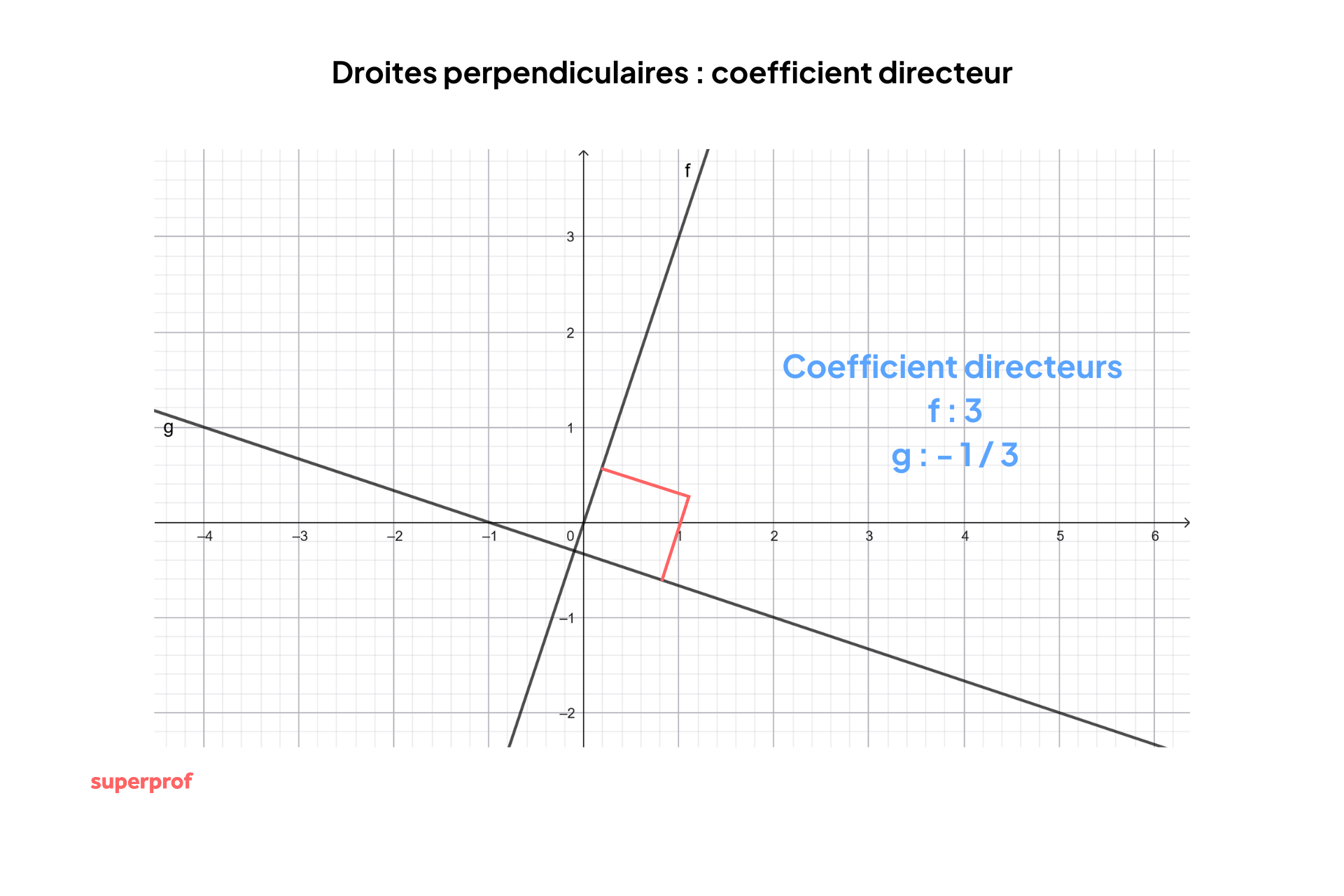
Méthode 1 : critère des pentes
Deux droites sont perpendiculaires si et seulement sile produit de leurs pentes est égal à -1. Autrement dit, si m1 et m2 sont les pentes de deux droites, alors elles sont perpendiculaires si m1 × m2 = -1.
➡️ Exemple : Droite 1 : y = 2x + 3 (pente m1 = 2) Droite 2 : y = -1/2x + 4 (pente m2 = -1/2)
Dans cet exemple, m1 × m2 = 2 × (-1/2) = -1, ce qui signifie que les deux droites sont perpendiculaires.
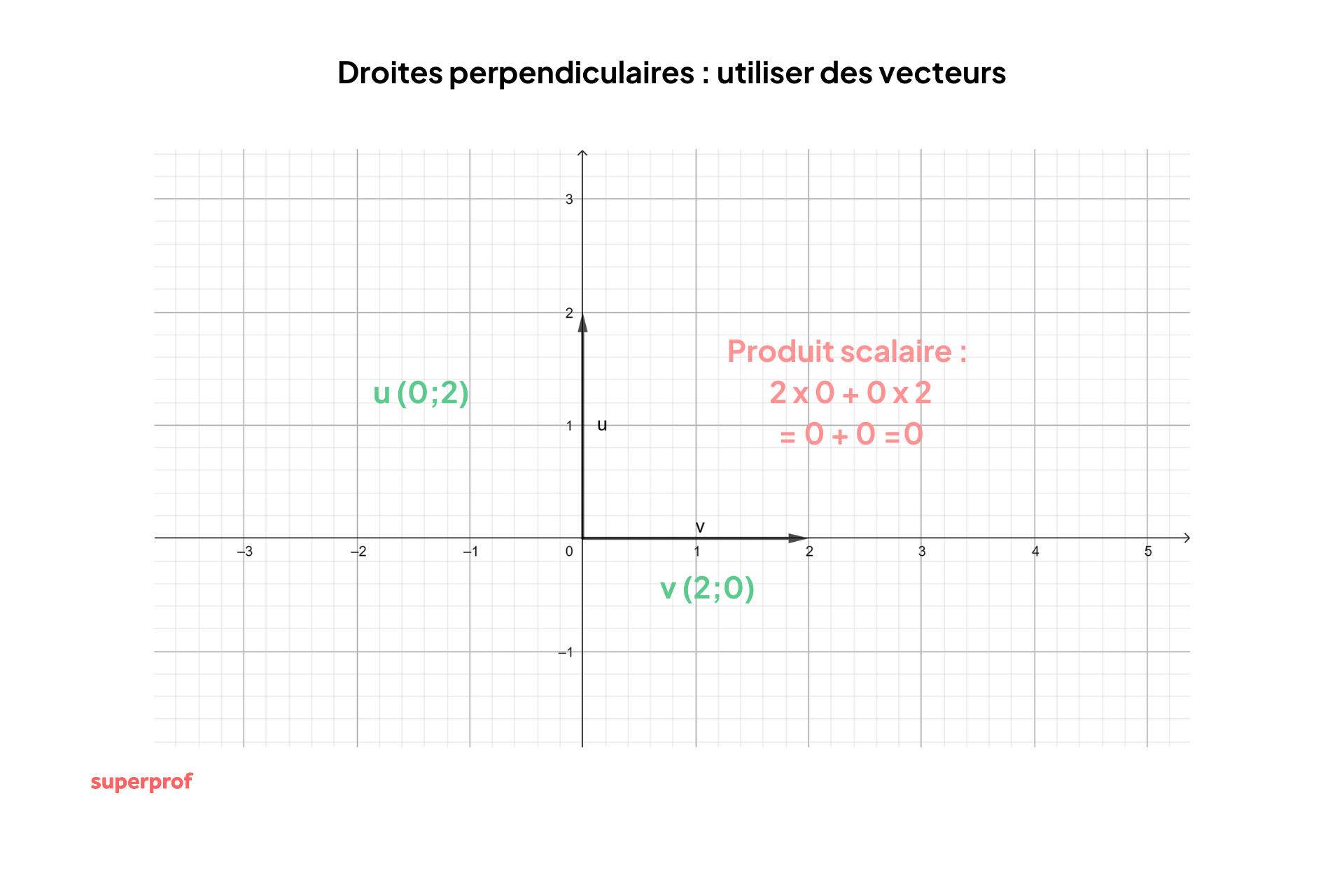
Méthode 2 : utiliser des vecteurs
La méthode des vecteurs est la plus puissante et celle la plus utilisée en physique et en ingénierie car elle peut s'appliquer en 2D et en 3D.
Afin de tester la perpendicularité (ou orthogonalité), on utilise le produit scalaire. Deux vecteurs non nuls sont orthogonaux si et seulement si leur produit scalaire est nul.
Voici la formule associée :
Soient u (x ; y) et v (x' ; y'), deux vecteurs directeurs.
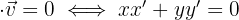
➡️ Exemple :
Méthode 3 : repérer un angle droit sur une figure
On utilise cette méthode en géométrie pure, lorsqu'on analyse des figures comme des cercles ou des triangles sans utiliser de coordonnées.
On déduit la perpendicularité en utilisant les théorèmes classiques qui prouvent la présence d'un angle de 90°.
Voici quelques cas classiques et théorèmes utiles :
- Réciproque du théorème de Pythagore : Dans un triangle, si le carré du plus grand côté est égal à la somme des carrés des deux autres (BC² = AB² + AC²), alors le triangle est rectangle en A et (AB) est perpendiculaire à (AC) ;
- Triangle et cercle circonscrit : Si un côté d'un triangle est le diamètre de son cercle circonscrit, alors ce triangle est rectangle ;
- Droites remarquables : Les hauteurs d'un triangle ou les médiatrices d'un segment sont perpendiculaires par définition.
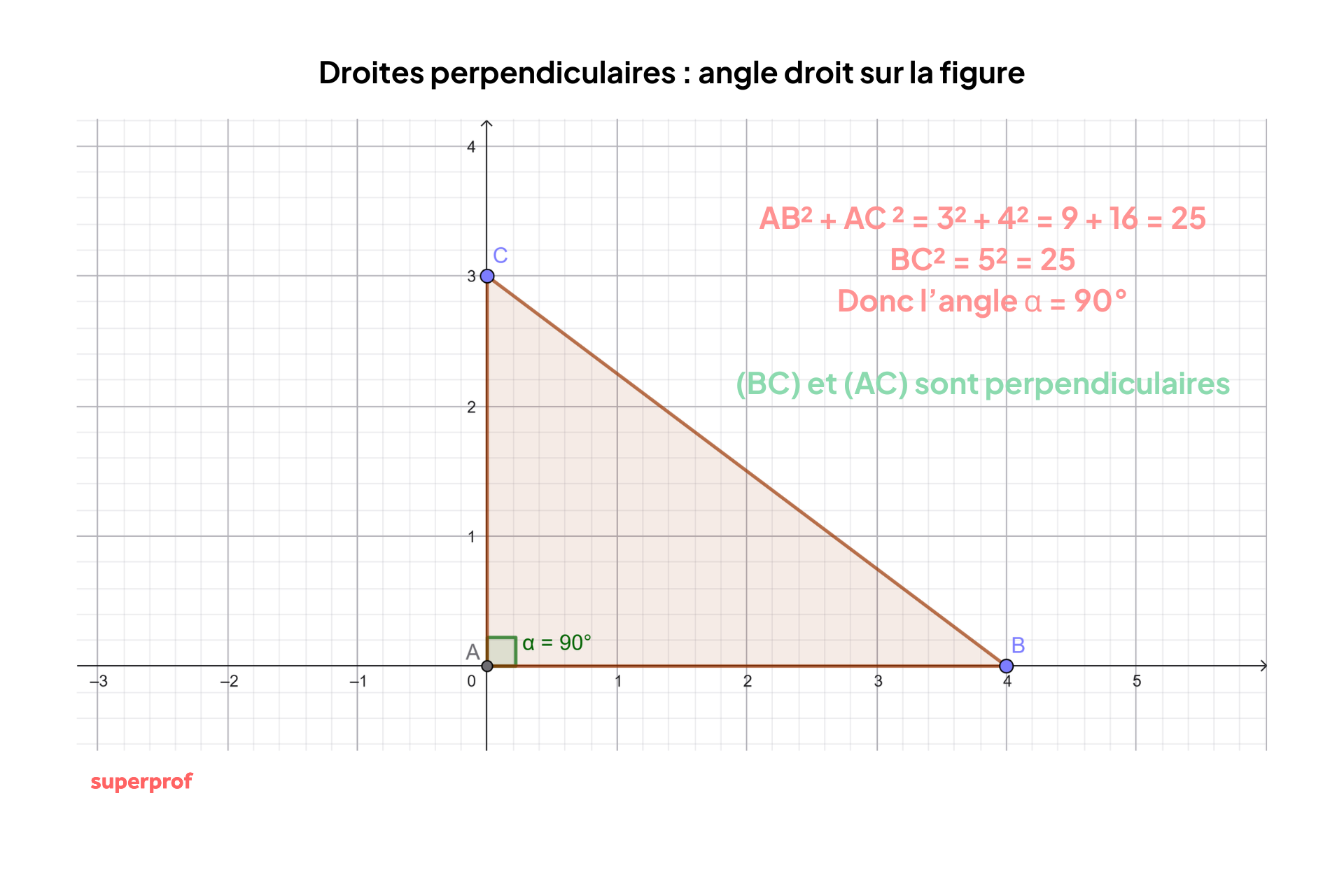
➡️ Exemple : avec le théorème de Pythagore :
Dans un triangle ABC, si AB=3, AC=4 et BC=5. On vérifie : 3² + 4² = 9 + 16 = 25 et 5² = 25. L'égalité est vérifiée, donc l'angle A est droit. Les droites (AB) et (AC) sont perpendiculaires.
Pour finir, voici là aussi un tableau récapitulatif qui vous aidera à choisir la méthode adaptée aux données dont vous disposez :
| Méthode | Quand l'utiliser ? | Condition mathématique |
|---|---|---|
| Produit des pentes | Si les droites sont définies par des équations (y = ax + b). | Le produit des coefficients directeurs vaut -1. |
| Produit scalaire | Si l'on dispose de vecteurs directeurs u et v. | Le produit scalaire est nul. |
| Propriétés géométriques | Dans une figure plane sans repère. | repère. Utilisation de Pythagore, d'un cercle circonscrit, ou des propriétés des médiatrices et hauteurs. |
Parallélisme : Vérifiez que les pentes sont égales (m = m′) ou que les vecteurs directeurs sont colinéaires (déterminant nul).
Perpendicularité : Vérifiez que le produit des pentes vaut -1 ou que le produit scalaire est nul.
Géométrie pure : Sans coordonnées, utilisez la réciproque de Thalès (parallèle) ou de Pythagore (perpendiculaire).
Exercices pour montrer que deux droites sont parallèles et perpendiculaires
La maîtrise des concepts géométriques ne s'acquiert véritablement qu'en confrontant la théorie à la résolution de problèmes. Après avoir détaillé les outils analytiques et les théorèmes fondamentaux, voyons maintenant comment vous savez utiliser ces nouveaux outils :
Démontrer que les droites (d) et (e) sont parallèles.
Énoncé : Soit un quadrilatère ABCD avec les côtés AB et CD. Les points E et F sont les milieux de ces côtés, c'est-à-dire que AE = EB et CF = FD. Les segments AC et BD se croisent en un point G. Vous devez démontrer que les droites (AG) et (EF) sont parallèles.
Consignes
Tracez un schéma clair du quadrilatère ABCD en plaçant les points A, B, C, et D.
Marquez les points E et F comme les milieux des côtés AB et CD, respectivement.
Tracez les segments AC et BD, qui se croisent en un point G.
Démontrez que les droites (AG) et (EF) sont parallèles en utilisant des arguments géométriques.
Pour démontrer que les droites (AG) et (EF) sont parallèles, nous allons utiliser la propriété des triangles semblables.
Commençons par noter que les segments AE, EB, CF et FD sont égaux, car E et F sont les milieux des côtés correspondants du quadrilatère ABCD. Cela signifie que AE = EB = CF = FD.
Maintenant, considérons les triangles AEG et FEG. Les deux triangles partagent un côté EG commun, et nous avons déjà établi que AE = EF et AG = FG (car G est le point d'intersection de AC et BD).
En utilisant le côté EG commun, les côtés proportionnels AE = EF et AG = FG, nous pouvons conclure que les triangles AEG et FEG sont semblables par le critère de la ressemblance des triangles (côté-côté-côté).
Lorsque deux triangles sont semblables, cela signifie que les angles correspondants sont égaux. Donc, les angles ∠AEG et ∠FEG sont égaux.
Maintenant, regardons le triangle EFG. Les angles ∠AEG et ∠FEG sont égaux, ce qui signifie que les angles opposés ∠GEF et ∠GFE dans le triangle EFG sont égaux.
En utilisant la propriété des angles opposés parallèles, si les angles ∠GEF et ∠GFE dans le triangle EFG sont égaux, alors les droites (AG) et (EF) sont parallèles.
Ainsi, nous avons démontré que les droites (AG) et (EF) sont parallèles à l'aide de la propriété des triangles semblables.
Sources
- Ministère de l'Éducation Nationale. "Programme de mathématiques de seconde générale et technologique." Bulletin officiel de l'éducation nationale, spécial n° 1, 22 janv. 2019. Éduscol, eduscol.education.fr/maths. Consulté le 29 janv. 2026.
- "Parallélisme (droites)." Bibmth.net, Dictionnaire de mathématiques, 2025, www.bibmath.net/dico/index.php. Consulté le 29 janv. 2026.
- Beltramone, Jean-Paul, et al. Déclic Mathématiques Seconde. Hachette Éducation, 2019. Consulté le 29 janv. 2026.
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
si les droites (AA) (BB) (CC) (DD) sont parallèles et coupent qu’on peut nous faire pour cela merci!
Bonjour, avez-vous essayé de contacter l’un de nos professeurs pour recevoir une aide personnalisée ? Excellente journée ! :)
J’aimerais bien avoir un prof de math
On peut rajouter, en géométrie analytique, les coefficients directeurs égaux et ,en géométrie vectorielle, les vecteurs directeurs et les vecteurs normaux respectivement colinéaires.