Chapitres
Voici un cours pratique sur les suites réalisé par des ambassadeurs Superprof qui ont lancé leur application de e-learning, Studeo : preview exclusive pour Superprof !
Il se décompose en deux temps :
- une vidéo de cours de 5 minutes pour comprendre les points clés,
- un exercice d'application et sa vidéo de correction pour maîtriser la méthode.
1) Limites de Suites : En l'infini - le cours en Terminale
Vidéo Antonin - Cours :
https://youtu.be/974UJKMoyGI
À retenir sur ce point de cours :
- Convergence vers un réel : Idée de couloir aussi petit qu'on veut - 1 Ça ne vient pas toujours se coller de manière propre !
On dit que la suite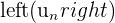 
tend vers un réel 
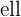quand 
tend vers 
, si tout intervalle ouvert contenant 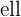contient tous les termes de la suite à partir d'un certain rang.
On dit que 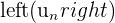converge et on note 
.
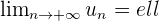- Divergence en et 
On dit que la suite 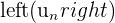tend vers quand tend vers , si pour tout réel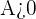 
, l'intervalle ]
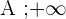[ contient tous les termes de la suite à partir d'un certain rang.
On dit que 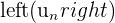diverge et on note 
.
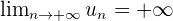On dit que la suite 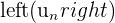tend vers quand tend vers , si pour tout réel 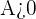, I'intervalle ] 
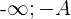[ contient tous les termes de la suite à partir d'un certain rang.
On dit que 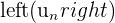diverge et on note 
.
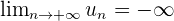- Points supplémentaires:
o Unicité de la limite
o On peut être divergent sans partir vers ou - 
2) Forme indéterminée 1 : factoriser par terme de plus haut degré - exercice d'application
Avant de voir la vidéo de correction ci-dessous, vous pouvez vous essayer à l'exercice d'application suivant :
Forme indéterminée 1 : factoriser par terme de plus haut degré
Déterminer la limite de la suite 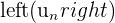suivante quand tend vers .
u_{n}=n^{2}-n
Vidéo Kevin - Application :
https://youtu.be/mNUg8djvsdk
3) Forme indéterminée 2 : la quantité conjuguée
Avant de voir la vidéo de correction ci-dessous, vous pouvez vous essayer à l'exercice d'application suivant :
Forme indéterminée : fonctions rationnelles
Déterminer la limite de la suite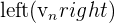 
suivante quand tend vers .
v_{n}=\frac{4 n^{2}}{n+1}
Vidéo Kevin - Application :
https://youtu.be/zZmAxnF1zF0
Vous pouvez également retrouver les pdf du superprof ici :
14
Pour retrouver ces vidéos, ainsi que de nombreuses autres ressources écrites de qualité, vous pouvez télécharger l'application Studeo (ici leur website) pour iOS par ici ou Android par là !
Résumer avec l'IA :
Vous avez aimé cet article ? Notez-le !
Loading...
Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !