Chapitres
Voici un cours pratique sur la continuité réalisé par des ambassadeurs Superprof qui ont lancé leur application de e-learning, Studeo : preview exclusive pour Superprof !
Il se décompose en deux temps :
- une vidéo de cours de 5 minutes pour comprendre les points clés,
- un exercice d'application et sa vidéo de correction pour maîtriser la méthode.

1) Lien avec l'étude des suites - le cours en Terminale
Vidéo Antonin - Cours :
https://youtu.be/hWDnlbd6P2A
À retenir sur ce point de cours :
Théorème du point fixe
Soit une fonction  définie et continue sur un intervalle
définie et continue sur un intervalle  et soit une suite
et soit une suite 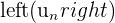 telle que pour tout
telle que pour tout  , on
, on 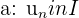 et
et 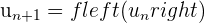 . Si
. Si 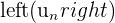 converge vers
converge vers  de
de  alors
alors 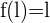 .
.
2) Prolongement par continuité - exercice d'application
Avant de voir la vidéo de correction ci-dessous, vous pouvez vous essayer à l'exercice d'application suivant :
Prolongement par continuité
Soit la fonction  définie sur
définie sur  par :
par :

left{\begin{array}{l}
f(x)=x sin \frac{1}{x} text { si } x neq 0 \
f(0)=0
\end{array}right.

1. Tracer sur une calculatrice la fonction  pour
pour  non nul. Que peut-on conjecturer sur la continuité de
non nul. Que peut-on conjecturer sur la continuité de  en 0 ?
en 0 ?
2. Démontrer cette conjecture.
Vidéo Kevin - Application :
https://youtu.be/FaW-6to4exs
Vous pouvez également retrouver le pdf du superprof ici :
PDF Continuité : Prolongement par continuité
Pour retrouver ces vidéos, ainsi que de nombreuses autres ressources écrites de qualité, vous pouvez télécharger l'application Studeo (ici leur website) pour iOS par ici ou Android par là !
Résumer avec l'IA :













Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !