Chapitres

Opération de deux nombres relatifs
Règle des signes
Propriété ( Règle des signes) :
Le PRODUIT de deux nombres relatifs de même signe est positif. Le PRODUIT de deux nombres de signes contraires est négatif.
| Produit | + | - |
|---|---|---|
| + | + | - |
| - | - | + |
Produit de deux nombres relatifs
Propriété : Pour multiplier deux nombres relatifs :
- 1. On applique la règle des signes
- 2. On multiplie les distances à zéro.
Exemples :
3,5 × (-2) = - (3,5 × 2) = -7
(-3) × (-4) = + (3 × 4) = 12.
Cas d'une division en écriture décimale
En cours de maths en ligne, on applique la règle des signes.
- Le quotient de deux nombres de même signe est positif.
−18,2÷−3,5=18,2÷3,5=5,2 - Le quotient de deux nombres de signes contraires est négatif.
18,2÷−3,5=-(18,2÷3,5)= −5,2
Cas d'une division en écriture fractionnaire
On transforme la division en une multiplication par l'inverse et on applique la règle des signes.
• 1er exemple :
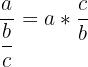
• 2e exemple :
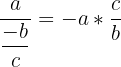
Règle des nombres relatifs
Pour multiplier ou diviser deux nombres relatifs la règle est la suivante :
La distance à zéro (ou valeur absolue) du résultat s'obtient en multipliant (ou divisant) les distances à zéro des deux nombres.
Le signe du résultat s'obtient grâce à la fameuse règles des signes :
PLUS par PLUS donne PLUS
PLUS par MOINS donne MOINS
MOINS par PLUS donne MOINS
MOINS par MOINS donne PLUS
'par' pour 'multiplié par' ou 'divisé par' : la règle des signes est la même pour les deux opérations.
Exemples :
(+ 3) x (- 5) = (- 15)
(+ 2,5) x (+ 3) = (+ 7,5)
(- 11) x (- 6) = (+ 66)
(- 42) ÷ (+ 7) = (- 6)
(- 21) ÷ (- 6) = (+ 3,5)
La multiplication des nombres relatifs doit conserver les propriétés connues de la multiplication et des nombres. Par exemple :
- (+ 2) x (+ 3) c'est la même chose que 2 x 3 : donc le résultat est 6, ou (+ 6).
- (+ 3) x (- 5) c'est la même chose que 3 x (- 5) = (- 5) + (- 5) + (- 5) = (- 15)
- La multiplication est commutative (on peut changer l'ordre) donc (- 5) x (+ 3) = (- 15)
Ainsi se justifient les trois premières lignes de la 'règle des signes' pour la multiplication. C'est un peu plus compliqué pour la multiplication de deux nombres négatifs.
Considérons le calcul :
A = (- 5) x [ (+ 3) + (- 3) ]
A = (- 5) x 0 parce que (+ 3) + (- 3) = 0 (somme de deux nombres opposés)
A = 0.
Mais comme la multiplication est distributive par rapport à l'addition, on a aussi
A = (- 5) x (+ 3) + (- 5) x (- 3)
donc A = (- 15) + (- 5) x (- 3)
En cours de maths seconde, comme on sait que le résultat est A = 0, on en déduit que (- 15) + (- 5) x (- 3) doit être égal à 0.
Pour cela il faut que (- 5) x (- 3) = (+ 15) (l'opposé de (- 15) )
Ainsi se justifie la dernière ligne de la règle des signes pour la multiplication.
La division
Une division donne le résultat d'une multiplication à trou :
(+8) ÷ (+2)= ? c'est comme ? x (+2) = (+8) ===>? = (+4), donc (+8) ÷ (+2) = (+4)
(-15) ÷ (+3)= ? c'est comme ? x (+3) = (-15) ===>? = (-5 ), donc (-15) ÷ (+3) = (-5)
(+24) ÷ (-6)= ? c'est comme ? x (-6) = (+24) ===>? = (-4), donc (+24) ÷ (-6) = (-4)
(-14) ÷ (-7)= ? c'est comme ? x (-7) = (-14) ===> ? = (+2), donc (-14) ÷ (-7) = (+2)
Où trouver des cours de maths pour réviser avant une épreuve ?
Produit d’un nombre relatif par (-1)
Remarque : Multiplier un nombre par (-1) revient à prendre l’opposé de ce nombre.
Exemples :
- 3,5 × (-1 ) = - (-3,5) = 3,5
(-1) × 1,2 = -1,2
(-1) × (-1) = - (-1) = 1.
Notation : l’opposé du nombre a se note – a.
Attention : - a peut être un nombre positif dans le cas où a est négatif. Exemple : - (-2,1) = 2,1
Carré d’un nombre relatif
Rappel : Le carré d’un nombre relatif a est le produit de ce nombre par lui-même.
Remarque : Le carré d’un nombre relatif est un nombre positif (d’après la règle des signes).
Exemples :
82 = 8 × 8 = 64 ; (-5)2 = (-5) × (-5) = 25
On notera qu'il n'est pas possible d'effectuer un calcul du carré d'un nombre relatif avec deux signes différents.
Opération de plusieurs nombres relatifs
Règle des signes « répétés »
Propriété (Règle des signes « répétés ») :
Un produit de nombres relatifs est positif s’il comporte un nombre pair de facteurs négatifs.
Un produit de nombres relatifs est négatif s’il comporte un nombre impair de facteurs négatifs.
Exemples :
−4 × −2,7 × 3 × −1,7 × −5,2 × 7 est un produit contenant quatre facteurs négatifs, donc ce produit est positif.
−2 × −5 × −4 × 3 est un produit contenant trois facteurs négatifs, donc ce produit est négatif.
Produit de plusieurs nombres relatifs
Propriété : Pour multiplier deux nombres relatifs :
- 1. On applique la règle des signes « répétée ».
- 2. On multiplie les distances à zéro.
Exemple : (-5) × (-2) × 3 × (-7) = – (5 × 2 × 3 × 7) = - 210.
Division de nombres relatifs
Le quotient de a par b, noté a / b est le nombre relatif qui, multiplié par b, donne a.
Exemple :
(- 35) / 5 est le nombre qui, multiplié par 5, est égal à (- 35).
Or, (-7) × 5 = - 35. On en déduit que (- 35) / 5 = = - 7.
Règle des signes
Propriété:
Le QUOTIENT de deux nombres relatifs de même signe est positif. Le QUOTIENT de deux nombres de signes contraires est négatif.
Pour diviser deux nombres relatifs :
- On applique la règle des signes
- On divise les distances à zéro.
Exercices
Exercice 1 : Divisions assistées
Pour calculer les quotients donnés, compléter en utilisant les expressions proposées : "de même signe" ; "de signes contraires" ; "positif" ; "négatif" ; "quotient".
a) Calcul de 12 / (-4) : Les deux nombres sont .............................. dont le quotient est ..................... . J'en déduit que : 12 / (-4) = -3.
b) Calcul de (-9) / (-18) : Les deux nombres sont ........................... donc le quotient est ...................... . J'en déduis que : (- 9) / (- 18) = 0,5.
c) Calcul de (-45) / 15 : Les deux nombres sont ............................ donc le quotient est ...................... .J'en déduis que : -45 / 15 = -34.
Exercice 2 : Divisions
Calculer sans poser les opérations :
12 / (-4) ; -36 / (-9) ; -9 / 2 ; -14,6 / (-2) ; 0 / (-4) ; 9,3 / (-3)
Exercice 3 : Signes de quotients plus complexes
Détermine le signe des quotients donnés.
a) Calcul de (12 x (-2)) / ((-4) x (-8)) Le numérateur 12 x (-2) comporte.....facteur(s) négatif(s) donc il est ............ Le dénominateur -4 x (-8) comporte .... facteur(s) négatif(s) donc il est ...... Le numérateur et le dénominateur de ce quotient sont de signes .................. donc le quotient est ........................ .
b) Calcule de (1 x (-2) x 3) / (4 x (-7)) Le numérateur 1 x (-2) x 3 comporte ....... facteur(s) négatif(s) donc il est ................ . Le dénominateur 4 x (-7) comporte .......... facteur(s) négatif(s) donc il est ............... . Le numérateur et le dénominateur de ce quotient sont de .................. signes donc le quotient est ........................ .
c) Calcul de : - (-2,1) / (-12) x (-4,2) Le numérateur - (-2,1) comporte ....... facteur(s) négatif(s) donc il est ............... . Le dénominateur (-12) x (-4,2) comporte .......... facteur(s) négatif(s) donc il est ............... . Le numérateur et le dénominateur de ce quotient sont de .................. signes donc le quotient est ........................ .
Corrigés
Exercice 1 :
a) Calcul de 12 / (-4) : Les deux nombres sont 12 et -4 dont le quotient est -3 . J'en déduit que : 12 / (-4) = -3.
b) Calcul de (-9) / (-18) : Les deux nombres sont -9 et -18 donc le quotient est 1/2 . J'en déduis que : (- 9) / (- 18) = 0,5.
c) Calcul de (-45) / 15 : Les deux nombres sont -45 et 15 donc le quotient est -3 . J'en déduis que : -45 / 15 = -34.
Exercice 2 :
12 / (-4) = -3
-36 / (-9) = 4
-9 / 2 = -4,5
-14,6 / (-2) = 7,3
0 / (-4) = 0
9,3 / (-3) = -3,1
Exercice 3 :
a) Calcul de (12 x (-2)) / ((-4) x (-8)) Le numérateur 12 x (-2) comporte 1 facteur négatif donc il est négatif. Le dénominateur -4 x (-8) comporte 2 facteurs négatifs donc il est positif. Le numérateur et le dénominateur de ce quotient sont de signes opposés donc le quotient est négatif.
b) Calcule de (1 x (-2) x 3) / (4 x (-7)) Le numérateur 1 x (-2) x 3 comporte 1 facteur négatif donc il est négatif. Le dénominateur 4 x (-7) comporte 1 facteur négatif donc il est négatif . Le numérateur et le dénominateur de ce quotient sont de mêmes signes donc le quotient est positif.
c) Calcul de : - (-2,1) / ((-12) x (-4,2)) Le numérateur - (-2,1) comporte 2 facteurs négatifs donc il est positif. Le dénominateur (-12) x (-4,2) comporte 2 facteurs négatifs donc il est positif. Le numérateur et le dénominateur de ce quotient sont de mêmes signes donc le quotient est positif.
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !