Chapitres

Introduction
Les droites remarquables au sein d'un triangle sont nombreuses. Ces dernières permettent de nombreux travaux sur les triangles et aident dans de nombreuses démonstrations. C'est pourquoi il est très utile et très important de les connaître.
Si deux droites sont parallèles à une même troisième, elles sont parallèles entre elles.
Si deux droites sont perpendiculaires à une même troisième, alors elles sont parallèles entre elles.
Si une droite est perpendiculaire à une droite parallèle à une autre, certaines propriétés se déduisent.
Les triangles : définitions et propriétés essentielles

Ce tableau récapitule les différentes droites remarquables d'un triangle que nous allons détailler ensuite :
| Droite remarquable | Définition | Convergence |
|---|---|---|
| Hauteur | Passe par un sommet et est perpendiculaire au côté opposé | Converge au point orthocentre |
| Médiane | Relie un sommet au milieu du côté opposé | Converge au centre de gravité |
| Bissectrice | Coupe un angle en deux angles égaux | Converge au centre du cercle inscrit |
| Médiatrice | Perpendiculaire à un côté et passe par son milieu | Converge au centre du cercle circonscrit |
Définition d’un triangle
Le triangle se définit comme une figure plane dotée de trois côtés et trois angles. Ses trois angles sont nommés sommets et les trois segments qui relient ces sommets se nomment les côtés.
Propriétés importantes des triangles
- La somme des angles d'un triangle est égale à 180° ;
- Dans un triangle, la droite passant par les milieux de deux côtés opposés est parallèle au troisième côté et mesure la moitié de celui-ci ;
- Dans un triangle ABC isocèle en A, la médiane, la hauteur, la bissectrice issues de A et la médiatrice de la base [BC] sont confondues ;
- Dans un triangle ABC équilatéral, la médiane, la hauteur, la bissectrice issues d'un sommet et la médiatrice du côté opposé sont confondues et donc l'orthocentre, le centre de gravité, le centre du cercle circonscrit et le centre du cercle inscrit sont confondus ;
- Dans un triangle rectangle, la médiane relative à l'hypoténuse mesure la moitié de l'hypoténuse ;
- Dans un triangle rectangle, le cercle circonscrit à un triangle rectangle a pour diamètre l'hypoténuse, le centre du cercle circonscrit à un triangle rectangle est le milieu de l'hypoténuse ;
- Dans un triangle rectangle, les angles aigus sont complémentaires car leur somme est de 90°.
Les différents types de triangles
Il existe plusieurs types de triangles. Chacun d'entre eux dispose de caractéristiques particulières.
Le triangle plat
Le triangle plat est un triangle dont les sommets sont alignés. Visuellement, il ressemble à une droite.
Le triangle isocèle
Le triangle isocèle est un triangle qui dispose d'au moins deux côtés de même taille, ce qui fait que les deux angles adjacents à ce côté sont de même mesure. Dans un triangle isocèle, la médiatrice, la hauteur, la médiane et la bissectrice issues du sommet principal sont confondues. Par exemple, dans le triangle ABC isocèle en A, la droite issue de A joue simultanément le rôle de médiatrice, hauteur, médiane et bissectrice.
Le triangle équilatéral
Le triangle équilatéral est un triangle particulier dans lequel tous les côtés sont de même longueur. Il en résulte que tous ses angles soient de 60° puisque la somme des angles d'un triangle est de 180°.
Le triangle rectangle
Un triangle rectangle est un triangle dont l'un des angles mesure 90° et est donc un angle droit. Le côté opposé à cet angle droit est appelé l'hypoténuse. Les deux autres côtés sont les cathètes.
Le triangle obtusangle
Un triangle obtusangle est un triangle dont un angle est supérieur à 90° et les deux autres inférieurs à 90°.
Le triangle acutangle
Le triangle acutangle est un triangle dont aucun des trois angles ne mesure plus de 90°.
Les grands théorèmes des triangles
De nombreux théorèmes existent afin de calculer les mesures des côtés d'un triangle ou encore les mesures des angles de ces derniers. On y retrouve par exemple les célèbres théorèmes de Pythagore et théorèmes de Thalès.
Le théorème de Pythagore

Énoncé du théorème de Pythagore
Pythagore a énoncé dans son théorème la phrase suivante :
Dans un triangle rectangle, le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.
Explication du théorème

Cela signifie que pour un triangle ABC rectangle en A : AB² + AC² = BC².
Utilité du théorème de Pythagore
Le théorème de Pythagore est très fréquemment utilisé afin de pouvoir démontrer qu'un triangle est rectangle ou ne l'est pas. On utilise pour cela la réciproque et la contraposée du théorème de Pythagore :
Si AB² = AC² + BC² alors le triangle ABC est rectangle en A. Si AB² n’est pas égal à AC² + BC² alors le triangle n’est pas rectangle en C.
Comment demander de l'aide en cours de maths en ligne ?
Le théorème de Thalès
Thalès de Milet, mathématicien grec du VIᵉ siècle avant J.-C., est célèbre pour ses travaux sur la géométrie et les proportions.
Son théorème permet de calculer des longueurs dans des triangles lorsqu’une droite est parallèle à l’un des côtés.
Énoncé du théorème de Thalès
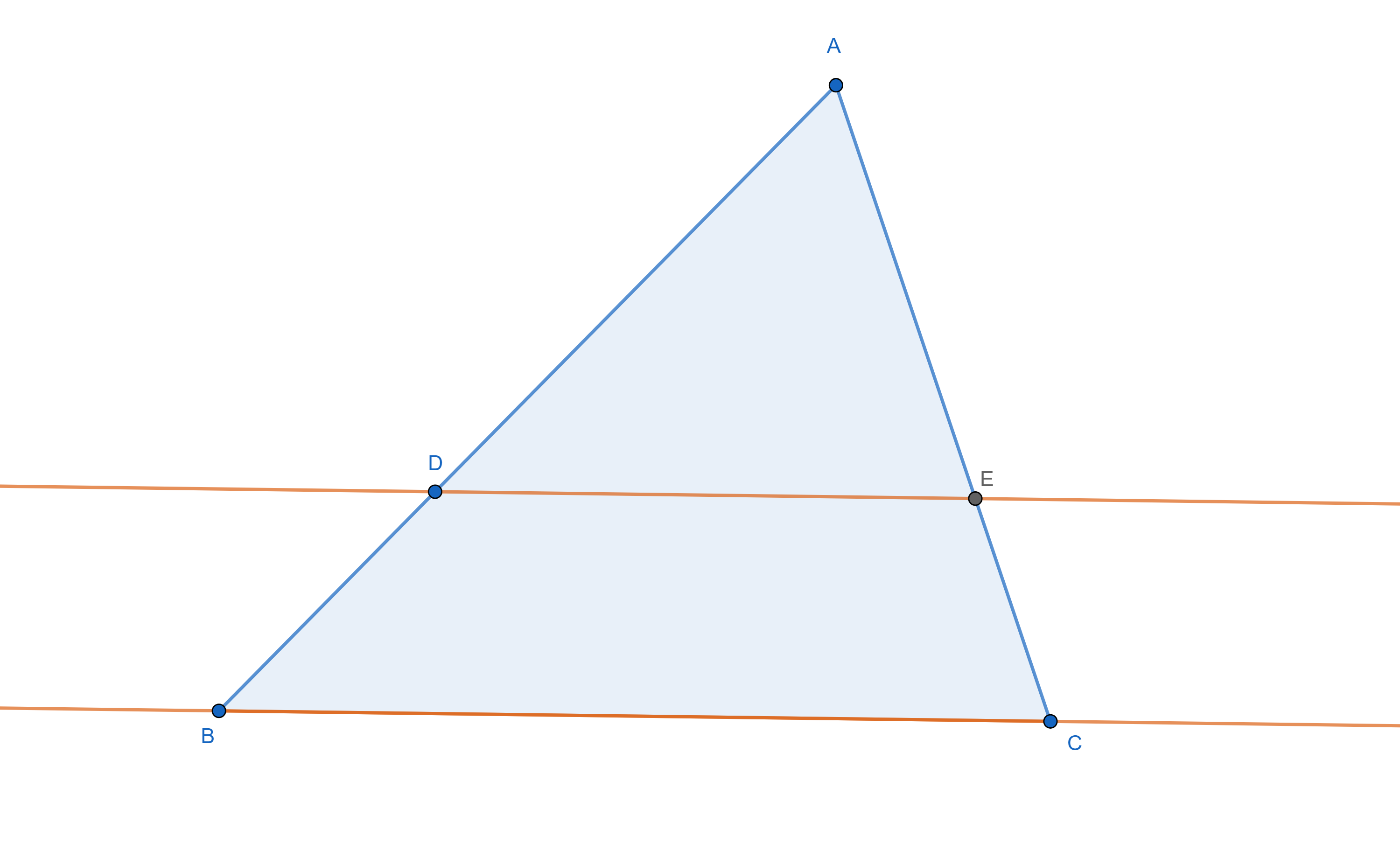
Dans un triangle ABC, si le point D est sur la droite (AB) et le point E sur la droite (AC) et que (DE) et (BC) sont parallèles, alors : 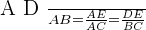
Utilité du théorème de Thalès
Le théorème de Thalès permet de faire des calculs sur les triangles. Il en découle d'autres théorèmes ou règles, tel que le théorème de la droite des milieux. Il stipule la phrase suivante :
Si un segment joint les milieux de deux côtés d’un triangle, alors il est parallèle au troisième côté, et sa longueur est égale à la moitié de celle de ce troisième côté.
La réciproque est aussi souvent utilisée : Dans un triangle ABC, soient les points D et E appartenant respectivement aux segments [AB] et [AC],
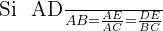
sont égaux, alors les droites (DE) et (BC) sont parallèles.
Les médiatrices des côtés d’un triangle
Définition d'une médiatrice
On appelle médiatrice d'un segment la droite perpendiculaire à ce segment et passant par le milieu de ce segment.
Propriétés des médiatrices
- Les médiatrices d'un triangle sont toujours concourantes ;
- Leur point d'intersection est le centre du cercle circonscrit ;
- La médiatrice d'un segment est l'ensemble de points équidistant des extrémités du segment.
Les médianes d'un triangle
Définition d'une médiane
Une médiane est une droite dans un triangle passant par un sommet de celui-ci et par le milieu du côté opposé à ce sommet.
Propriétés des médianes
- Les trois médianes d'un triangle sont concourantes ;
- Le point d'intersection des 3 médianes est appelé le centre de gravité du triangle ;
- Le point d'intersection des 3 médianes est situé à 2 / 3 de leur longueur en partant du sommet.
Les hauteurs d’un triangle
Définition d’une hauteur
Une hauteur est une droite dans un triangle passant par un sommet et perpendiculaire au côté opposé.
Propriétés des hauteurs
- Les trois hauteurs d'un triangle sont concourantes ;
- Le point d'intersection des 3 hauteurs est appelé l'orthocentre du triangle ;
- Quand le triangle a 3 angles aigus l'orthocentre est à l'intérieur du triangle, quand le triangle a un angle obtus l'orthocentre est à l'extérieur du triangle.
Les bissectrices d’un triangle
Définition d’une bissectrice
La bissectrice d'un angle est la demi-droite issue du sommet d'un triangle, qui partage l'angle en 2 angles de même mesure.
Propriétés des bissectrices
- Les trois bissectrices d'un triangle sont concourantes ;
- Le point d'intersection des 3 bissectrices est appelé le centre du cercle tangent aux 3 côtés du triangle, également connu sous le nom de cercle inscrit au triangle ;
- Ce centre du cercle inscrit au triangle se trouve toujours dans le triangle.
Exercices sur les droites remarquables d’un triangle
Pour s'entraîner et bien reconnaître les différentes droites remarquables, voici quelques exercices :
Complétez les phrases avec le type de droite remarquable correspondant. Vous pouvez vous aider d'un schéma à main levée.
Données :
Le triangle ABC est un triangle quelconque.
D est le milieu du segment [AB].
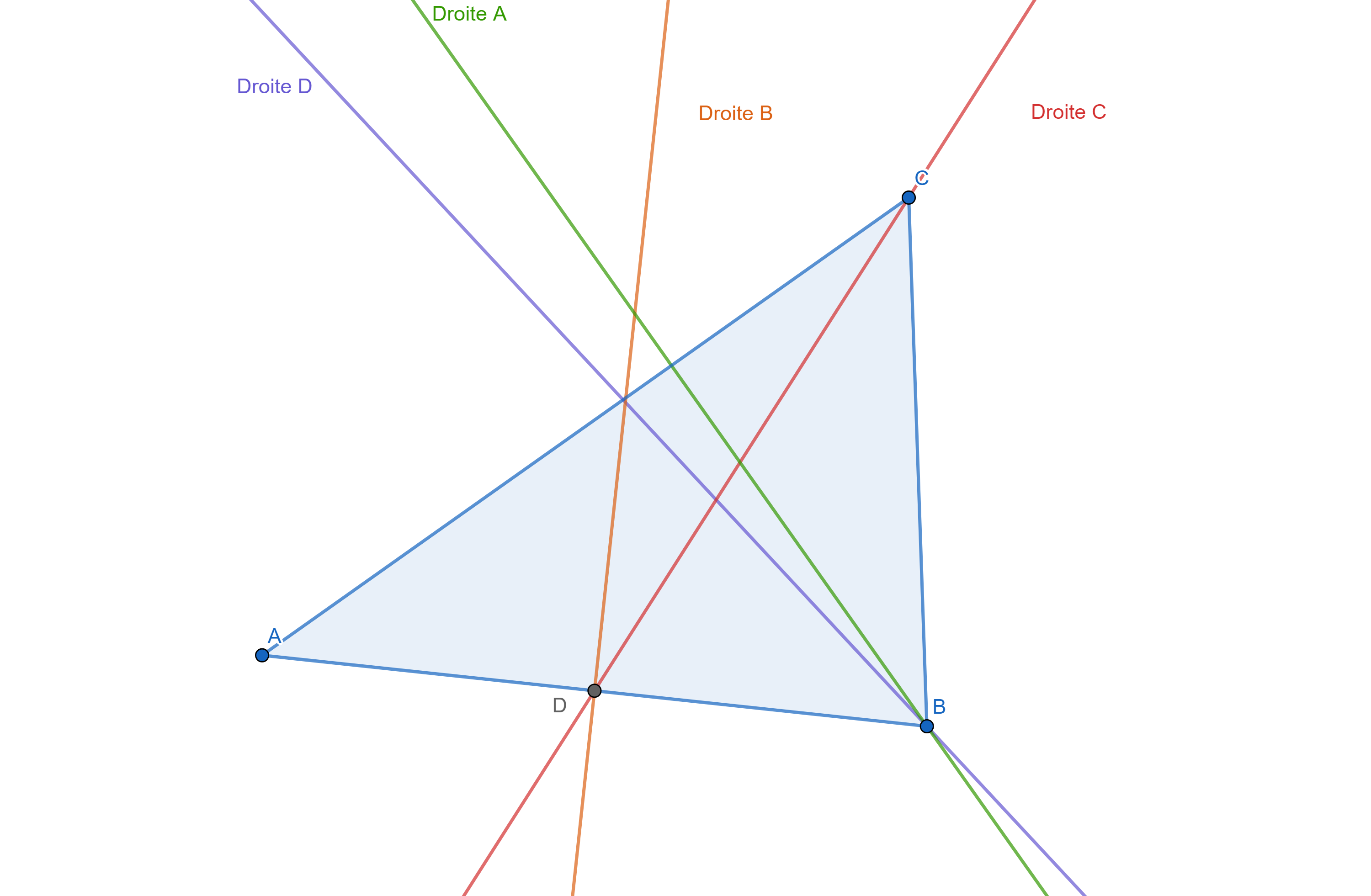
La droite A est une ______ du triangle ABC.
Ce champ est requis.
La droite A est une hauteur du triangle ABC.
La droite B est une ______ du triangle ABC.
Ce champ est requis.
La droite B est une médiane du triangle ABC.
La droite C est une ______ du triangle ABC.
Ce champ est requis.
La droite C est une bissectrice du triangle ABC.
La droite D est une ______ du triangle ABC.
Ce champ est requis.
La droite D est une médiatrice du segment [AB], donc une médiatrice du triangle ABC.
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !