Chapitres
- 01. Histoire du calcul littéral
- 02. Introduction géométrique
- 03. Conventions d'écriture
- 04. Le calcul littéral : la distributivité
- 05. Double distributivité dans le calcul littéral
- 06. L’expression littérale
- 07. Identités remarquables
- 08. Les équations
- 09. Réduction d'une expression littérale
- 10. Développer en utilisant la distributivité
- 11. Suppression de parenthèses
- 12. Développeravec la double distributivité
- 13. Exercice d'entraînement sur le calcul littéral
L'expression « calcul littéral » signifie « calcul avec des lettres ». Le calcul littéral englobe de nombreuses équations et inéquations mathématiques. Il est parfois difficile de s'y retrouver mais il est essentiel de bien comprendre le détail de tous ces calculs car ils constituent les bases des calculs mathématiques à un niveau supérieur.
Les expressions littérales permettent aussi de traduire des problèmes ou des formules en équations ou fonctions.


Histoire du calcul littéral
Le calcul littéral (calcul avec des lettres) également appelé calcul algébrique, est un outil développé par l’un des plus grands mathématiciens français François Viète. Ce dernier a attribué une lettre à des quantités et des coefficients inconnus dans des calculs.
François Viète (1540-1603) est avocat au parlement de Paris. Sa profession lui laissant peu de temps pour étudier les sciences, il se consacre alors aux mathématiques pour le plaisir, domaine qu’il considère comme un loisir.
C’est en 1571 qu’il publie son premier ouvrage sur la trigonométrie « Canon mathematicus ». Il y présente de nombreuses formules de cosinus et sinus qui permettent de simplifier les calculs, ainsi que des tables trigonométriques.
En 1580, Viète est nommé conseiller privé d’Henri IV. Il est chargé de décrypter les messages secrets interceptés que les Espagnols s’envoient. Réussissant systématiquement à les décrypter, il provoque l’exaspération de ses ennemis qui finissent par l’accuser de sorcellerie et veulent le dénoncer au pape. Pour se défendre de ses accusateurs, Viète publiera alors sa méthode dans un traité en 1590.
En 1591, il publie un deuxième ouvrage « In artem analyticem isagoge » qui représente une avancée considérable pour l’algèbre. Pour Viète, le calcul littéral a pour but principal de résoudre tout problème. Les grandeurs recherchées sont donc désignées par des voyelles et les grandeurs connues par des consonnes.

Introduction géométrique
Pour découvrir les différentes formules de distributivité, calculons de deux manières l’aire du rectangle ACDF.

Rappel : aire d’un triangle = côté x longueur
Aire(ACDF) = AF × AC = k × (a + b). Ou Aire(ACDF) = Aire(ABEF) + Aire(BCDE) = AF × AB + AF × BC = k × a + k × b. On a donc : k × (a + b) = k × a + k × b.
Conventions d'écriture
- Par convention on peut supprimer le signe "x" (fois) entre :
- un nombre et une lettre : 5 x a = 5a
- un nombre et une parenthèse : 3 x (x + 1) = 3(x + 1)
- une lettre et une parenthèse : a x (3x + 5) = a(3x + 5)
- deux lettres : a x b = ab
- deux parenthèses : (4x + 7) x (2x + 5) = (4x + 7) (2x + 5)
- D'après les propriétés de la multiplication :
- 1 x b = b
- 0 x a = 0
Le calcul littéral : la distributivité
Le calcul littéral est un calcul avec des nombres et des lettres où chaque lettre désigne une inconnue (nombre qu’on ne connait pas, dont on ne sait pas la valeur). Voici la formule de base du calcul littéral : ka+kb = k(a+b) ou (a+b)k.
Décomposons cette formule : k × (a + b) = k × a + k × b ; soit k(a + b) = ka + kb
C’est le même principe pour la soustraction : k × (a − b) = k × a − k × b ; soit k(a − b) = ka – kb
On appelle cela la distributivité car on « distribue les lettres (nombres dans un cas concret) sur les autres ». Dans un autre langage on dit qu’on développe l’expression.
Développer signifie transformer un produit en somme ou différence. Factoriser signifie transformer une somme ou différence en produit.
3x² + 6x = 3x(x + 2)
7a² − a = a(7a − 1)
Développement du calcul littéral
Développer signifie transformer une multiplication en une somme ou en une différence.
Dans les formules précédentes, on a transformé le produit de k par (a + b) (ou (a −b)) en une somme (ou une différence). Ici, on dit que l’on a développé k × (a + b) et k × (a − b). On parle alors de distributivité de la multiplication par rapport à l’addition (quand il y a le signe positif) ou à la soustraction (quand il y a le signe négatif).
Exemple : développer l’expression 5(2x − 8). D’après les formules de distributivité, on a : 5(2x − 8) = 5 × 2x − 5 × 8 = 10x – 40.
Factorisation de l'expression littérale
À l’inverse, factoriser signifie transformer une somme ou une différence en un produit. En lisant de droite vers la gauche les formules de distributivité précédentes, on dit que l’on a factorisé l’expression par k (produit de deux facteurs). On a donc factorisé k × a + k × b et k × a − k × b.
La factorisation permet de simplifier l’expression mathématique. Factoriser une expression c’est trouver un facteur commun aux nombres situés entre les parenthèses.
Exemple : Factorisons par x l’expression 2x + 7x. 2x + 7x = x (2 + 7) = 9x.
Simplifions maintenant en factorisant l’expression 6a + 4b – 2a + 8b. 6a + 4b – 2a + 8b = 6a – 2a + 4b + 8b = a(6 – 2) + b(4 + 8) = 4a + 12b
Double distributivité dans le calcul littéral
La double distributivité s’apparente à appliquer la distributivité simple deux fois. On applique la double distributivité pour développer ce type d’expression : (a + b) (c + d) tel que a, b, c et d sont des nombres relatifs (nombres entiers positifs ou négatifs).
Cette technique consiste à distribuer « a » sur « c » et « d » ; et « b » distribué sur « c » et « d ». Autrement dit, on multiplie « a » par « c » puis par « d » et on multiplie « b » par « c » puis « d ».
La formule est la suivante : (a + b) (c + d) = ac + ad + bc + bd.
Détaillons un peu plus cette formule : (a + b) (c + d) = a x c + a x d + b x c + b x d = ac + ad + bc + bd Ce sera la même chose pour la soustraction : (a + b) (c – d) = a x c + a x (-d) + b x c + b x (-d) = ac – ad + bc – bd.
Attention aux signes négatifs lors de la multiplication !
(a – b) (c – d) = a x c + a x (-d) + (-b) x c + (-b) x (-d) = ac + (-ad) + (-bc) + bd = ac – ad – bc + bd.
Lorsqu’on multiplie un chiffre positif avec un chiffre négatif le résultat est négatif. Ex : 2 x (-3) = -6
Lorsqu’on multiplie deux chiffres négatifs entre eux, le résultat est positif. Ex : (-4) x (-5) = 20
On peut donc supprimer les parenthèses à l’intérieur de l’expression et directement mettre le signe correct.
(2x + 3)(−x + 4) = −2x² + 8x − 3x + 12 = −2x² + 5x + 12
(3x − 1)² = 9x² − 6x + 1
L’expression littérale
Une expression littérale est une expression contenant une ou plusieurs lettres, comme nous venons de le voir. Ces lettres pouvant varier, on dit que ce sont des variables. Par exemple, A = 7a + 4b – 3 est une expression littérale.
Dans une expression littérale, on peut supprimer le signe « multiplier » lorsqu’il est placé :
- Devant ou derrière une lettre
- Devant ou derrière une parenthèse
- Entre deux lettres ou deux parenthèses
De plus, pour simplifier une expression littérale et donc faciliter le calcul, on peut modifier l’ordre des facteurs dans cette expression.
A = 10 x a x 6 = 10 x 6 x a = 60 x a = 60a
Ordonner une expression
Il est primordial d’ordonner une expression composée d’additions et/ou de soustractions. Pour cela, il faut placer les termes dans l’ordre décroissant des exposants des variables qui apparaissent dans l’expression. La lettre ayant la puissance la plus forte se placera en première position et ainsi de suite. On ordonne l’expression selon les puissances les plus hautes au moins hautes.
Voici l’expression littérale B = 12 + 6x2 – 4x + x3
Pour rendre cette expression plus « juste » et plus lisible, il faut l’écrire sous cette forme : B = x3 + 6x2 – 4x + 12
Dans une expression littérale où le signe « – » précède une parenthèse, il faut réécrire tous les termes à l’intérieur de cette parenthèse en changeant leur signe. On réécrit alors le signe contraire au signe initialement présent dans la parenthèse.
Ex : C = (2x2 + 4x2 + x2) – (6x + 8x – 3)
C = 7x2 – (14x – 3) = 7x2 – 14x + 3
Pour une explication plus mathématique, il faut retenir que la multiplication d’un nombre positif avec un nombre négatif a pour résultat un nombre négatif. Et la multiplication d’un nombre négatif avec un nombre négatif a pour résultat un nombre positif.
On place les termes de plus haut degré à gauche jusqu’au plus petit degré à droite.
Identités remarquables
Les identités remarquables sont très utiles pour développer ou factoriser rapidement des expressions littérales. Il faut connaitre ces identités dans les deux sens.
Carré d’une somme
(a+b)2 = a2 + 2 x a x b + b2
Donc (a+b)2 = a2 + 2ab + b2
Carré d’une différence
(a-b)2 = a2 – 2 x a x b + b2
Donc (a-b)2 = a2 – 2ab + b2
Produit de la somme par la différence
(a+b)(a-b) = a x a + a x (-b) + b x a + b x (-b) = a2 – ab + ab – (b)2
Donc (a+b)(a-b) = a2 – b2
Tableau récapitulatif des identités remarquables
| Formule générale | Exemple concret | Explication |
|---|---|---|
| (a + b)² = a² + 2ab + b² | (x + 3)² = x² + 6x + 9 | Carré d’une somme : multiplie chaque terme et additionne les résultats |
| (a − b)² = a² − 2ab + b² | (x − 4)² = x² − 8x + 16 | Carré d’une différence : multiplie chaque terme et applique le signe moins correctement |
| (a + b)(a − b) = a² − b² | (x + 5)(x − 5) = x² − 25 | Produit de la somme par la différence : on obtient la différence des carrés |
| (a + b + c)² = a² + b² + c² + 2ab + 2ac + 2bc | (x + 2 + y)² = x² + 4 + y² + 4x + 4y + 4xy | Carré d’une somme à trois termes : multiplie chaque terme entre eux et additionne |
| (a − b − c)² = a² + b² + c² − 2ab − 2ac + 2bc | (x − 2 − y)² = x² + 4 + y² − 4x − 4y + 4xy | Carré d’une différence à trois termes : attention aux signes négatifs |
| (a + b)(a + c) = a² + ac + ab + bc | (x + 2)(x + 3) = x² + 3x + 2x + 6 = x² + 5x + 6 | Produit de deux binômes : applique la distributivité deux fois |
Les équations
Équation du premier degré à une inconnue
On appelle équation du premier degré à une inconnue toute équation qui peut s'écrire sous la forme ax + b = cx + d où a, b, c et d sont des nombres tels que a ≠ b. Ce type d’équation admet une unique solution.
Pour résoudre une équation du premier degré à une inconnue on peut : • Ajouter ou soustraire un même nombre aux deux membres de l'équation. • Multiplier ou diviser les deux membres de l'équation par un même nombre non nul.
Exemple : résoudre l'équation 8x – 3 = 6x + 5
- On soustrait 6x à chaque membre
- Puis on ajoute 3 à chaque membre
- Et enfin, on divise par 2 chaque membre
8x – 3 = 6x + 5
Premièrement, 8x – 3 – 6x = 6x + 5 – 6x
2x – 3 = 5
Deuxièmement, 2x – 3 + 3 = 5 + 3
2x = 8
Troisièmement, 2x/2 = 8/2
X = 4
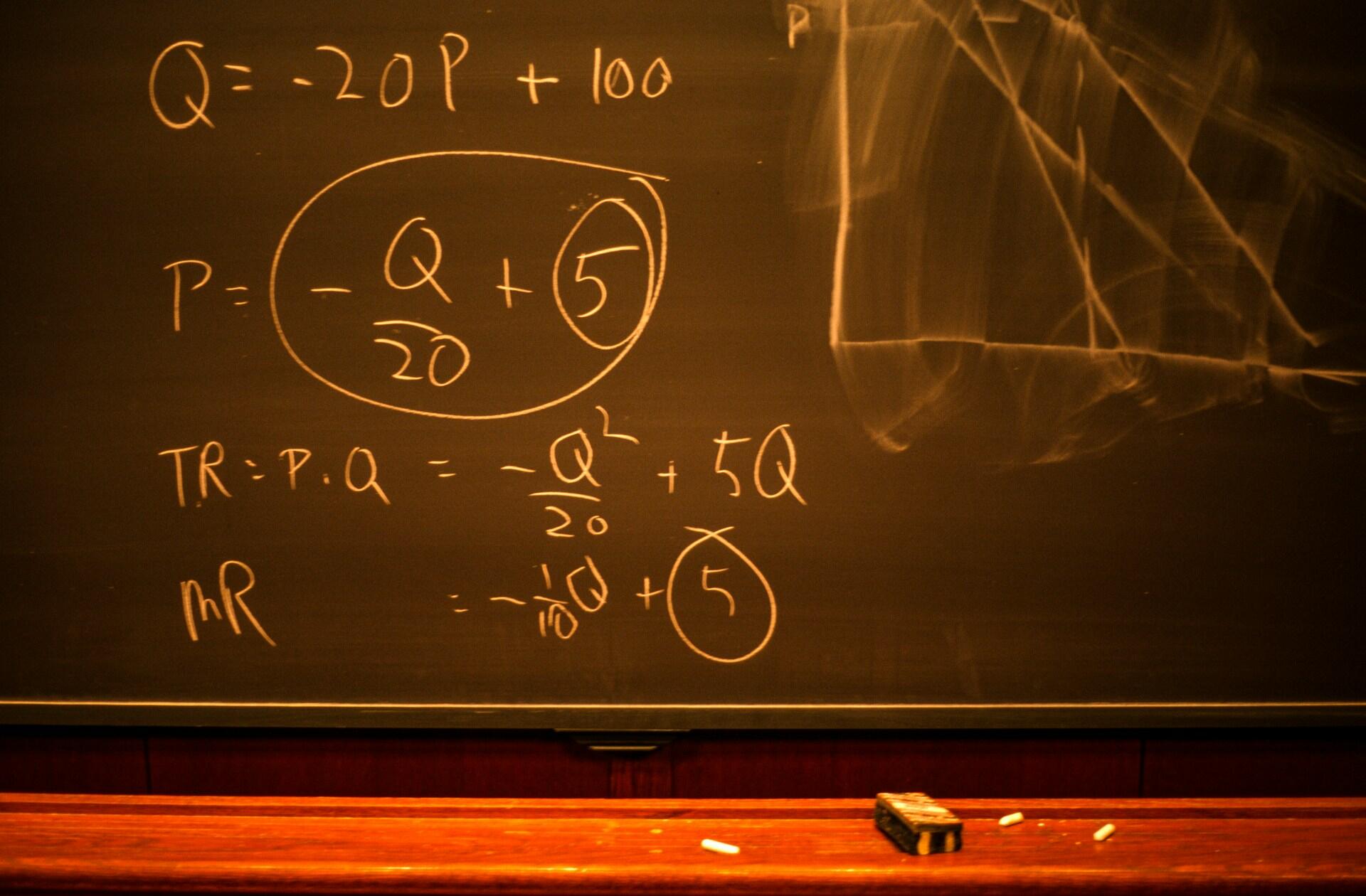
Équation du second degré
Une équation du second degré prend la forme ax²+bx+c=0 (avec a non nul). Pour résoudre une équation du second degré, il faut calculer le discriminant delta Δ. Pour calculer le discriminant il suffit d'appliquer cette formule : Δ = b2 – 4ac. Ensuite selon le résultat, on va pouvoir trouver, s’il y en a, le nombre de solutions.
Si Δ < 0 : il n’y a aucune solution.
Ou alors, si Δ = 0 : il y a une seule solution à l’équation qu’on calculera avec x = -b/2a
Et si Δ > 0 : il y a deux solutions à l’équation qu’on calculera avec x1 = (-b+√Δ)/(2a) et x2 = (-b - √Δ)/(2a).
Réduction d'une expression littérale
Réduire une expression littérale signifie écrire cette expression sous forme plus simple.
Exemple : 5y + 8y = 13y (5 + 8) y = 8y
4z² + 3z² = 7z²
- Par contre 4 + 5y et 4x - 7x² ne peuvent pas se réduire.
4w x 2 = 8w
3y x 9y = 27y²
Développer en utilisant la distributivité
Développer c'est transformer un produit en somme.
Quels que soient les nombres a, b et c :
Exemple : Développer.
A = 2 (2x + 4) B = x (5x - 3)
A = 2 x 2x + 2 x 4 B = x x 5x - x x 3
A = 4x + 8 B = 5x² - 3x
Suppression de parenthèses
Addition et parenthèses
Lorsque les parenthèses sont précédées du signe "+" et qu'elles ne sont pas suivies du signe "x" ou ":", on peut supprimer les parenthèses.
Exemple : Réduire
2x + (3x + 4) = 2x + 3x + 4 = 5x + 4
4 + (-5 + 3y) = 4 + (-5) + 3y = -1 + 3y
Soustraction et parenthèses
Quels que soient les nombres relatifs a et b :
Cette propriété permet de gérer les parenthèses précédés un signe "-".
Exemple : Réduire
3x - (5 - 7x) = 3x - 1 x (5 - 7x) = 3x - 5 + 7x = 10x - 5
Développeravec la double distributivité
Quels que soient les nombres relatifs a, b, c et d :
Exemple : Développer et réduire
A = (2x + 5) (x + 3) = 2x² + 6x + 5x + 15
= 2x² + 11x + 15
Exercice d'entraînement sur le calcul littéral
Nous allons maintenant voir si vous avez bien compris la leçon ! Pour cela, un petit exercice :
Soit l’expression littérale suivante : Questions : Expression de départ Développement avec distributivité Réduction de l'expression Factorisation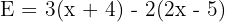
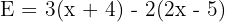
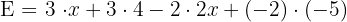
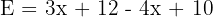
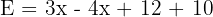
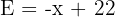
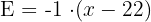
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Merci c’est parfait pour les révisions du brevet
Interesting
Demain j’ai un contrôle sur le calcul littéral j’ai besoin de technique et d’exercice , pouvez vous m’expliquer des choses importantes a savoir .
Je suis en 5ème et j’ai du mal à faire le calcul littéral parfois
Bonjour ! Pas toujours évident effectivement, de s’atteler à ce genre d’exercice. Mais en pratiquant, en s’entraînant, et en faisant des petits exercices en dehors des cours, vous finirez par y arriver ! Si ça n’est toujours pas le cas, vous pouvez évidemment revenir vers nous et prendre un cours avec l’un de nos professeur de maths, qui se fera une joie de vous aider !
Bonne journée