Chapitres
Dans le vaste univers des mathématiques, nous sommes constamment confrontés à des nombres qui ne tombent pas "juste". Que ce soit le résultat d'une division infinie comme 10 divisé par 3 (3,333...), ou des constantes irrationnelles célèbres comme le nombre Pi (π), nous avons souvent besoin de simplifier ces valeurs pour les rendre manipulables et intelligibles.
Pour ce faire, deux techniques principales s'offrent à nous : l'arrondi et la troncature. Si l'arrondi est souvent le réflexe premier enseigné à l'école, la troncature est tout aussi fondamentale, notamment en troncature maths, en informatique et en analyse de données.
La troncature consiste à supprimer les chiffres après une certaine décimale, sans effectuer d’arrondi. Par exemple, 5,678 tronqué au dixième donne 5,6. Très présente en calcul numérique, programmation et analyse de données, la troncature permet de gagner en clarté et en efficacité.

Dans ce guide complet, nous allons explorer en détail la troncature d'un nombre, ses méthodes, ses différences cruciales avec l'arrondi et ses applications concrètes. Prêt à couper court aux décimales superflues ? C'est parti.

Qu’est-ce que la troncature ?
Avant de manier le "ciseau" mathématique, il est essentiel de comprendre précisément ce que signifie tronquer un nombre et pourquoi cette opération, qui semble brutale de prime abord, est d'une utilité redoutable.
Troncature : définition
Si l'on cherche une troncature def (définition) simple, on pourrait dire qu'il s'agit de l'action de couper une partie d'un nombre pour en réduire la précision. Étymologiquement, le mot vient du latin truncare, qui signifie "couper" ou "mutiler" (comme on tronque un arbre de ses branches).
En mathématiques, effectuer la troncature d'un nombre décimal signifie supprimer purement et simplement tous les chiffres situés après un certain rang donné (l'unité, le dixième, le centième, etc.). Contrairement à l'arrondi, on ne se soucie absolument pas de la valeur du chiffre qui suit la coupure.
Exemple concret : Prenons le nombre 12,897.
Si l'on fait un arrondi à l'unité, on regarde le chiffre après la virgule (8). Comme 8 est supérieur ou égal à 5, on arrondit à l'entier supérieur : 13.
Si l'on effectue une troncature à l'unité, on coupe tout ce qui dépasse après la virgule. On garde uniquement la partie entière. Le résultat est : 12.
La troncature maths est donc une approximation par défaut (pour les nombres positifs). C'est une méthode "aveugle" : elle ne cherche pas à être le plus proche possible de la valeur réelle, mais à respecter un format strict.
Pourquoi utilise-t-on la troncature ?
Pourquoi choisir une méthode moins précise que l'arrondi ? La troncature sert dans différents domaines où la rapidité ou la structure de la donnée prime sur la précision absolue.
En calcul numérique Lorsqu'on effectue des calculs mentaux rapides ou que l'on souhaite estimer un ordre de grandeur, la troncature est souvent plus rapide. Elle permet de limiter le nombre de décimales pour simplifier les calculs intermédiaires. De plus, dans certaines approximations contrôlées (comme l'encadrement d'une racine carrée), on utilise la troncature pour donner la borne inférieure de l'intervalle.
En programmation et informatique C'est sans doute le domaine où la troncature est la plus utilisée. La gestion des nombres flottants (les nombres à virgule en informatique) est complexe. La troncature automatique se produit souvent lors de la conversion d'un type de variable "décimal" (float) vers un type "entier" (integer). Par exemple, si vous codez un logiciel qui compte le nombre de personnes pouvant entrer dans des voitures de 4 places et que vous avez 13 personnes, le calcul 13/4 donne 3,25. Une troncature à l'unité donne 3 : il y aura 3 voitures pleines (la 4ème voiture incomplète ne compte pas comme "pleine"). L'ordinateur utilise cette opération pour l'optimisation de performances dans des scripts mathématiques.
En statistiques et finance La troncature de données est utilisée pour nettoyer des bases de données en supprimant les valeurs extrêmes ou le "bruit" insignifiant après la virgule (les millièmes de centimes n'existent pas physiquement). Dans le domaine bancaire, certaines règles d'intérêts se basent sur des troncatures strictes pour ne jamais verser plus que le montant calculé au centime près.
Pour approfondir vos connaissances sur la manipulation des nombres, vous pouvez consulter nos ressources sur les nombres décimaux qui expliquent en détail la structure de ces valeurs.
Les différentes méthodes de troncature
La technique reste la même (couper), mais l'endroit où l'on place le ciseau change le résultat. Voici les trois niveaux de troncature les plus courants que vous rencontrerez au collège et au lycée.
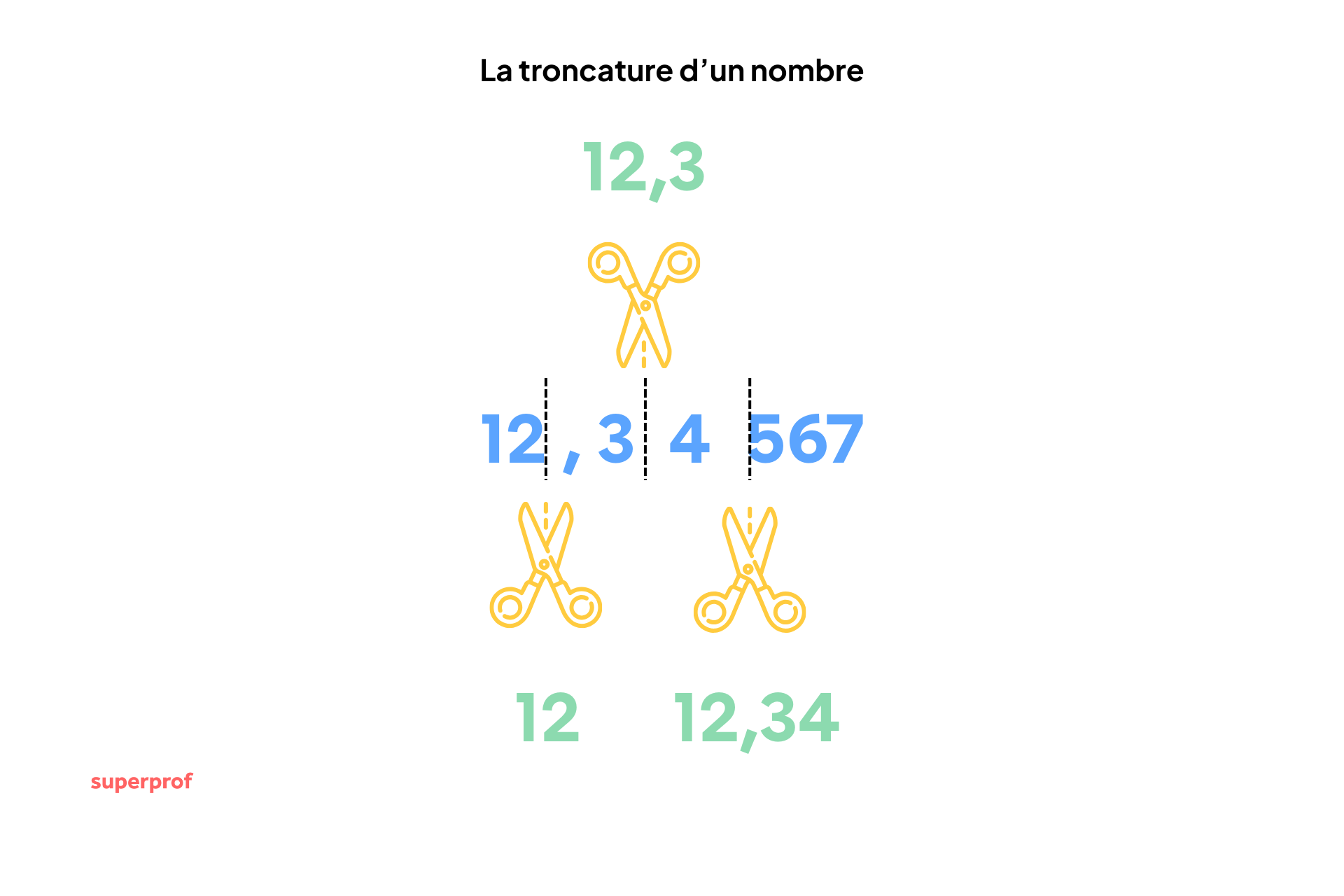
Troncature à l’unité
La troncature à l’unité est la forme la plus radicale. Elle consiste à ne garder que la partie entière du nombre. On supprime tout ce qui se trouve après la virgule.
Exemples :
- 7,93 tronqué à l'unité → 7
- 0,999 tronqué à l'unité → 0 (Attention, c'est ici que la différence avec l'arrondi, qui donnerait 1, est la plus flagrante).
- 154,2 tronqué à l'unité → 154
Cette méthode est utilisée dans les calculs simples où les fractions n'ont pas d'importance (compter des objets entiers) ou en programmation pour récupérer l'index d'un tableau.
Troncature au dixième
La troncature au dixième signifie que l'on conserve un seul chiffre après la virgule. C'est une précision souvent suffisante pour noter des moyennes scolaires ou des températures.
Pour réaliser une troncature au dixième, on regarde le premier chiffre après la virgule, on le garde, et on efface tout le reste.
Exemples :
- 8,79 → 8,7 (Même si 8,79 est très proche de 8,8, la troncature l'ignore).
- 3,14159 (π) → 3,1
- 12,09 → 12,0
C'est un cas fréquent en données arrondies au rang supérieur pour simplifier la lecture de graphiques ou de tableaux de bord.
Troncature au centième ou millième
Plus on avance dans les décimales, plus la précision augmente. La troncature au centième (2 chiffres après la virgule) ou au millième (3 chiffres après la virgule) est plus utilisée en physique, finances ou statistiques.
Troncature au centième : Ex. : 3,4567 → 3,45
C'est le standard pour les prix en euros (bien que l'arrondi soit légalement préféré pour le total, les prix unitaires intermédiaires sont parfois tronqués dans les bases de données).
Troncature au millième : Ex. : 3,4567 → 3,456
Utilisée par exemple pour les taux de change ou les mesures de précision en chimie.
Les erreurs de troncature
Si la troncature est pratique, elle n'est pas sans danger mathématique. En coupant une partie du nombre, on crée un décalage avec la réalité. C'est ce qu'on appelle l'erreur de troncature.

Qu’est-ce qu’une erreur de troncature ?
L'erreur de troncature correspond à la perte d’information due à la suppression des décimales. Mathématiquement, c'est la différence entre la valeur exacte (x) et la valeur tronquée (tronc(x)).
Par exemple, si vous tronquez 10,9 à l'unité, vous obtenez 10.
L'erreur est de 10,9 - 10 = 0,9.
C'est une erreur presque aussi grande que l'unité elle-même ! Contrairement à l'arrondi où l'erreur maximale est de 0,5 (la moitié de l'unité), l'erreur de troncature peut aller jusqu'à 0,999...
Conséquences possibles
Dans un calcul unique, cette erreur peut sembler négligeable. Mais les conséquences deviennent graves si les erreurs sont cumulées.
Résultats faussés : Si vous additionnez 1000 nombres tronqués, vous cumulez 1000 fois la petite erreur. Au final, la somme sera significativement inférieure à la réalité.
Erreurs d’analyse : En sciences, tronquer trop tôt les mesures peut cacher des phénomènes subtils qui se jouent au niveau des décimales (variations infimes de température, de concentration, etc.).
Erreurs significatives en calcul itératif : En informatique, dans des boucles de calculs répétitifs, l'erreur de troncature peut faire diverger un algorithme complet. C'est un problème classique en analyse numérique.
Comment limiter ces erreurs ?
Pour éviter ces pièges, deux règles d'or s'appliquent :
- Ne tronquer qu’en fin de calcul : Il ne faut jamais tronquer (ni arrondir) en cours d’opération. Gardez la précision maximale de votre calculatrice ou ordinateur tout au long des étapes, et n'appliquez la troncature que sur le résultat final pour l'affichage.
- Travailler avec des marges de tolérance : Si vous utilisez des valeurs tronquées, soyez conscient que votre résultat est une approximation par défaut (inférieure à la réalité) et indiquez-le (en utilisant le signe ≃ par exemple).
Troncature et arrondi : quelles différences ?
C'est la confusion la plus fréquente chez les élèves. Troncature et arrondi sont deux méthodes d'approximation, mais leur logique est différente. Il est crucial de savoir distinguer quand appliquer l'une ou l'autre.
Comparaison entre une troncature et un arrondi
La règle à retenir est simple :
- Troncature = Suppression directe. On coupe, sans réfléchir.
- Arrondi = Ajustement. On regarde le chiffre suivant pour décider si l'on reste au niveau actuel ou si l'on monte au niveau supérieur.
Pour mieux comprendre, prenons un exemple comparatif avec le nombre 5,8 :
| Méthode | Action | Résultat pour 5,8 |
|---|---|---|
| Troncature à l'unité | On garde le chiffre des unités (5) et on jette le reste (,8) | 5 |
| Arrondi à l'unité | On regarde le dixième (8). Comme 8 ≥ 5, on monte à l'unité supérieure. | 6 |
Si le chiffre des dixièmes est inférieur à 5 (par exemple 5,2), la troncature et l'arrondi donneront le même résultat (5). La différence n'apparaît que lorsque les décimales sont élevées (5, 6, 7, 8, 9).
Quand utiliser l’un ou l’autre ?
Utilisez la troncature (ou valeur approchée par défaut) : Pour un calcul simplifié rapide, une estimation brute de tête, ou lorsque le contexte exige de ne pas dépasser une certaine valeur (par exemple, si vous avez 19,90€, vous ne pouvez acheter que pour 19€ d'objets à 1€, pas 20).
Pour obtenir le résultat final le plus proche de la vérité. C'est la méthode privilégiée en physique, en chimie et dans la vie quotidienne pour les prix (arrondi au centime le plus proche) car elle minimise l'erreur statistique moyenne.
Troncature : exercices pratiques
Rien de tel que la pratique pour maîtriser la troncature maths. Essayez de résoudre ces exercices avant de regarder les corrections.
Exercice 1 : Troncature simple
Tronquez les nombres suivants à l'unité :
14,23
Ce champ est requis.
27,99
Ce champ est requis.
0,56
Ce champ est requis.
100,01
Ce champ est requis.
Exercice 2 : Troncature vs Arrondi
Pour le nombre 16,748, donnez :
La troncature au dixième
Ce champ est requis.
L'arrondi au dixième
Ce champ est requis.
Troncature au centième
Ce champ est requis.
Arrondi au centième
Ce champ est requis.
Pour continuer votre apprentissage des approximations et de la précision des nombres, n'hésitez pas à explorer notre cours sur les chiffres significatifs, très utile en sciences physiques.
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
j’ai un teste sur arrondir un nombre le 13/10/25 pouvez vous m’aider
Je voudrais faire les cours de maths et merci pour la trocanture mes je voudrais que vous me montre la trocanture de 17/2 et4,69/5
Bonjour ! Venez découvrir comment nos formateurs passionnés chez Superprof peuvent enrichir votre apprentissage avec un soutien sur mesure. J’espère que vous passerez une journée aussi agréable que fructueuse ! :)
Svp on a demandé à ma fille ceci : quel est la troncature de 3,25 au centième à l’excès en sachant que c le résultat de 26/8
Merci d’avance
BONJOUR MONSIEUR
j,aimerai l,arrondi du nombre 5,12543
Je voudrais faire les cours de maths et merci pour la trocanture mes je voudrais que vous me montre la trocanture de 17/2 et4,69/5
Bonjour,
L’arrondi de ce chiffre est 5,1 ou 5,13.
Bonne journée !
Bonjour monsieur.
J’aimerai connaître l’arrondi dunombre 0,000345002. Svp
Bonjour,
L’arrondi de ce chiffre est 0,1 ou 0,0004 si vous souhaitez être plus précis.
Bonne journée !