
Cours d’Algèbre : le Calcul Littéral
Règles de calculs des expressions algébriques I) Rappels 1°/ Réduction d'une expression A = 3x - 5x - 8x + x A = x (3 - 5 - 8 + 1) A = -9x B = -12x² + 5x - 1 + 3x² - 3x + 4 B = -9x² + 2x + 3 2°/[…]
20 mai 2007 ∙ 1 minute de lecture

Rappels de Mathématiques : Nombres et Opérations
Notions de calcul et d'algèbre à l'usage des 3ème I) Règles de calcul 1°/ Règle des signes pour la multiplication et la division Le produit de 2 relatifs de même signe est positif. Le produit de 2 relatifs de signe différent est négatif. 2°/ Dans un calcul, l'ordre de priorité des opérations est le suivant[…]
20 mai 2007 ∙ 2 minutes de lecture

Exercice et Corrigé : les Pourcentages
Calculer les hausses et baisses des valeurs Calculer le prix d'un article de 45€ après une hausse de 3% 45x3/100=1,35 l'augmentation est 1,35€ 45+1,35=46,35 Le nouveau prix est 46,35€ Calculer le prix d'un article de 45€ après une baisse de 3% 45x3/100=1,35 la baisse est 1,35€ 45-1,35=43,65 Le nouveau prix est 43,65€ Remarques: gagnons du[…]
28 avril 2007 ∙ 1 minute de lecture

Équations, Inéquations et Problèmes
Cours de Mathématiques en Troisième CONTENU Équations et inéquations du premier degré. Ordre et multiplication. Inéquation du premier degré à 1 inconnue. Résolutions de problèmes du premier degré ou s'y ramenant. COMPÉTENCES EXIGIBLES Utiliser le fait que des nombres relatifs de la forme ab et ac sont dans le même ordre que b et c[…]
26 avril 2007 ∙ 2 minutes de lecture
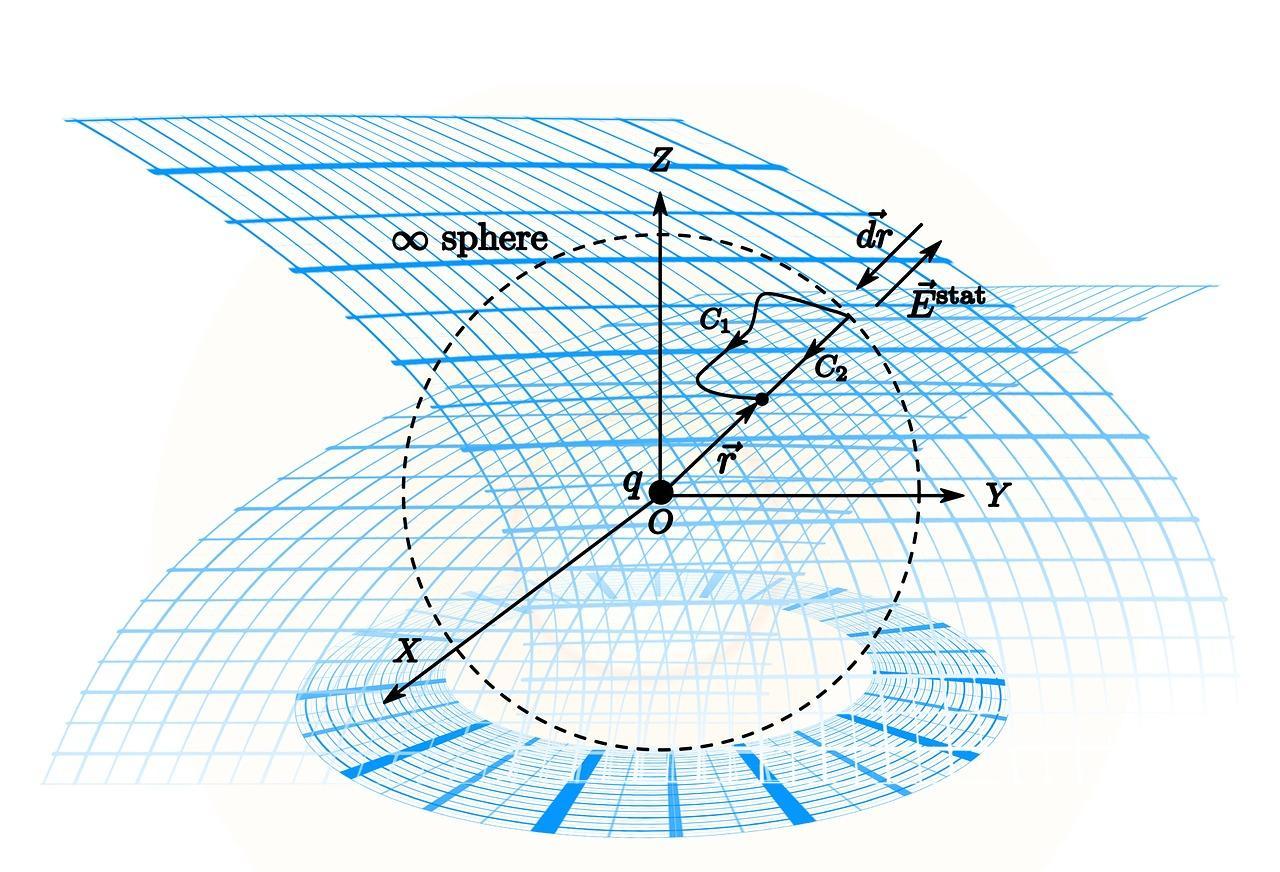
Grandes Notions de Trigonométrie en Troisième
Cosinus, sinus et tangente au programme CONTENUS Triangle rectangle : relations trigonométriques COMPÉTENCES EXIGIBLES Connaître et utiliser dans le triangle rectangle des relations entre le cosinus, le sinus ou la tangente d'un angle aigu et les longueurs de 2 côtés du triangle. Utiliser la calculatrice pour déterminer des valeurs approchées : du sinus, du cosinus[…]
26 avril 2007 ∙ 1 minute de lecture

Cours de 3ème : Racines Carrées et Opérations
Calculs élémentaires sur les radicaux CONTENUS Calculs élémentaires sur les radicaux (racines carrées). Racine carrée d'un nombre positif. roduit et quotient de 2 radicaux. COMPÉTENCES EXIGIBLES Savoir que , si a désigne un nombre positif, est le nombre positif dont le carré est a. Sur des exemples numériques où a est un nombre positif, utiliser[…]
26 avril 2007 ∙ 2 minutes de lecture
Géométrie de l’Espace en Troisième
Calculs géométriques sur toutes les figures CONTENUS Géométrie dans l'espace . Sphère Problèmes de sections planes de solides. Calculs d'aires et de volumes. COMPÉTENCES EXIGIBLES Savoir que la section d'une sphère par un plan est un cercle. Savoir placer le centre de ce cercle et calculer son rayon connaissant le rayon de la sphère et[…]
26 avril 2007 ∙ 3 minutes de lecture

Cours de Mathématiques : l’Arithmétique
Les règles arithmétiques de base I. RAPPELS : LES ENSEMBLES DE NOMBRES 1) Les entiers naturels : Ce sont les nombres que l'on peut compter sur ses doigts. ex : 0 ; 1 ; 2 ... 2) Les entiers relatifs : Ce sont les entiers naturels et leurs opposés. ex : ... ; -3 ;[…]
26 avril 2007 ∙ 2 minutes de lecture

Fiche d’Exercices de Géométrie en Troisième
Entraînements géométriques et trigonométriques Exercice 1 Tracer deux droites d et d' perpendiculaires en O, puis marquer un point I tel que I n'appartienne ni à d, ni à d'. 1. Construire le symétrique A de O par rapport à I. 2. a) Construire le symétrique de la droite d par rapport au point I[…]
1 avril 2007 ∙ 1 minute de lecture

Résumé : les Volumes et les Aires
Les calculs des surfaces des figures géométriques Sphère, Boule Aire : 4 x 3,14 x R² Volume : 4/3 x 3,14 x R³ 3,14 = pie R = rayon Cube Aire : 6c² Volume : c³ Pavé droit Aire : 2(Lh + lh + Ll) Volume : L x l x h L =[…]
14 mars 2007 ∙ 1 minute de lecture

Solutions : Exercices Types du Brevet de Maths
Correction des questions de l'examen de calcul ACTIVITES NUMERIQUES Ex 1 : a) D = 9x² - 25 + 3x² - 6x + 5x - 10 = 12x² - x - 35 b) 9x² - 25 = (3x)² - 5² = (3x + 5)(3x -5) D = (3x + 5)(3x -5) + (3x +5)(x -2) = (3x +5)[(3x -5)[…]
14 mars 2007 ∙ 3 minutes de lecture

Entraînement au Brevet de Mathématiques
Questions-types de l'épreuve de maths l'emploi de la calulatrice est autorisé. ACTIVITES NUMERIQUES ex 1: On donne l'expression : D = 9x² - 25 + (3x + 5)(x - 2) a) Développer D b) Factoriser 9x² - 25, puis factoriser D. c) Calculer D pour x = V3 * d) Résoudre l'équation (3x +5)(4x -[…]
14 mars 2007 ∙ 2 minutes de lecture

Exercice d’Algèbre de Type Brevet
Entraînements aux questions de l'examen Exercice On considère l'expression suivante : A = ( x√3 + 1 )2 - ( 2x - 7)( 1 + x√3 ) + 5 + 5x√3 1. Développer, réduire et ordonner A. 2. Factoriser au maximum A. 3. Résoudre A = 0. Solutions 1. A = ( x√3 + 1[…]
1 mars 2007 ∙ 1 minute de lecture

Exercice de Mathématiques : Écriture Scientifique
Factoriser les expressions suivantes Donne l'écriture scientifique des nombres suivant : ( calculatrice ommise ) A = 0,000276354 = ..... B = 9352000 = ..... C = 25 x 103 x ( 2 x 102 )2 = ..... D = 0,0024 x 106 x 1,25 x 10-5 = ..... Solutions : A = 0,000276354 =[…]
1 mars 2007 ∙ 1 minute de lecture

Problème de Géométrie Posé par Thalès
Une question que se pose le savant grec Exercice Lorsque Thalès vit la pyramide de Chéops, il fut émerveillé. Il voulut en connaître la hauteut. Il mesura d'abord le côté de la base carré : il trouva 227 m. Il se plaça ensuite au milieu d'un côté de la base carré et il séloigna de[…]
27 février 2007 ∙ 1 minute de lecture

Problème de Mathématiques avec Système
Déduire le système de calcul de l'énoncé Exercice Une usine fabrique deux sortes d'objets : A et B. L'objet A nécessite 2,4 kg d'acier et 3 heures de fabrication. L'objet B nécessité 4 kg d'acier et 2 heures de fabrication. Combien d'objet de chaque sortes a-t-on fabriqué en 67 heures de travail et en utilisant[…]
27 février 2007 ∙ 1 minute de lecture

La Factorisation en Arithmétique
Factoriser une expression mathématique Pour factoriser, il faut déja repéré le facteur commun ( un facteur commun c'est un facteur présent dans toutes les expressions ex: (2x + 1) (3 - x) -2(4x - 3) (3 - x) Ici, il y a deux expressions alors on doit trouver deux fois un même facteur (facteur commun), il[…]
14 janvier 2007 ∙ 2 minutes de lecture

PGCD : Définition et Utilisation
Le Plus Grand Commun Diviseur de deux nombres PGCD de deux nombres entiers Parmis tous les diviseurs communs à deux nombres entiers a et b, il y en a un qui est plus grand que tous les autres: c'est le Plus Grand Commun Diviseur à a et b. On le note: PGCD(a;b) ou PGCD(b;a) exemple:[…]
10 janvier 2007 ∙ 1 minute de lecture

La Trigonométrie : Principes de Base
L'étude des triangles rectangles D'où vient le mot "trigonométrie" ? Trigonométrie vient du grec ancien τρίγωνος (prononcé "trigonos"), "triangulaire" et μέτρον (prononcé "métron"), "mesure". On considère un triangle ABC rectangle en A : Dans les triangles rectangles • L'hypoténuse est le plus grand côté du triangle. • Le côté adjacent à un angle est le[…]
9 janvier 2007 ∙ 3 minutes de lecture

Résumé : le Plus Grand Commun Diviseur
Les principes du PGCD en mathématiques a, b, k¹0 sont des nombres entiers naturels. 1) Diviseurs d'un entier Quand est un entier naturel, k est un diviseur de a. On dit aussi que a est un multiple de k ou encore que a est divisible par k. 6 est un diviseur de 18 ; 3[…]
9 janvier 2007 ∙ 2 minutes de lecture

Étude de Géométrie dans l’Espace
Analyse de figures géométriques en 3D 1) Cube, parallélépipède La section d'un cube ou d'un parallélépipède par un plan parallèle à une face est un carré ou un rectangle ayant les mêmes dimensions que cette face. La section d'un cube ou d'un parallélépipède par un plan parallèle à une arête est un rectangle. 2) Cylindre[…]
9 janvier 2007 ∙ 2 minutes de lecture

Cours de Maths : les Vecteurs et les Coordonnées
La construction géométrique par fonction 1) Composition de deux translations 2) Somme de deux vecteurs méthode du triangle : Soit A, B et C trois points quelconques, on dit que la somme des vecteurs et est le vecteur . Cette règle est la relation de Chasles : Relation de Chasles : Les points se suivent[…]
8 janvier 2007 ∙ 1 minute de lecture
Cours de Mathématiques : les Équations
Les expressions à variables : usages et résolutions a, b, c, d, x et y sont des nombres relatifs. 1) Rappels 3´12+5=41 est une égalité ; 3x+5=41 est une équation qui n'est vraie que pour x=12 ; on dit que 12 est la solution de l'équation. Résoudre une équation c'est trouver la valeur qu'il faut[…]
8 janvier 2007 ∙ 2 minutes de lecture

Les Grands Principes de la Trigonométrie
L'étude des triangles rectangles La trigonométrie s'applique dans les triangles rectangles. 1) Le théorème de Pythagore et sa réciproque Dans un triangle rectangle, le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés. Réciproquement, si dans un triangle le carré du plus grand côté est égal à la somme des[…]
8 janvier 2007 ∙ 2 minutes de lecture

La Propriété de Thalès dans le Triangle
Résumé : le théorème de Thalès 1) Rappels Si deux droites sont perpendiculaires à une même troisième alors elles sont parallèles entre elles. Si deux droites sont parallèles avec un point commun alors elles sont confondues. 2) Les situations de Thalès d et d' sont deux droites sécantes en A et les droites (BC) et[…]
8 janvier 2007 ∙ 2 minutes de lecture

Révisions de Mathématiques en Troisième
Les grandes notions vues cette année I/pGcD a/algorithme d'euclide Le pgcd c'est simple !! Imaginé que vous avez cette question : determiné le pgcd de 12 et 18 : Donc je vous explique vous prené le plus grand nombre et vous faite ceci regardé! 18=12x......+......(puis avec votre calculatrice vous faite:18:r12ca vous fai 1 6 apré vous faite:[…]
7 janvier 2007 ∙ 1 minute de lecture

Exercices d’Entraînement au Brevet de Maths
Problèmes de mathématiques de l'épreuve I Activité numérique Exercice 1 Soit D = (2x+3)² + (2x+3)(7x-2) 1 . Développer et réduire D. 2. Factoriser D. 3. Calculer D pour x= -4 4. Résoudre l'équation: (2x+3)(9x+1)=0 Exercice 2 Pierre a gagné 84 sucettes et 147 bonbons à un jeu. Etant très généreux, et ayant surout très peur du dentiste,[…]
1 janvier 2007 ∙ 3 minutes de lecture

Réponses : Exercices de Factorisation
Factoriser les équations proposées A = 3x + 3 A = 3(x + 1) B = (x + 1)(x + 5) + 7(x + 1) B = (x + 1)((x + 5) + 7) B = (x + 1)(x + 5 + 7) B = (x + 1)(x + 12) C = (x + 1)(3x[…]
19 décembre 2006 ∙ 2 minutes de lecture

Exercices de Maths : Calculs Numériques
Entraînement aux opérations algébriques exercice 1 alain bernard et charlotte decident de faire chacun une question del'exercice suivant A=5/4 - 2/3 *9/16 B=16*10^-5*3*10^4 / 24*10^-3 C=V63+2V7-5V28 (V==>racine carrée) 1.calculer A et donner le resultat sous la forme d'une fraction irreductible 2.calculer B et donner le resultat sous forme d'un nombre entier 3.ecrire C sous la[…]
18 décembre 2006 ∙ 1 minute de lecture
