Chapitres

Les ensembles de nombres
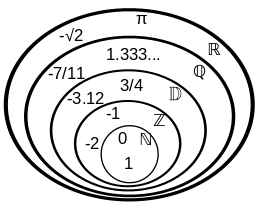
On distingue dans les différentes opérations élémentaires, à savoir l'addition, la soustraction, la multiplication et la division, différents types de nombres. En effet, il existe différents ensembles de nombres. Ces ensembles sont inclusifs, c'est à dire que chaque ensemble est compris dans le suivant. Ainsi dans les ensemble de nombres, on a du plus petit au plus grand :
- Les nombres entiers positifs. Ce sont les nombres les plus intuitifs à savoir ceux qui sont utilisés dans la vie de tous les jours : 1,2,3.... On dit que cet ensemble de nombres appartient à ℕ.
- Les nombres entiers négatifs. Ils représentent l'opposé des nombres entiers positifs. Ce sont tous les nombres entiers ayant le signe moins devant : -1,-2,-3. On dit que cet ensemble de nombres appartient à ℤ. Pour information, on dit que l'opposé d'un nombre est son égal négatif (l'opposé de 1 est -1). En revanche, lorsque l'on parle de l'inverse, il s'agit de sa fraction (l'inverse de 2 est 1/2).
- Les nombres entiers décimaux. Ils représentent l'ensemble des nombres avec une virgule mais qui sont finis. Par exemple 4,5 est un nombre décimal. En revanche 0,3333333... n'est pas un nombre décimal car il n'a pas de nombres finis après la virgule. On note cet ensemble de nombre ⅅ.
- Les nombres rationnels. Il s'agit de l'ensemble des nombres qui peuvent s'écrire sous forme de fraction. A noter que les fractions donnant des résultats finis, à l'instar de 3/4 = 0,75 appartiennent également aux nombres entiers décimaux. On note cet ensemble de nombre ℚ.
- Les nombres réels. Ils comprennent l'ensemble des nombres qui ne sont pas finis et dont l'ensemble décimal est non périodique. On peut noter des nombres réels notables tels que π, √2... On note cet ensemble de nombre ℝ.
Remarque : Il existe encore un autre ensemble de nombres appelé les complexes. Ce dernier ensemble de nombres sera étudié dans les classes supérieures.
Exercice
Pour chacun des nombres suivants, déterminer à quel ensemble de nombres ils appartiennent :
Corrigé
 est un nombre entier positif. Il appartient à ℕ.
est un nombre entier positif. Il appartient à ℕ.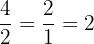 . Etant un nombre entier positif, il appartient à ℕ.
. Etant un nombre entier positif, il appartient à ℕ.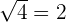 . Etant un nombre entier positif, il appartient à ℕ.
. Etant un nombre entier positif, il appartient à ℕ.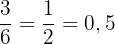 . Il s'agit d'un nombre décimal fini qui appartient par conséquent à ⅅ.
. Il s'agit d'un nombre décimal fini qui appartient par conséquent à ⅅ. . Il s'agit d'un nombre décimal fini négatif. Il appartient donc à ⅅ.
. Il s'agit d'un nombre décimal fini négatif. Il appartient donc à ⅅ.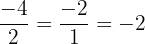 . Il s'agit d'un nombre entier négatif et appartient par conséquent à ℤ.
. Il s'agit d'un nombre entier négatif et appartient par conséquent à ℤ.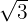 donne un résultat infini de décimales et non périodique. Il appartient à ℝ.
donne un résultat infini de décimales et non périodique. Il appartient à ℝ. est un nombre avec des décimales infinies mais périodiques. Il appartient donc à ℚ.
est un nombre avec des décimales infinies mais périodiques. Il appartient donc à ℚ.
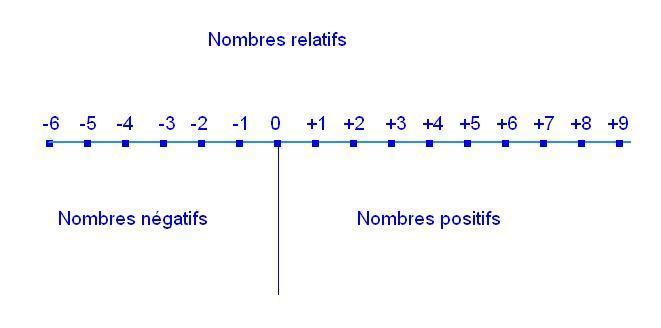
Produit des nombres relatifs
Concernant les différents produits entre des nombres de signe positif et négatif, on obtient les résultats suivants via la règle des signes :
- Le produit de deux nombres relatifs de même signe est positif
- Le produit de deux nombres relatifs de signes différents est négatif
Par ailleurs, en généralisant la règle des signes :
- Le produit de n nombres relatifs dont le nombre n de facteur négatif est pair est positif
- Le produit de n nombres relatifs dont le nombre n de facteur négatif est impair est négatif

Exercice
En cours de math, pour chacune des opérations suivantes, déterminer si le résultat est positif ou négatif:
- (-3)*(-1)
- 2*(-1)
- (-1)*(-1)*(-1)
- (-2)*(-2)*2
- (-2)*2*(-2)
- (-2)*(-2)*(2)*(-1)*2*(-1)
- (-2)*2*(-1)*2*(-1)*1*2*(-1)
Corrigé
- (-3)*(-1) : Il s'agit d'un produit de deux nombres relatifs de même signe. Le signe du résultat est donc positif.
- 2*(-1) : Il s'agit d'un produit de deux nombres relatifs de signes différents. Le signe du résultat est donc négatif.
- (-1)*(-1)*(-1) : Le nombre de nombres relatifs de facteur négatif est égal à 3 est par conséquent est impair. Le signe du résultat est négatif.
- (-2)*(-2)*2 : Le nombre de nombres relatifs de facteur négatif est égal à 2 est par conséquent est pair. Le signe du résultat est positif.
- (-2)*2*(-2) : Malgré un ordre différent, le nombre de nombres relatifs de facteur négatif est égal à 2 est par conséquent est pair. Le signe du résultat est positif.
- (-2)*(-2)*(2)*(-1)*2*(-1) : Le nombre de nombres relatifs de facteur négatif est égal à 4 est par conséquent est pair. Le signe du résultat est positif.
- (-2)*2*(-1)*2*(-1)*1*2*(-1) : Le nombre de nombres relatifs de facteur négatif est égal à 4 est par conséquent est pair. Le signe du résultat est positif.
Comment prendre des cours de maths 3eme ?
Division des nombres relatifs
Concernant les différents divisions entre des nombres de signe positif et négatif, on obtient les résultats suivants via la règle des signes :
- La division de deux nombres relatifs de même signe est positif
- La division de deux nombres relatifs de signes différents est négatif
Par exemple, la division de -2/1 donne un résultat négatif car les deux signes sont différents. A contrario, la division -2/-1 donne un résultat positif car les deux signes sont de même signe.
Addition et soustraction des nombres relatifs
Concernant les additions et soustractions de nombres relatifs, les règles suivantes s’appliquent :
- L’addition de deux nombres relatifs positifs donne un nombre relatif positif
- L’addition de deux nombres relatifs négatifs donne un résultat négatif
- L’addition d’un nombre relatif positif et d’un nombre relatif négatif varie selon la valeur de chacun des nombres
- La soustraction avec un nombre relatif correspond à l’addition d’un nombre relatif négatif. On peut noter par exemple 3 - 1 = 3 + (-1).

Exercice
Pour chacune des opérations suivantes, donner le signe du résultat et effectuer le calcul :
- (-3) + (-5)
- 3 - 5
- 4 + 6 - 3
- -3 + 3
- 4 + 5
- (-3) + (-2) + (-5) + 12
Corrigé
- (-3) + (-5) : Il s'agit de l'addition de deux nombres relatifs de signe négatifs. Le signe du résultat des deux nombres sera donc négatif. Pour calculer le résultat, il nous suffit simplement de faire l'addition des deux nombres relatifs puis ajouter le signe moins devant. On obtient donc (-3) + (-5) = -(3+5) = -8.
- 3 - 5 : Comme vu dans le quatrième point, la soustraction équivaut à l'addition avec un nombre relatif négatif. On peut donc écrire 3 - 5 = 3 + (-5). Le signe du résultat est moins évident car nous avons l'addition d'un nombre relatif de signe positif et un nombre relatif de signe négatif. Il nous faut donc effectuer le calcul : 3 - 5 = (-5) + 3 = -2.
- 4 + 6 - 3 : On peut effectuer l'addition en premier lieu pour n'avoir plus qu'une seule opération à gérer par la suite. 4 + 6 - 3 = 10 - 3. Ici la soustraction à effectuer est banale, on obtient donc 10 - 3 = 7.
- -3 + 3 : Pour faciliter le calculer, il vaut mieux transformer le nombre relatif négatif en une addition. On obtient alors -3 + 3 = 3 + (-3) = 3 - 3 = 0.
- 4 + 5 : Il s'agit la d'une simple addition, 4 + 5 = 9.
- (-3) + (-2) + (-5) + 12 : On effectue d'abord les opérations d'addition des nombres rationnels négatifs. (-3) + (-2) + (-5) = (-5) + (-5) = -10. Enfin, on transforme le reste de l'opération comme une simple soustraction : -10 + 12 = 12 - 10 = 2.
Les inégalités
Une inégalité est composée de deux membres séparés par des symboles ≤,≥,<,>. On note les différents signes comme suit :
- ≤ se prononce inférieur ou égal
- < se prononce strictement inférieur
- ≥ se prononce supérieur ou égal
- > se prononce strictement supérieur
La différence entre ces signes vient du fait que l'égalité est comprise ou non dans l'équation. Ainsi, on peut noter que 3 ≤ 5 ou 3 < 5 car 3 est inférieur à 5. En revanche, on ne peut que écrire 5 ≤ 5 car ce cas là prends en compte seulement l'égalité. Un nombre relatif négatif est toujours inférieur à un nombre relatif positif.
Exercice
Pour chacune des opérations suivantes, dire si ces inégalités sont vraies ou fausses :
- -3 ≤ 4
- 4 ≥ -2
- -4 ≤ -2
- 3 ≥ -4
- 4 ≤ -3
- - 8 ≥ -2
Corrigé
- -3 ≤ 4 Vrai : Un nombre relatif négatif est toujours inférieur à un nombre relatif positif
- 4 ≥ -2 Vrai : Inversement, un nombre relatif positif est toujours supérieur à un nombre relatif négatif
- -4 ≤ -2 Vrai : Pour les nombres relatifs négatifs, plus la valeur est élevée, plus ils sont petits
- 3 ≥ -4 Vrai : Un nombre relatif positif est toujours supérieur à un nombre relatif négatif
- 4 ≤ -3 Faux : Un nombre relatif positif est toujours supérieur à un nombre relatif négatif
- - 8 ≥ -2 Faux : Le nombre relatif négatif le plus grand est toujours le plus petit












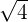

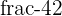












Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !