Chapitres

Introduction
Taille de l’univers (ordre de grandeur) : 10 000 000 000 000 000 000 000 000 m
Taille du noyau atomique (ordre de grandeur) : 0,000 000 000 000 001 m
Peu pratique, non ? Lorsque les nombres sont de l'ordre de l'infiniment grand ou de l'infiniment petit il devient long et difficile d'afficher le nombre de zéro correspondant. Même lorsque vous voulez afficher un très grand chiffre sur votre calculatrice, vous remarquerez que passé une certaine valeur, il n'est plus possible d'afficher ces chiffres.
Pour mieux visualiser les ordres de grandeur des nombres très grands et très petits, voici un tableau qui présente leur écriture décimale et leur équivalent en puissance de 10 :
| Exemple | Écriture décimale | Écriture en puissance de 10 |
|---|---|---|
| Taille de l’univers | 10 000 000 000 000 000 000 000 000 m | 1025 m |
| Taille d’un noyau atomique | 0,000 000 000 000 001 m | 10-15 m |
| 1 million | 1 000 000 | 106 |
| 0,001 | 0,001 | 10-3 |
Les puissances vont ainsi permettre deux choses :
- 1. La première qui semble évidente lorsque l'on voit les valeurs est de simplifier l'écriture des très grands et très petits nombres. Ils deviennent alors bien plus lisibles et peuvent être écrits sur n'importe quel support
- 2. La deuxième est de pouvoir comparer en un seul coup d’œil la différence d'ordre de grandeur entre les nombres. Entre 10 et 100, il est facile de voir que 100 est bien plus grand que 10 car il a un zéro de plus. Cependant, lorsque le nombre de zéros devient trop important, il devient bien plus difficile de pouvoir lire convenablement ce qui va faire la différence. La représentation sous forme de puissance de 10 permettra ainsi de pallier ce problème.
En cours de maths, le principe de base des puissances de 10 repose sur le concept défini ci-après :
Soit n un entier positif, on note
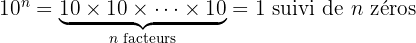
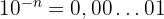
Soit n et p des entiers  et
et 
Nous expliciterons plus en détails après cette introduction comment maîtriser et manipuler les puissances de 10.

Définition et vocabulaire
Définition :
Soit n un nombre entier positif :  = 10 * 10 * 10 * ... * 10 (n fois) et
= 10 * 10 * 10 * ... * 10 (n fois) et  .
.
Soit n un nombre entier positif. On définit le nombre 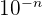 de la façon suivante :
de la façon suivante : 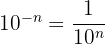
Exemples :


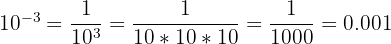
Cas pratique : Écrire la taille de l’univers sous la forme d’une puissance de 10 . La taille de l'univers est donné en introduction.
Cas particuliers :
Si n = 2, on dit que 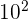 est le « carré » de 10, se lit « dix au carré » .
est le « carré » de 10, se lit « dix au carré » .
Si n = 3, on dit que 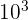 est le « cube » de 10, se lit « dix au cube ».
est le « cube » de 10, se lit « dix au cube ».
Au-delà, on dit simplement "dix puissance n" avec n étant la valeur de l'exposant.
Remarque : L’exposant est toujours prioritaire sur les autres opérations : 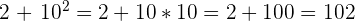
Règles de calcul sur les puissances de 10
1. Propriété n° 1 : produit de puissances.
Soient a et b deux entiers relatifs. Le produit de la puissance de a par b est égal à : 
Exemple :
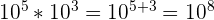
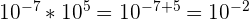
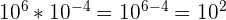
2.Propriété n° 2 : puissance de puissance.
Soient a et b deux entiers relatifs : 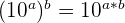
Exemple :
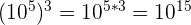


3.Propriété n° 3 : quotient de puissances.
Soient a et b deux entiers relatifs : 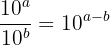
Exemple :
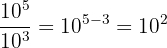
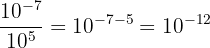
Vous cherchez un cours de maths seconde ?
Écriture scientifique

Propriété : Un nombre décimal admet plusieurs écritures sous la forme de produit d’un décimal par une puissance de 10
Exemple : 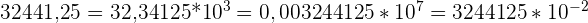
Définition : Écrire un nombre sous forme scientifique, c’est l’écrire sous la forme :  avec 1 < a < 10
avec 1 < a < 10
Exemples d’écritures scientifiques :
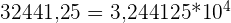 avec 1 < 3,244125 < 10
avec 1 < 3,244125 < 10
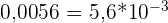 avec 1 < 5,6 < 10
avec 1 < 5,6 < 10
L'ensemble de la communauté scientifique doit souvent écrire de très grands ou de très petits nombres. Ils ont alors recours à une notation particulière appelée notation scientifique. Les nombres sont écrits, en notation scientifique, sous la forme générale : a × 10n avec 1 ≤ a < 10 (ou -10 < a ≤ -1) et n est un nombre entier relatif. Cette écriture permettra ainsi d'accorder l'ensemble de la communauté scientifique sur une même notation pour pouvoir plus facilement travailler ensemble.
Quelques exemples: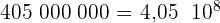


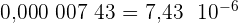
Exemples :
• 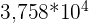 est une écriture scientifique
est une écriture scientifique
• 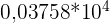 n'est pas une écriture scientifique car le chiffre devant la virgule est 0. Ce chiffre n'est donc pas compris entre 1 et 10.
n'est pas une écriture scientifique car le chiffre devant la virgule est 0. Ce chiffre n'est donc pas compris entre 1 et 10.
Cas pratique : Donner l'écriture scientifique de  :
:
Comme 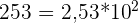 alors
alors 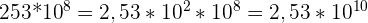
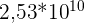 est l'écriture scientifique cherchée.
est l'écriture scientifique cherchée.
Intérêt: La notation scientifique des nombres relatifs permet, entre autres, de les comparer. Lorsque les deux nombres sont sous forme d’écritures scientifiques, on compare d’abord les exposants respectifs :
- S’ils sont différents, les nombres sont classés dans le même ordre que les exposants
- S’ils sont égaux, les nombres sont classés suivant le nombre devant la puissance de 10
Exemples : Comparer  et
et 
 est déjà sous forme d’écriture scientifique
est déjà sous forme d’écriture scientifique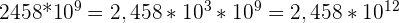
Dans l’exemple, les exposants sont égaux à 12 mais 2,458 < 3,48. Donc  . Si les exposants avaient été différents, il aurait simplement fallu comparer les valeurs des exposants.
. Si les exposants avaient été différents, il aurait simplement fallu comparer les valeurs des exposants.
Notation : On note l'ensemble des puissances de 10 comme dans le tableau comme suit :
| Puissance de 10 | Préfixe | Symbole |
|---|---|---|
| 10^24 | yotta | Y |
| 10^21 | zetta | Z |
| 10^18 | exa | E |
| 10^15 | péta | P |
| 10^12 | téra | T |
| 10^9 | giga | G |
| 10^6 | méga | M |
| 10^3 | kilo | K |
| 10^2 | hecto | H |
| 10^1 | déca | Da |
| 10^-1 | déci | D |
| 10^-2 | centi | C |
| 10^-3 | milli | M |
| 10^-6 | micro | µ |
| 10^-9 | nano | N |
| 10^-12 | pico | P |
| 10^-15 | femto | F |
| 10^-18 | atto | A |
| 10^-21 | zepto | Z |
| 10^-24 | yocto | Y |
Exercices
Maintenant, passons aux choses sérieuses ! Entraînez-vous sur ces exercices sur les puissances :
Il n’est pas rare en Sciences, d’avoir à effectuer des opérations sur des nombres dont l’écriture contient « beaucoup de zéros ».
Exemple : Calculer (1 000 000 )2
En mathématique on préfère écrire ce nombre ..............., ce qui se lit .....
Calcul : 1 000 000 × 1 000 000 = 1 000 000 000 000
Écriture en puissance de 10 : 1012, se lit "dix puissance 12"
Exprimer à l’aide d’une puissance de dix :
- 100 =
- 1 000 =
- un million =
- un milliard =
- 10 =
- 100 = 102
- 1 000 = 103
- 1 000 000 = 106
- 1 000 000 000 = 109
- 10 = 101
Compléter à l’aide d’une puissance de dix :
- 1 km = ? m
- 1 hg = ? g
- 1 m2 = ? mm2
- 1 km = ? cm
- 1 tonne = ? kg
- 1 l = ? cm3
- 1 dam = ? cm
- 1 m2 = ? cm2
- 1 m3 = ? l
- 1 km = 103 m
- 1 hg = 102 g
- 1 m2 = 106 mm2
- 1 km = 105 cm
- 1 tonne = 103 kg
- 1 l = 103 cm3
- 1 dam = 102 cm
- 1 m2 = 104 cm2
- 1 m3 = 103 l
Effectuer sans calculatrice :
- 345 × 103 =
- 0,345 × 102 =
- 0,0345 × 105 =
- 34,5 × 104 =
- 0,04 × 104 =
- 4 × 102 =
- 345 × 103 = 345 000
- 0,345 × 102 = 34,5
- 0,0345 × 105 = 3 450
- 34,5 × 104 = 345 000
- 0,04 × 104 = 400
- 4 × 102 = 400
La planète Saturne est à un milliard quatre cent vingt huit millions de kilomètres du soleil. Parmi ces écritures, lesquelles donnent cette distance ?
- 1 428 × 106
- 142,8 × 106
- 1,428 × 109
- 0,1428 × 1010
1 428 000 000 km = 1,428 × 109 km → réponse correcte : 1,428 × 109
En chimie, le nombre d’atomes contenus dans un gramme d’hydrogène est 602 000 000 000 000 000 000 000. Ce chiffre s’écrit 6,02 · 10 ..........
6,02 × 1023
En Sciences, on est aussi conduit à travailler avec des nombres dont l’écriture contient « beaucoup de zéros après la virgule ».
Exemple : Calculer (0,00001)2 : ?
En mathématique on préfère écrire ce nombre ............., et le lire ......................................................
(0,00001)2 = 1 × 10–10
Lecture : "une fois dix puissance moins dix"
Exprimer à l’aide d’une puissance de dix :
- 0,000000001 =
- 0,01 =
- un millionième =
- 0,0001 =
- 0,000000001 = 1 × 10–9
- 0,01 = 1 × 10–2
- un millionième = 1 × 10–6
- 0,0001 = 1 × 10–4
Compléter à l’aide d’une puissance de dix :
- 1 mg = ? g
- 1 cm = ? m
- 1 ml = ? hl
- 1 cm2 = ? m2
- 1 cm3 = ? m3
- 1 mm3 = ? l
- 1 mg = 10–3 g
- 1 cm = 10–2 m
- 1 ml = 10–5 hl
- 1 cm2 = 10–4 m2
- 1 cm3 = 10–6 m3
- 1 mm3 = 10–6 l
Donner l’écriture décimale des nombres suivants :
- 10–3 = ?
- 10–1 = ?
- 10–6 = ?
- 14,75 × 10–4 = ?
- 0,747 × 10–3 = ?
- 4 300 × 10–3 = ?
- 10–3 = 0,001
- 10–1 = 0,1
- 10–6 = 0,000001
- 14,75 × 10–4 = 0,001475
- 0,747 × 10–3 = 0,000747
- 4 300 × 10–3 = 4,3























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
heu salut je suis en 3ème et je n’ai pas compris le sours sur les puissances de 10 alors merci pour le cours que tu as donné ^^