Chapitres
? Le triangle ? Rien de plus simple ! On sait parfaitement l'étudier : ses angles, ses côtés, son centre de gravité, ses bissectrices, ses médiatrices... Mais cela est il si simple ? Regardons dans cet article la trigonométrie dans un triangle rectangle.
?? La trigonométrie à de nombreuses applications dans le domaine de la physique comme en astronomie mais aussi en navigation. Voici un résumé des fonctions trigonométriques à connaître et comment les utiliser en maths !
| Fonction Trigonométrique | Définition | Exemple |
|---|---|---|
| Sinus (sin) | Rapport du côté opposé sur l'hypoténuse dans un triangle. | Dans un triangle ABC, sin(A) = a/c. |
| Cosinus (cos) | Rapport du côté adjacent sur l'hypoténuse dans un triangle. | Dans un triangle ABC, cos(A) = b/c. |
| Tangente (tan) | Rapport du côté opposé sur le côté adjacent dans un triangle. | Dans un triangle ABC, tan(A) = a/b. |
| Sécante (sec) | Réciproque du cosinus : sec(A) = 1/cos(A). | sec(A) = 1/cos(A). |
| Cosécante (csc) | Réciproque du sinus : csc(A) = 1/sin(A). | csc(A) = 1/sin(A). |
| Cotangente (cot) | Réciproque de la tangente : cot(A) = 1/tan(A). | cot(A) = 1/tan(A). |

Définitions et applications ♾️

Les fonctions trigonométriques, telles que le sinus (sin), le cosinus (cos), la tangente (tan), la sécante (sec), la cosécante (csc) et la cotangente (cot), sont des outils fondamentaux en mathématiques et en sciences.
Ces fonctions, définies dans le contexte des triangles et des cercles, sont interconnectées par des relations réciproques et des identités, jouant un rôle essentiel dans la modélisation et l'analyse de phénomènes variés.
Sinus (sin)
Le sinus d'un angle A dans un triangle est défini comme le rapport du côté opposé a sur l'hypoténuse c.
Mathématiquement, cela est exprimé par la formule sin(A)=ca
Cette formule illustre la relation fondamentale entre les côtés d'un triangle et permet de mesurer l'angle en fonction de ces rapports.
? Le sinus est limité à des valeurs entre -1 et 1. Plus précisément, −1 ≤sin(A)≤1−1≤sin(A)≤1. Il atteint sa valeur maximale de 1 lorsque l'angle A est de 90 degrés (un angle droit), et sa valeur minimale de -1 lorsque l'angle est de 270 degrés. Les oscillations périodiques du sinus en font une fonction trigonométrique fondamentale.
- On définit le sinus d'un angle comme le rapport de la longueur du côté opposé à l'angle par la longueur de l'hypoténuse. Autrement dit, on note [sinus=\frac{oppose}{hypotenuse}]
- Cela donne
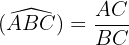
⚓️ Les applications du sinus sont diverses :
- En navigation, le sinus est utilisé dans la méthode d'altitude pour calculer la hauteur d'objets tels que les étoiles
- En ingénierie, il intervient dans l'analyse des forces dans des structures triangulées, où les composants verticaux des forces peuvent être déterminés en utilisant le sinus
Cosinus (cos)
Le cosinus d'un angle A dans un triangle est défini comme le rapport du côté adjacent b sur l'hypoténuse c.
Mathématiquement, cela est exprimé par la formule cos(A)=c/b
Cette formule représente la relation cruciale entre les côtés d'un triangle et offre une mesure de l'angle en fonction de ces proportions.
Le cosinus est borné entre -1 et 1, précisément −1≤cos(A)≤1−1≤cos(A)≤1. Il atteint son maximum de 1 lorsque l'angle A est de 0 degrés et son minimum de -1 lorsque l'angle est de 180 degrés. Le cosinus partage la périodicité du sinus, étant également une fonction trigonométrique fondamentale.
Dans un triangle rectangle, on définit le cosinus d'un angle comme le rapport de la longueur du côté adjacent à l'angle par la longueur de l'hypoténuse :
- On note [cos =\frac{adjacent}{hypotenuse}]
- Cela donne
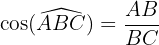
?♂️ Les applications du cosinus sont multiples :
- En trigonométrie, il est essentiel pour calculer les angles d'inclinaison en géométrie
- En ingénierie, il intervient dans l'analyse des forces et des tensions dans des structures
Elle permet de retenir les trois formules : sinus = opposé / hypoténuse, cosinus = adjacent / hypoténuse et tangente = opposé / adjacent
Tangente (tan)
La tangente d'un angle A dans un triangle est définie comme le rapport du côté opposé a sur le côté adjacent b.
Mathématiquement, cela est exprimé par la formule tan(A)=b/a
♾️ Cette formule incarne la relation trigonométrique fondamentale entre les côtés d'un triangle. La tangente n'a pas de limites spécifiques, mais elle devient infinie lorsque l'angle A approche de 90 degrés. Elle partage la périodicité des fonctions trigonométriques.
- La fonction tangente d'un angle comme le rapport de la longueur du côté opposé à l'angle par la longueur du côté adjacent à l'angle. On note [tan=\frac{oppose}{adjacent}]
- n obtient
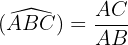
✨ La tangente est largement utilisée en trigonométrie pour résoudre des triangles. Elle intervient dans la physique pour calculer les angles d'inclinaison des surfaces. Son utilité s'étend également à d'autres domaines tels que l'ingénierie, la navigation et l'astronomie.
Sécante (sec)
La sécante d'un angle A dans un triangle est définie comme la fonction réciproque du cosinus, soit sec(A)=cos(A)1. Cette formule exprime la relation inverse entre la sécante et le cosinus dans le contexte trigonométrique.
La sécante partage les propriétés du cosinus, mais sa principale caractéristique réside dans le fait qu'elle représente l'inverse du cosinus. Elle n'est pas bornée.
?? En physique et en ingénierie, la sécante est utilisée pour analyser les forces et les tensions dans des structures triangulées. Son rôle réside dans la résolution de problèmes trigonométriques impliquant des triangles rectangles.
Cosécante (csc)
La cosécante d'un angle A dans un triangle est définie comme la fonction réciproque du sinus, soit csc(A)=sin(A)1. Cette formule exprime la relation inverse entre la cosécante et le sinus dans le contexte trigonométrique.
La cosécante partage les propriétés du sinus, mais sa caractéristique majeure réside dans le fait qu'elle représente l'inverse du sinus. Elle n'est pas bornée.
? La cosécante est fréquemment utilisée en physique, notamment dans l'étude des ondes et des phénomènes vibratoires. En ingénierie, elle intervient dans l'analyse des forces et des contraintes dans des structures triangulées.
Cotangente (cot)
La cotangente d'un angle A dans un triangle est définie comme la fonction réciproque de la tangente, soit cot(A)=tan(A)1. Cette formule exprime la relation inverse entre la cotangente et la tangente dans le contexte trigonométrique.
La cotangente partage les propriétés de la tangente, mais sa caractéristique principale réside dans le fait qu'elle représente l'inverse de la tangente. Elle n'est pas bornée.
? La cotangente trouve des applications pratiques dans divers domaines pour résoudre des problèmes trigonométriques variés :
- En trigonométrie, la cotangente est utilisée pour résoudre des triangles et des problèmes liés aux angles d'inclinaison
- En physique, elle intervient dans le calcul des angles de phase en optique
Interfonctionnalités trigonométriques ⛳️

Les six fonctions trigonométriques (sinus, cosinus, tangente, sécante, cosécante, cotangente) sont interconnectées par des relations réciproques et des identités fondamentales. Voici comment ces fonctions sont liées :
Relation fondamentale
- sin2(A)+cos2(A)=1
- C'est l'identité trigonométrique fondamentale qui lie le sinus et le cosinus. Elle découle directement du théorème de Pythagore dans un triangle rectangle
Relations réciproques

Ces relations démontrent les liens réciproques entre les fonctions. Par exemple, la tangente est le rapport du sinus sur le cosinus.
Identités additionnelles
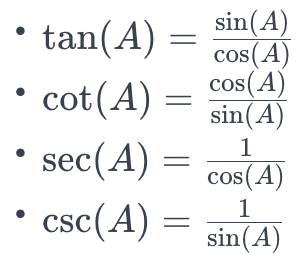
Ces identités montrent comment chaque fonction peut être exprimée en termes de sinus et cosinus.























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Bonsoir les membres de SUPERPROF, je vous félicite pour le cours, alors pouvous-nous m’aider à comprendre plus facilement le tableau trigonometrique?
Merci!
calculer df dans
triangle def rectangle en d avec de = 5cm et dfe = 65°
(il faut trouver df
Bonjour Ethan ! Avez-vous essayé de contacter l’un de nos professeurs pour recevoir une aide personnalisée ? Excellente journée ! :)
Besoin d’aide en mathématiques
Bonjour, avez-vous essayé de contacter l’un de nos professeurs de mathématiques pour recevoir une aide personnalisée ?
Je besoin d’un professeur pour l’encadrement en cours de cous de mathématiques, car je suis en classe de préparatoire polytechnique
Bonjour, il nous ferait plaisir de vous aider, n’hésitez pas à contacter nos professeurs sur la plateforme superprof :)