Chapitres
Introduction
Le développement, c'est quoi ? En mathématiques, comme lors d'une rédaction de français, développer signifie détailler, exposer, étendre un sujet, ou dans notre cas une expression littérale. Regardons les différents développements que l'on rencontre en mathématiques au collège.
Les parenthèses
Commençons par apprendre à développer les expressions littérales afin de les simplifier, notamment en supprimant des parenthèses.
Le but du développement et de détailler une expression dans le but de pouvoir la simplifier.
Par exemple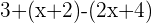 
Comment retire-t-on les parenthèses ?
Lorsque celle-ci est précédée par le signe "+", on peut retirer la parenthèse : elle est inutile.
Lorsqu'elle est précédée par le signe "-", on doit changer tous les signes présents dans la parenthèse pour la supprimer. Lorsque l'on retire la parenthèse, les signes "+" deviennent des "-" et les signes "-" deviennent des "+".
En effet, cela s'explique par le fait que la multiplication de deux nombres négatifs donne un nombre positif.
On obtient alors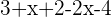 
On peut alors simplifier l'expression et obtenir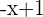 
Passons à la distributivité, c'est-à-dire développer un produit afin d'obtenir des sommes.
Commençons par la distributivité simple, c'est à dire un terme seul multiplié par une somme entre parenthèses, par exemple [3(2x+1)]
Pour supprimer la parenthèse, il faut distribué, multiplié le "3" par "2x" ainsi que par "1".
On obtient le calcul suivant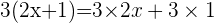 
On peut finalement simplifier et obtenir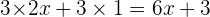 
De manière générale, on utilisera les formules suivantes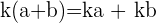 
et 
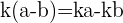
Cela revient à dire que la multiplication est distributive par rapport à l'addition et à la soustraction.
On dit que l'on a développé l'expression. Lorsqu'on le fait dans le sens contraire,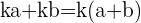 
on dit que l'on a factorisé, c'est à dire exprimé l'expression sous forme d'un produit. Ainsi, k(a+b) est la forme factorisée et ka+kb est la forme développée.
Passons maintenant à la double distributivité, c'est à dire à la multiplication de deux parenthèses contenant chacune une somme.
Par exemple,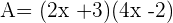 
La double distributivité se traduit par la formule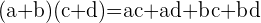 
Ainsi pour notre exemple on a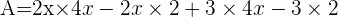 
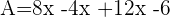
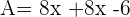
Finalement, la double distributivité signifie appliquer deux fois la distributivité simple.
Récapitulons ces différentes propriétés à travers des exemples :
| Que doit-on utiliser ? | Forme développée | Forme factorisée | |
|---|---|---|---|
| 3x-2-(3x+4) | supprimer la parenthèse en inversant les signes qu'elle contient | 3x-2-3x-4 =-6 | -6 |
| (x+4)+(3x) | On supprime les parenthèses : elles sont inutiles | x+4+3x=4x+4 | 4(x+1) |
| 3x(4+x-5x) | On utilise la distributivité | 12x +3x²-15x² =12x-12x² | 12x(1-x) |
| -(2x+5)(2-x) | On applique la double distributivité puis on change les signes de la parenthèse obtenue pour la supprimer | -(4x-2x²+10-5x) =-4x+2x²-10+5x =2x²+x-10 | (x-2)(2x+5) |
Les identités remarquables
Les identités remarquables sont des égalités importantes en mathématiques. Elles sont issues de la double distributivité.
Elles permettent de développer un produit particulier en somme et donc de supprimer les parenthèses. Il y en a trois à connaître :
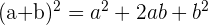
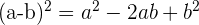
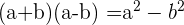
où a et b peuvent être des nombres comme des inconnues.
En réalité, ces identités remarquables sont simplement des doubles distributivités que l'on apprend pour être plus rapide lors de calculs. Regardons la démonstration de la première identité remarquable :
On sait que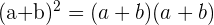 
En développant grâce à la double distributivité, on obtient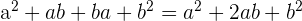 
Par exemple,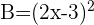 
On applique la deuxième identité remarquable :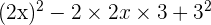 
Il ne reste qu'à simplifier :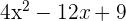 
On peut utiliser les identités remarquables dans l'autre sens pour factoriser une expression littérale.
Récapitulons en regardant différents exemples :
| Quelle identité remarquable a t on ? | Forme développée | |
|---|---|---|
| (x+3)(x-3) | La 3ème | x²-9 |
| (2x+5)² | La 1ère | 4x²+20x+25 |
| (3-x)² | La 2ème | 9-6x+x² |
| (2x+1)(2x-1) | La 3ème | 4x²-1 |
Dans les identités remarquables que nous apprenons, les parenthèses sont mises au carré. Il existe également d'autres formules lorsque les parenthèses sont élevées à une puissance plus importante, au cube par exemple. Une formule permet de généraliser les identités remarquables à n'importe quelle puissance : c'est le binôme de Newton.
Où trouver des cours de maths 3ème ?
Définition d'une puissance
On note x un entier relatif (positif ou négatif). Lorsqu'on le multiplie par lui même n fois (n un entier relatif), c'est à dire que l'on calcule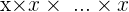 
où "x" apparaît n fois, on note le calcul 
On dira alors que est une puissance de x est que n est l'exposant.
Par convention, tout nombre non nul élevé à la puissance 0 vaut 1 :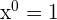 
Par exemple, 
signifie 
et vaut 16.
Les puissances sont donc un moyen d'écrire les multiplications répétées, de la même façon que la multiplication permet d'écrire les additions répétées.
Lorsqu'un nombre négatif est élevé à une puissance, le résultat est :
- positif si la puissance est paire
- négatif si la puissance est impaire
Par exemple,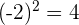 
et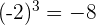 
Attention à ne pas oublier les parenthèses lorsque l'on met un nombre négatif en puissance !
Terminons par le cas des exposants négatifs. Prenons un exemple.
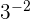peut aussi s'écrire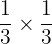 
De la même façon pour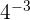 
on peut le développer en 
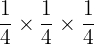Cela revient à écrire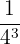 
Les opérations sur les puissances
Regardons les différentes opérations que l'on peut effectuer sur les puissances.
Attention, on ne peut pas simplifier les additions de puissances !
Par exemple, on ne peut pas simplifier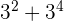 
Commençons par les multiplications de puissances. On a la formule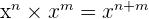 
Regardons comment l'utiliser.
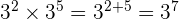En effet, si l'on détaille, on a 
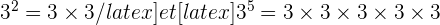Ainsi, on obtient bien 
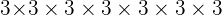soit bien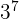 
Il en est bien-sûr de même pour les divisions. Pour x non nul, on a la formule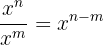 
Par exemple,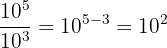 
On peut également effectuer des puissances de puissances.
En effet, on a la propriété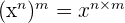 
Par exemple,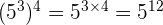 
On dénote quelques autres propriétés déjà vu au collège :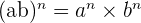 
et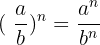 
Par exemple,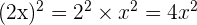 
Attention car sans la parenthèse, le calcul n'est pas le même ! 2x² est différent de (2x)²=4x²
Un autre exemple est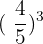 
qui est égal à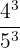 
Où trouver des cours de maths pour réviser avant une épreuve ?
L'écriture scientifique
Lorsqu'un nombre est très grand ou très petit, il est parfois long de l'écrire et difficile de le lire. Par exemple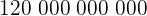 
ou encore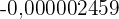 
On utilise alors les puissances de 10 pour écrire plus simplement ces nombres.
En effet, on a appris en 6ème que les multiplications par 10, 100, 1000, 0,1 et 0,01 consiste à ajouter, retirer des 0 ou à décaler la virgule.
On utilise alors l'écriture scientifique qui consiste à réécrire le nombre sous une autre forme. L'écriture scientifique d'un nombre positif est de la forme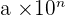 
où a est un nombre décimal compris entre 1 et 10 (soit avec exactement un chiffre non nul à gauche de la virgule) et n un entier relatif. Pour un nombre négatif, il en est de même avec le signe "-" qui précède a : 
Par exemple, 120 000 000 000 va devenir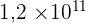 
et 0,000002459 s'écrit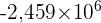 
Vous avez aimé cet article ? Notez-le !
Loading...
Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Bonne lecture et laisser un petit commentaire merci
Un petit commentaire.
Merci