Chapitres
- 01. Définition
- 02. Expérience aléatoire
- 03. Probabilité d'un évènement
- 04. Réunion et intersection de deux évènements
- 05. Exercices
- 06. Corrigés

Définition

Lorsqu'on lance un dé ou que l'on tire une carte au hasard, on réalise une expérience aléatoire dont chaque résultat est aussi appelé issue. Un événement est constitué d'une ou plusieurs issues. Exemple: On jette un dé et on repère le numéro obtenu. Il s'agit d'une expérience aléatoire. On obtient alors divers issues possibles, à savoir 1,2,3,4,5 ou 6. L'issue obtenir un nombre pair peut également un autre modèle d'issues. Ainsi chaque lancer peut être vu comme une probabilité d'obtenir une issue.
Expérience aléatoire
Définition
Une expérience (lancer un dé par exemple) est aléatoire lorsqu’elle a plusieurs résultats ou issues (1 ou 3 par exemple) qui ne peut pas être prévisible. On appelle l'ensemble des issues d’une expérience l’univers.
Exemples
On lance une pièce de monnaie et on regarde si c'est pile ou face. Il existe donc un univers constitué de deux issues (pile ou face). On lance un dé et on regarde le résultat. Il existe un un univers constitué de six issues (1, 2, 3, 4, 5 ou 6).
Cas pratique
Chaque élève lance 100 fois un dé à six faces et note les effectifs d’apparition de chaque face. On obtient le tableau suivant :
| Faces | 1 | 2 | 3 | 4 | 5 | 6 | Total |
|---|---|---|---|---|---|---|---|
| Effectifs | 20 | 14 | 10 | 22 | 16 | 18 | 100 |
| Faces | 1 | 2 | 3 | 4 | 5 | 6 | Total |
|---|---|---|---|---|---|---|---|
| Effectifs | 434 | 456 | 443 | 459 | 435 | 473 | 2700 |
| Fréquences | 16.1% | 16.9% | 16.4% | 17% | 16.1% | 17.5% | 100 |
Probabilité d'un évènement
Arbre de probabilité
Lorsqu’on fait tourner la roue, quatre issues sont possibles. On le schématise via un arbre de probabilité
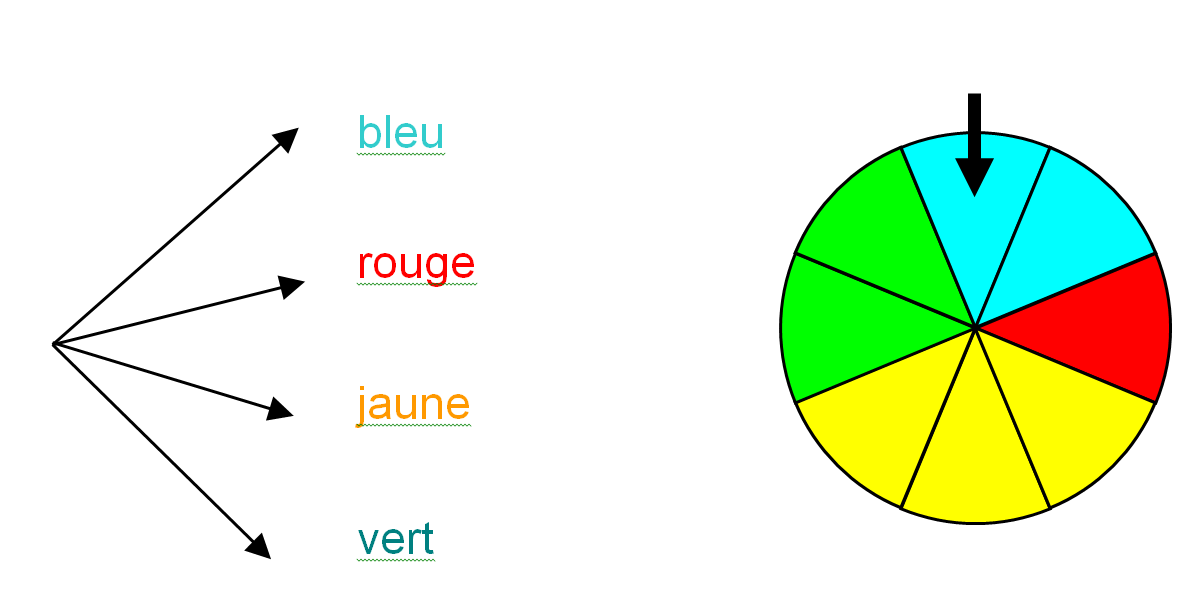
L'arbre de probabilité permet de visualiser les issues d’une expérience aléatoire.
Probabilités
2 secteurs sur 8 sont de couleur bleue. Lors d’une expérience aléatoire, il y a donc 2 chances sur 8 d’obtenir un secteur de couleur bleue. On dit que la probabilité d’obtenir un secteur bleu est égale à 2/8, soit 1/4 . On peut ensuite inscrire sur l'arbre des probabilités la valeur 2/8 ou 1/4. On affichera par conséquent sur la flèche menant à bleu la valeur 1/4, sur la flèche menant à rouge la valeur 1/8, sur la flèche menant à jaune la valeur 3/8 et sur la flèche menant à vert la valeur 1/4.
Évènements
Définition
On appelle l'évènement une issue possible d'une expérience aléatoire. Cette dernière permettra ainsi de définir une probabilité.
Pourquoi ne pas demander de l'aide en cours de maths en ligne ?
Comment utiliser le dénombrement pour calculer une probabilité ? On considère l’expérience aléatoire suivante : On tire une carte dans un jeu de 52 cartes. Soit E l’évènement : "On tire un as". Quelle est la probabilité que l’évènement E se réalise ? Il a 52 issues possibles car il existe 52 cartes différentes. Il est donc possible de tirer de manière équiprobable n'importe laquelle de ces 52 cartes. L’événement E possède 4 issues possibles : As de cœur, as de carreau, as de trèfle et as de pique. La probabilité que l’événement E se réalise est donc égale à : P(E) = 4/52 = 1/13 Comment calculer une probabilité en utilisant un arbre de probabilités ? On considère l’expérience aléatoire suivante : On lance un dé à six faces et on regarde le nombre de points inscrits sur la face du dessus. Soit E l’évènement : "La face du dessus est un 1 ou un 6". Quelle est la probabilité que l’évènement E se réalise ? On construit l’arbre des possibles de l’expérience aléatoire : Chaque issue à la même probabilité : il y a une chance sur six de sortir un 1, un 2, … ou un 6. On dit qu’il y a équiprobabilité. Ainsi P(E) = 1/3, ce qui se traduit par : La probabilité que l’évènement E se réalise est de 1/3. Il y a donc une chance sur trois d’obtenir un 1 ou un 6 en lançant un dé. On détermine différentes propriétés :
- La probabilité P(E) d’un événement E est telle : 0 ≤ P(E) ≤ 1.
- La somme des probabilités des événements élémentaires est égale à 1.
- La probabilité d’un événement est la somme des probabilités des événements élémentaires qui le constituent.
Comment progresser en cours de math 3eme ?
Évènements contraires
Exemple
On considère l’expérience aléatoire suivante : On lance un dé à six faces et on regarde le nombre de points inscrits sur la face du dessus. Soit E l’évènement : "La face du dessus est un 1 ou un 6". Alors l’évènement contraire de E est : « La face du dessus est un 2, un 3, un 4 ou un 5 ». Cet évènement est noté 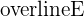 Propriété : La probabilité de l’événement contraire d’un événement E est : P(
Propriété : La probabilité de l’événement contraire d’un événement E est : P(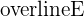 ) = 1 – P(E). La probabilité que l’évènement E se réalise est de . Il y a donc trois chances sur quatre d’obtenir au moins une fois la PILE lorsqu’on lance deux fois de suite une pièce de monnaie.
) = 1 – P(E). La probabilité que l’évènement E se réalise est de . Il y a donc trois chances sur quatre d’obtenir au moins une fois la PILE lorsqu’on lance deux fois de suite une pièce de monnaie.
Besoin d'un cours de maths ?
Réunion et intersection de deux évènements
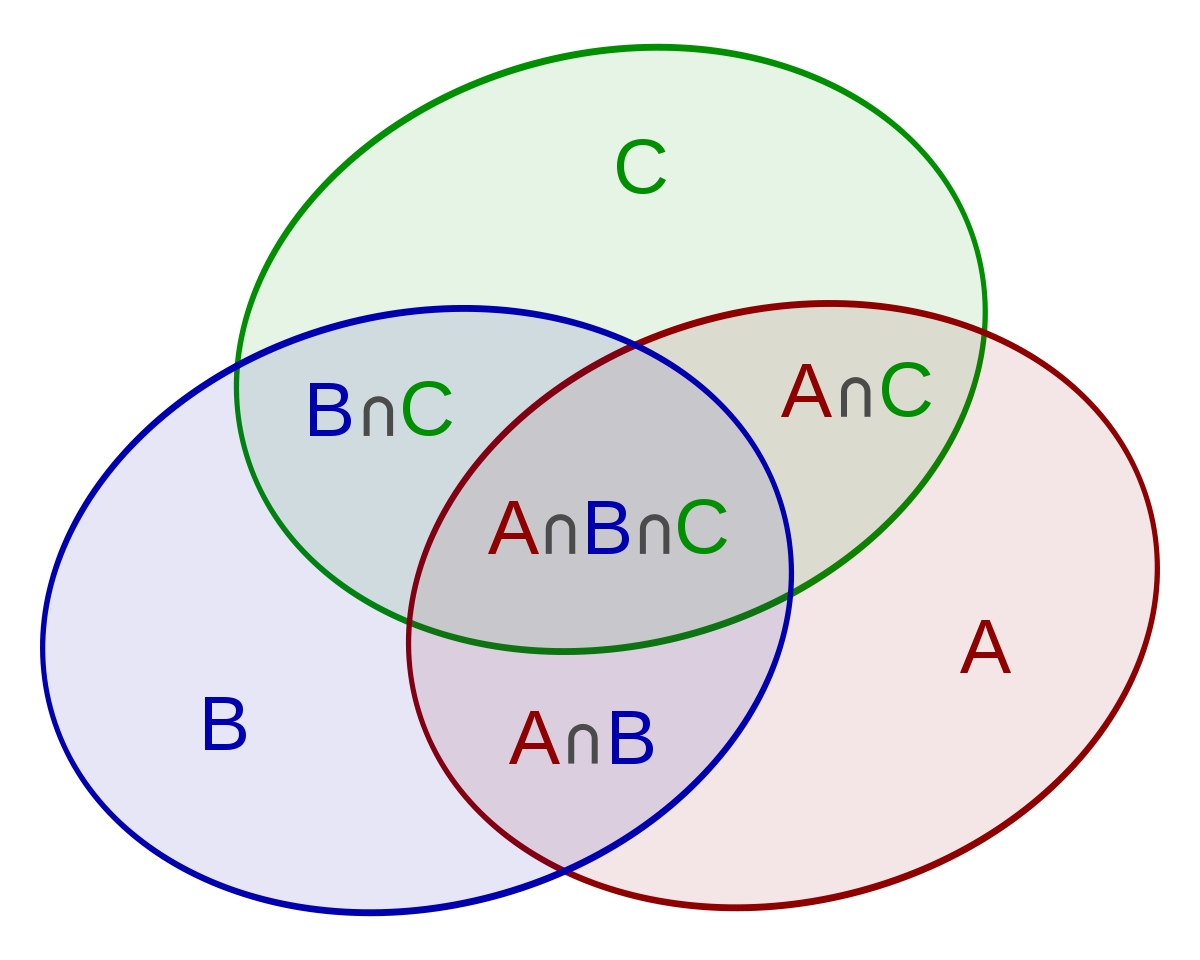
Définitions
- L'événement "A et B", noté A
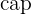 B, est un évènement réalisé lorsque les évènements A et B se réalisent en même temps.
B, est un évènement réalisé lorsque les évènements A et B se réalisent en même temps. - L'événement "A ou B", noté A
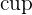 B, est réalisé lorsque un des deux évènements ou les deux évènements sont réalisés.
B, est réalisé lorsque un des deux évènements ou les deux évènements sont réalisés.
Exemple
On considère l’expérience aléatoire suivante : On tire une carte dans un jeu de 52 cartes à jouer. On considère les événements suivants :
- A : « On tire un valet »
- B : « On tire un cœur ou un carreau »
L’intersection des évènements A et B est l’évènement :"On tire le valet de cœur ou le valet de carreau". On note cet évènement A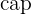 B et on lit "A inter B". La réunion des évènements A et B est l’évènement : "On tire un valet ou un tire un coeur ou un carreau". La réunion de ces évènements est donc on peut tirer n'importe quel coeur, n'importe quel carreau ou n'importe quel valet. On note cet évènement A
B et on lit "A inter B". La réunion des évènements A et B est l’évènement : "On tire un valet ou un tire un coeur ou un carreau". La réunion de ces évènements est donc on peut tirer n'importe quel coeur, n'importe quel carreau ou n'importe quel valet. On note cet évènement A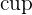 B et on lit « A union B ». Sur un jeu de 32 cartes, on obtient alors :
B et on lit « A union B ». Sur un jeu de 32 cartes, on obtient alors : 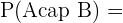 P(valet de coeur ou valet de carreau) = 2/52 = 1/26.
P(valet de coeur ou valet de carreau) = 2/52 = 1/26.  P(n'importe quel coeur ou n'importe quel carreau ou n'importe quel valet) = (13 + 13 + 2) = 28/52 = 7/13.
P(n'importe quel coeur ou n'importe quel carreau ou n'importe quel valet) = (13 + 13 + 2) = 28/52 = 7/13.
Probabilité d'une réunion
Théorème : Si A et B sont deux événements d'une expérience aléatoire, alors :  . Méthode : Calcul de probabilité en utilisant le théorème de probabilité d’une réunion On considère l’expérience aléatoire suivante : On lance un dé à six faces non pipé et on regarde le score obtenu pour le lancer du dés. On considère les événements suivants :
. Méthode : Calcul de probabilité en utilisant le théorème de probabilité d’une réunion On considère l’expérience aléatoire suivante : On lance un dé à six faces non pipé et on regarde le score obtenu pour le lancer du dés. On considère les événements suivants :
- A : « Le dés donne un résultat impair »
- B : « Le dés donne un multiple de 3 »
On souhaite calculer la probabilité de l’évènement 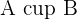 . P(A) = 1/2 et P(B) = 2/6 = 1/3.
. P(A) = 1/2 et P(B) = 2/6 = 1/3.  est l'événement élémentaire : « On obtient un 3 », donc
est l'événement élémentaire : « On obtient un 3 », donc  . L'événement
. L'événement  a donc pour probabilité :
a donc pour probabilité :  = 1/2 + 1/3 - 1/6 = 3/6 + 2/6 -1/6 = 4/6 = 2/3
= 1/2 + 1/3 - 1/6 = 3/6 + 2/6 -1/6 = 4/6 = 2/3
Vous cherchez des cours de maths seconde ?
Évènements incompatibles
On dit que deux événements A et B sont incompatibles si 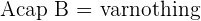 . Si deux événements A et B sont incompatibles alors
. Si deux événements A et B sont incompatibles alors  Exemple : On considère l’expérience aléatoire suivante : On tire une carte dans un jeu de 32 cartes à jouer. On considère les événements suivants :
Exemple : On considère l’expérience aléatoire suivante : On tire une carte dans un jeu de 32 cartes à jouer. On considère les événements suivants :
- A : « On tire un valet »
- B : « On tire un roi »
Les deux évènements A et B sont incompatibles, en effet 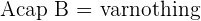 On en déduit que la probabilité de l’évènement « Tirer un valet ou un roi » est égale à :
On en déduit que la probabilité de l’évènement « Tirer un valet ou un roi » est égale à : 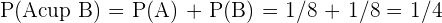
Exercices
Exercice 1 Pour chacun des cas suivants, indiquer à quoi correspond l'évènement considéré ainsi que sa probabilité associée
- Il est toujours en retard.
- Il y a une chance sur deux que le bus ne soit pas à l'heure
- Le beau temps est annoncé pour le week-end avec un indice de confiance de 3 sur 5.
- Il n’a aucune chance de battre ce record.
- Huit fois sur dix il oublie quelque chose.
Exercice 2 On a mélangé dans un sac 70 bonbons à la menthe et 45 chocolats au lait. Quelle est la probabilité de l’évènement N « tirer un bonbons à la menthe » ? Exercice 3 Kevin présente à ses amis un sac dans lequel se trouvent 50 bonbons dont 30 à la fraise, 15 à la menthe et 5 au citron. Mickael n’aime pas les bonbons à la menthe. Quelle est la probabilité qu’il soit satisfait s’il tire un bonbon sans regarder ? Exercice 4 On lance un dé pipé dont les faces ont été remplacées. Sur ces dernières, on lit désormais les numéros de faces différents à savoir les chiffres 1 ; 2 ; 2 ; 3 ; 3 ; 3.
- Construire un arbre des possibilités et déterminer la probabilité de sortir 1.
- Quelle est la probabilité de sortir un nombre impair ?
Exercice 5 On prends un jeu carte traditionnel de 52 cartes.

- Quelle est la probabilité de tirer un as ?
- Quelle est la probabilité de tirer un trèfle ?
- Quelle est la probabilité de tirer l’as de trèfle ?
Exercice 6 On lance 500 fois un dé pipé (les poids sont différents pour changer les fréquences). Le nombre d’apparitions de chaque face est noté : N° de la face | 1 | 2 | 3 | 4 | 5 | 6 Nombre d'apparitions | 75 | 80 | 90 | 85 | 78 | 92
- Quelle est la probabilité d’obtenir 4 ?
- Quelle est la probabilité d’obtenir un nombre pair ?
- Quelle est la probabilité d’obtenir un nombre impair ?
Exercice 7 On a placé 5 boules rouges, 3 boules bleues et 4 boules noires dans une urne.
- Construire un arbre des possibilités.
- Quelle est la probabilité de tirer une boule rouge ou une boule noire ?
- Quelle est la probabilité de ne pas tirer une boule rouge ?
Exercice 8 On lance deux fois une même pièce équilibrée.
- Construire un arbre des possibilités.
- Quelle est la probabilité d’obtenir deux fois « pile » ?
- Quelle est la probabilité d’obtenir deux tirages différents ?
Corrigés
Exercice 1 Dans chacun des cas suivants, indiquer l’évènement considéré, puis sa probabilité.
- Kevin est toujours en retard : Evenement : La probabilité d'être en retard.P(retard) = 1
- Il y a une chance sur deux que le bus ne soit pas à l'heure. Evènement : La probabilité que le bus soit à l'heure.P(bus à l'heure) = 1/2
- Le beau temps est annoncé pour le week-end avec un indice de confiance de 3 sur 5. Evènement : La probabilité qu'il fasse beau ce weekend. P(beau temps) = 3/5
- Il n’a aucune chance de battre ce record. Evènement : La probabilité de battre le record. P(battre le record) = 0
- Huit fois sur dix il oublie quelque chose. Evènement : La probabilité d'oublier quelque chose P(oubli) = 8/10
Exercice 2 Le nombre de confiseries dans le sac est égale à la somme des bonbons à la menthe et des chocolats au lait à savoir 70 + 45 = 115. La probabilité de tirer un bonbon à la menthe est donc de P(tirer bonbon à la menthe) = 70/115. Exercice 3 La probabilité que Patrice tire un bonbon à la menthe est de P(tirer bonbon menthe) = 15/50 = 0.3. Par conséquent, la probabilité de ne pas tirer un bonbon à la menthe est de 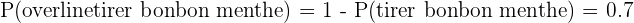 . Exercice 4 1. Une fois l'arbre construit, on voit que la probabilité de sortir 1 est de 1/6. 2. La probabilité de sortir un nombre impair est de 3/6 = 1/2. Exercice 5 On utilise un jeu de 52 cartes.
. Exercice 4 1. Une fois l'arbre construit, on voit que la probabilité de sortir 1 est de 1/6. 2. La probabilité de sortir un nombre impair est de 3/6 = 1/2. Exercice 5 On utilise un jeu de 52 cartes.
- Quelle est la probabilité de tirer un as ?
- Quelle est la probabilité de tirer un trèfle ?
- Quelle est la probabilité de tirer l’as de trèfle ?
1. Il existe 4 as dans un paquet de carte. La probabilité est donc de P(tirer un as) = 4/52 = 1/13. 2. Il y a 13 trèfles dans un paquet de carte. La probabilité est donc de P(tirer un trèfle) = 13/52 = 1/4. 3. Il y a un seul as de trèfle dans un paquet de carte. La probabilité est donc de P(tirer l'as de trèfle) = 1/52. Exercice 6 1. La probabilité d'obtenir 4 est de P(obtenir 4) = 85/500 = 0.17. 2. La probabilité d'obtenir un nombre pair est de P(obtenir un nombre pair) = (80 + 85 + 92) / 500 = 257/ 500 = 0.514. 3. La probabilité d'obtenir un nombre impair est de P(obtenir un nombre impair) = (75 + 90 + 78) / 500 = 243/ 500 = 0.486. Exercice 7 2. Selon l'arbre, la probabilité de tirer une boule rouge ou noir est de 5/12+ 4/12 = 9/12 = 3/4 = 0.75. 3. On calcule la probabilité de tirer une boule rouge : P(boule rouge) = 5/12. On calcule désormais la probabilité opposé : 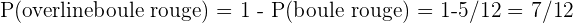 Exercice 8 2. La probabilité d'obtenir deux fois pile est égale à 1/2*1/2 = 1/4. 3. La probabilité d'obtenir deux tirages différents est égale à la probabilité d'obtenir pile puis face plus la probabilité d'obtenir face puis pile. On obtient donc : P(deux tirages différents) = 1/2*1/2 + 1/2*1/2 = 1/4 + 1/4 = 1/2
Exercice 8 2. La probabilité d'obtenir deux fois pile est égale à 1/2*1/2 = 1/4. 3. La probabilité d'obtenir deux tirages différents est égale à la probabilité d'obtenir pile puis face plus la probabilité d'obtenir face puis pile. On obtient donc : P(deux tirages différents) = 1/2*1/2 + 1/2*1/2 = 1/4 + 1/4 = 1/2
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Comment calculer la probabilité des points obtenus lorsqu’on lance deux dés cubiques à travers le tableau x/x ?
Puis-je avoirs un aide pour une exercices
Parfait merci
Puis je avoir un aide sur un’exercice
Bonjour, il nous ferait plaisir de vous aider, n’hésitez pas à contacter nos professeurs sur la plateforme de Superprof :)
Bonjour, si on dit que le dé est non pipé, et que il y’a n faces numérotées 2.Qu’est ce que ça veut dire