Chapitres

Introduction
Le plus grand commun diviseur, aussi connu sous le nom de PGCD, est nécessaire pour de nombreuses applications comme la simplification de fractions ou encore déterminer si deux nombres sont premiers entre eux. Étudions ses propriétés et ses différentes applications.
Rappel sur le PGCD

Soient a et b des entiers positifs.
On a vu en classe de 3ème que le PGCD de deux nombres a et b est le plus grand nombre qui divise à la fois a et b. Par exemple, le PGCD de 15 et 10 est 5. Pour déterminer le PGCD de deux nombres, on peut faire une liste des diviseurs de a puis de b et déterminer le plus grand diviseur commun.
Lorsque les nombres sont grands, on peut utiliser la factorisation en nombre premier pour déterminer le PGCD. Par exemple,  et
et 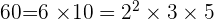 On a alors
On a alors 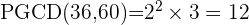
Le calcul du PGCD sert notamment pour rendre une fraction irréductible. Pour cela, il faut calculer le PGCD du numérateur et du dénominateur puis diviser l'ensemble de la fraction par le PGCD obtenu.
Par exemple, pour simplifier la fraction 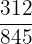 on calcule le PGCD de 312 et 845 puis on divise le numérateur et le dénominateur de la fraction par ce PGCD. On a
on calcule le PGCD de 312 et 845 puis on divise le numérateur et le dénominateur de la fraction par ce PGCD. On a 
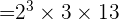 et
et 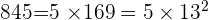 Donc le PGCD de 312 et 845 est 13. Ainsi on divise le numérateur et le dénominateur par 13, ce qui donne
Donc le PGCD de 312 et 845 est 13. Ainsi on divise le numérateur et le dénominateur par 13, ce qui donne 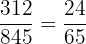 .
.
Définitions et propriétés du PGCD

Étudions maintenant de façon plus précise ce que représente le PGCD.
On note D(a) l'ensemble des diviseurs de a. Les éléments de D(a) sont tous inférieurs ou égaux à a. Lorsque a>1, D(a) contient au moins 1 et a. Le plus grand élément de D(a) est a et son plus petit est 1.
On note D(a,b) les diviseurs communs à a et à b. D(a,b) est l'intersection de D(a) et D(b). De plus, D(a,b)=D(b,a).
D(a,b) n'est pas vide puisqu'il contient 1. Tous ses éléments sont inférieurs ou égaux à a et inférieurs ou égaux à b. Donc D(a,b) contient un plus grand élément qui est appelé le PGCD.
Par exemple, on veut déterminer PGCD(6,15). D(6)={1,2,3,6} et D(15)={1,3,5,15}. Donc D(6,15)={1,3}. Ainsi, PGCD(6,15)=3.
Lorsque le PGCD vaut 1, on dit que a et b sont premiers entre eux.
Si b divise a, b différent de 0, alors tout diviseur de b divise aussi a d'où D(b) est inclus dans D(a). Ainsi, D(a,b)=D(b) et PGCD(a,b)=b.
Tout diviseur de deux entiers a et b est un diviseur de leur PGCD et réciproquement.
En cours de maths, un première méthode envisageable pour déterminer le PGCD est par soustractions successives. En effet, on a D(a,b)=D(b,a-b) où a>b. Montrons le. Montrons d'abord que si d appartient à D(a,b) alors d appartient à D(b,a-b). Si d appartient à D(a,b) alors d divise a et d divise b alors d divise b et d divise a-b. Donc d appartient à D(b,a-b). Montrons maintenant que si d appartient à D(b,a-b) alors d appartient à D(a,b). Si d appartient à D(b,a-b) alors d divise b et d divise a-b d'où d divise (a-b+b)=a. Donc d divise b et d divise a. Donc d appartient à D(a,b).
Cherchons le PGCD de 168 et 264. D(264,168)=D(168,264-168)=D(168,96)=D(96,168-96)=D(96,72)=D(72,96-72)=D(72,24)=D(24,72-24)=D(24,48)=D(24,48-24)=D(24,24)=D(24). Donc PGCD(264,168)=24.
L'algorithme d'Euclide

L'algorithme d'Euclide est une autre méthode pour calculer le PGCD de deux nombres : par divisions successives. Cette méthode consiste à exprimer d'abord le plus grand nombre en fonction du plus petit et d'un reste. Puis on exprime le plus petit en fonction du précédent reste et d'un nouveau reste. On continue ce procédé jusqu'à ce que l'on arrive à un reste nul. Le dernier reste non nul est alors le PGCD des deux nombres de départ.
Cette méthode est basée sur le fait que D(a,b)=D(b,r) où a=bq+r est la division euclidienne de a par b. Montrons le. Si d appartient à D(a,b) alors d divise a et d divise b alors d divise a et d divise b et d divise bq. Donc d divise b et d divise a-bq d'où d appartient à D(b,r). Donc D(a,b) est inclus dans D(b,r). Réciproquement, si d appartient à D(b,r) alors d divise b et d divise r. Donc d divise b et d divise a-bq d'où d divise b et d divise bq et d divise a+bq-bq=a. Ainsi d divise b et d divise a d'où d appartient à D(a,b). Donc D(b,r) est inclus dans D(a,b). En conclusion, D(a,b)=D(b,r).
Si r=0, alors b divise a et D(a,b)=D(b).
Prenons un exemple, calculons le PGCD de 144 et 840.
 D(840,144)=D(144,120)
D(840,144)=D(144,120)
 D(144,120)=D(120,24)
D(144,120)=D(120,24)
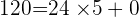 D(120,24)=D(24,0)=D(24).
D(120,24)=D(24,0)=D(24).
Donc PGCD(840,144)=24 puisque 24 est le dernier reste non nul.
Prenons un deuxième exemple en calculons le PGCD de 421 et 189.
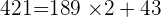
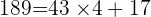

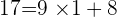

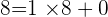
Le dernier reste non nul est 1 donc PGCD(421,189)=1. Donc 421 et 189 sont premiers entre eux.
Vous pourrez voir ça en cours de maths en ligne.
Exercices sur le PGCD

Exercice 1
Déterminer, à l'aide de la factorisation en nombres premiers, le PGCD de 56 et 24, le PGCD de 47 et 95, le PGCD de 126 et 42 et le PGCD de 452 et 289.
Exprimons les résultats dans le tableau ci-dessous :
| factorisation du premier nombre | factorisation du deuxième nombre | PGCD | |
|---|---|---|---|
| PGCD(56,24) | 56=2³x7 | 24=2³x3 | 2³=8 |
| PGCD(47,95) | 47 est un nombre premier | 95=5x19 | 1 |
| PGCD(126,42) | 126=2x7x3² | 42=2x3x7 | 2x7x3=42 |
| PGCD(452,289) | 452=2²x113 | 289=17² | 1 |
Exercice 2
Déterminer, à l'aide de l'algorithme d'Euclide, le PGCD de 145 et 127, le PGCD de 39 et 24, le PGCD de 265 et 487 et le PGCD de 327 et 642.
Donnons les résultats dans un tableau :
| Etape 1 | Etape 2 | Etape 3 | Etape 4 | Etape 5 | PGCD=dernier reste non nul | |
|---|---|---|---|---|---|---|
| PGCD(145,127) | 145=127x1+18 | 127=18x7+1 | 18=1x18+0 | 1 | ||
| PGCD(39,24) | 39=24x1+15 | 24=15x1+9 | 15=9x1+6 | 9=6x1+3 | 6=3x2+0 | 3 |
| PGCD(265,487) | 487=265x1+222 | 265=222x1+43 | 222=43x5+7 | 43=7x6+1 | 7=1x7+0 | 1 |
| PGCD(327,642) | 642=327x1+315 | 327=315+12 | 315=12x26+3 | 12=3x4+0 | 3 |
Exercice 3

Le calcul du PGCD peut servir pour résoudre certains problèmes. Par exemple, prenons le problème suivant :
Un commerçant reçoit 90 lampes de poches avec 135 ampoules et qu'il veut vendre des lots identiques sans qu'il ne lui reste d'ampoule ni de lampe. On peut se demander combien il devra mettre d'ampoules et de lampes dans chaque lot afin d'obtenir le plus de lot possible.
Le nombre de lots doit être un diviseur de 90 et également un diviseur de 135. On ne peut diviser le nombre d'ampoule ou de lampes que par un nombre entier et il ne doit rester ni lampe ni ampoule au commerçant. Pour obtenir le maximum de lots, il doit diviser 90 et 135 par le plus grand nombre possible. Il doit donc chercher le PGCD de 90 et de 135. On peut appliquer l'algorithme d'Euclide :
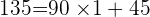

Donc PGCD(135,90)=45 et le commerçant peut faire un maximum de 45 lots contenants chacun 2 lampes (90 divisé par 45) et 3 ampoules (135 divisé par 45).























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
LES LAMPES : 90=42×2+0 ??? C’est pas plutôt 90=45×2+0
21/49son
Bonjour, effectivement une petite erreur s’est glissée dans le calcul, nous venons tout juste de corriger cette dernière et cela grâce à vous! Un grand merci pour votre attention :)