Chapitres
- 01. Définition
- 02. Les dérivées usuelles
- 03. Opérations et dérivées
- 04. Exercices corrigés

Définition
- Soit Df l’ensemble de définition d’une fonction f.
- Soit f(x) une fonction définie sur R de la variable x.
- On considère que la fonction f est dérivable en un point a si
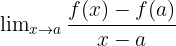 tend vers a.
tend vers a. - La fonction f est dérivable lorsque cette limite s’applique en tout point de la fonction.
- On note la dérivée de la fonction f(x) en f’(x).

Les dérivées usuelles
Dans ce tableau vous trouverez les dérivées usuelles pour les fonctions les plus communes.
| Fonctions | Ensemble de définition | Ensemble de dérivabilité | Dérivée | Remarque |
|---|---|---|---|---|
| λ | R | R | 0 | λ est une constante dans R |
| λx | R | R | λ | λ est une constante dans R |
| 1/x | R* | R* | -1/x2 | |
| √(x) | R+ | R+ | 1/(2√(x)) | |
| xn | R | R | nxn-1 | n est un entier naturel |
| x-n | R | R | -nx-n-1 | n est un entier naturel |
| ln (x) | R+ | R+ | 1/x | |
| ex | R | R | ex | |
| sin(x) | R | R | cos(x) | |
| cos(x) | R | R | -sin(x) | |
| tan(x) | R\((π/2+πZ) | R\((π/2+πZ) | 1+tan2(x) |
- La dérivée d'une constante est égale à 0 car son coefficient directeur est nul (le tracé d'une fonction constante est une ligne horizontale)
- Si l'on n'arrive pas à se souvenir de la dérivée de
 , on peut raisonner de la manière suivante :
, on peut raisonner de la manière suivante : 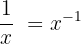 . A partir de cette constatation, on peut appliquer la formule de la dérivée de
. A partir de cette constatation, on peut appliquer la formule de la dérivée de  avec n=1
avec n=1 - La dérivée de la fonction exponentielle est la fonction exponentielle. C'est justement une propriété de cette fonction

La fonction exponentielle et sa dérivée sont identiques
- Le calcul de la dérivée permet d'obtenir le coefficient directeur de la fonction. Si la dérivée est négative sur un interval, la fonction sera décroissante et inversement, si la dérivée est positive sur un interval la fonction sera croissante

- Concernant la fonction tan(x), l'ensemble de définition est privé de
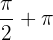 Z car cela correspond au modulo de valeurs pour lesquelles la fonction cos(x) est égale à 0. Pour rappel, on sait que tan(x) =
Z car cela correspond au modulo de valeurs pour lesquelles la fonction cos(x) est égale à 0. Pour rappel, on sait que tan(x) = 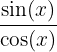
Pourquoi ne pas demander de l'aide en cours de maths en ligne ?
Opérations et dérivées
Le premier tableau a permis de découvrir les fonctions usuelles. Cependant, on ne travaille que très rarement sur les fonctions usuelles. Il s'agit la plupart du temps de composition de fonctions usuelles. Dans ces cas la, on applique le calcul des dérivées comme suit :
| Fonction | Dérivée |
|---|---|
| λ *u | λ *u' |
| u+v | u'+v' |
| 1/u | -u'/u2 |
| u*v | u'v+uv' |
| u/v | (u'v-uv')/v2 |
Exercices corrigés
Exercice
Pour chacune des fonctions suivantes, donner l'ensemble de définition de la fonction, l'ensemble de dérivabilité et la dérivée. Les exercices ont été placés par ordre de difficulté croissant.
Corrigé
f(x) est une fonction définie et dérivable sur R. La fonction est sous la forme λ * u avec λ = 3 et u = x. D'après le tableau des dérivées usuelles, on obtient u' = 1. D'où 
f(x) est une fonction définie et dérivable sur R. La fonction est sous la forme λ avec λ = 10. Or la dérivée d'une constante est égale à 0. D'où 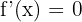
ln(x) étant définie et dérivable sur R+, f(x) est définie et dérivable sur R+. La fonction est sous la forme λ*u avec λ = 3 et u = ln(x). D'après le tableau des dérivées usuelles on sait que u'= (ln(x))' = 1/x. D'après le tableau des opérations et dérivées, on sait que la dérivée de λ*u est λ*u'. D'où 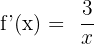
f(x) étant un polynôme de degré 3, elle est définie et dérivable sur R. La fonction polynomiale est une somme d'éléments avec des coefficients différents sous la forme 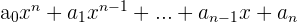 Pour calculer la dérivée d'un polynôme on calcule donc séparément la dérivée de chacun de ses éléments qui la composent. On calcule la dérivée de chaque élement
Pour calculer la dérivée d'un polynôme on calcule donc séparément la dérivée de chacun de ses éléments qui la composent. On calcule la dérivée de chaque élement 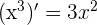


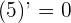 Il nous reste par la suite à simplement faire l'addition de l'ensemble des dérivées.
Il nous reste par la suite à simplement faire l'addition de l'ensemble des dérivées.
D'où 
f(x) étant un polynôme, elle est définie et dérivable sur R.De la même manière que l'on a fait précédemment, on calcule l'ensemble des dérivées unitaires de notre polynôme. 

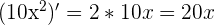 Il nous reste maintenant simplement à additionner les résultats de nos dérivées.
Il nous reste maintenant simplement à additionner les résultats de nos dérivées.
D'où 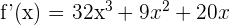
Pour calculer la dérivée de cette fonction, il existe 2 possibilités :
- 1. Développer la fonction puis calculer la dérivée du polynôme
- 2. Utiliser le modèle des opérations et dérivées en considérant la fonction avec le produit u*v
On va pour l'exemple utiliser les deux méthodes pour calculer cette dérivée en cours de maths terminale s .
- On développe la fonction f(x) :
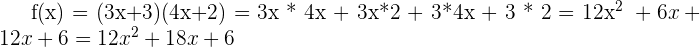 Une fois le développement effectué, bien que cela ne soit pas obligatoire, on peut factoriser notre fonction, on obtiendrait ainsi :
Une fois le développement effectué, bien que cela ne soit pas obligatoire, on peut factoriser notre fonction, on obtiendrait ainsi : 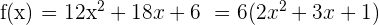 Maintenant que l'on a notre polynôme, il nous suffit de calculer la dérivée de chacun des éléments :
Maintenant que l'on a notre polynôme, il nous suffit de calculer la dérivée de chacun des éléments :  On obtient donc
On obtient donc 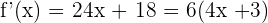 2. On utilise la formule dans notre tableau d'opérations et dérivées : On considère que la fonction f(x) est sous la forme f(x) = u*v avec u = 3x + 3 et v = 4x+2. On calcule la dérivée de u. u' = 3 + 0 = 3 On calcule la dérivée de v : v' = 4 + 0 = 4 Enfin d'après la tableau des opérations et dérivées, on sait que : (u*v)' = u'v + uv' Pour résumer on a u = 3x + 3, u' = 3, v = 4x+2 et v' = 4. Vous cherchez des cours de maths seconde ? On applique notre formule :
2. On utilise la formule dans notre tableau d'opérations et dérivées : On considère que la fonction f(x) est sous la forme f(x) = u*v avec u = 3x + 3 et v = 4x+2. On calcule la dérivée de u. u' = 3 + 0 = 3 On calcule la dérivée de v : v' = 4 + 0 = 4 Enfin d'après la tableau des opérations et dérivées, on sait que : (u*v)' = u'v + uv' Pour résumer on a u = 3x + 3, u' = 3, v = 4x+2 et v' = 4. Vous cherchez des cours de maths seconde ? On applique notre formule :  On retrouve bien le même résultat qu'avec la méthode 1.
On retrouve bien le même résultat qu'avec la méthode 1.
Pour trouver l'ensemble de définition de la fonction, il faut trouver la valeur de x pour laquelle le dénominateur est égal à 0. On doit donc résoudre l'équation suivante : 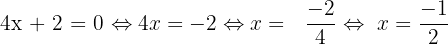 La fonction f(x) est donc définie et dérivable sur R{-1/2}. La fonction f(x) est sous la forme 1/u avec u = 4x+2. D'après le tableau ci-dessus, on sait que :
La fonction f(x) est donc définie et dérivable sur R{-1/2}. La fonction f(x) est sous la forme 1/u avec u = 4x+2. D'après le tableau ci-dessus, on sait que : 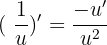 On calcule séparément u'. u' = 4. Enfin, on applique la formule :
On calcule séparément u'. u' = 4. Enfin, on applique la formule : 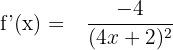
Comme pour la fonction précédente, on doit regarder dans un premier temps pour quelle valeur le dénominateur s'annule. Le dénominateur étant le même que dans la fonction précédente, on connait déjà la valeur (cours de maths 3ème). f(x) est définie et dérivable sur R{-1/2}. On constate ici que la fonction est sous le format u/v avec u = 3x+3 et v = 4x+2. On calcule les dérivées de u et v. u' =3 et v' =4 Il nous reste ensuite simplement à appliquer la formule : 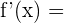
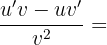
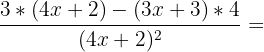
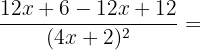
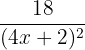
Pour déterminer l'ensemble de définition de la fonction, il faut connaitre la valeur pour laquelle le dénominateur s'annule. Il nous faut donc résoudre l'équation suivante : (4x+2)(2x+5) = 0 Pour résoudre cette équation, nous avons 2 possibilités. Néanmoins, par soucis de rapidité la première méthode sera préférée à la deuxième.
- 1. Le produit de deux éléments qui s'annulent veut dire que, soit le premier est nul, soit le deuxième élément est nul.
- 2. On développe l'équation et on résoud l'équation de 2nd degré.
1. Avec la méthode 1, on sait que si (4x+2)(2x+5) = 0 alors 4x +2 = 0 ou 2x+5 = 0. D'où x1 = -1/2 et x2 = -5/2 2. Avec la méthode 2, on développe notre équation  On obtient l'équation du second degré suivante :
On obtient l'équation du second degré suivante : 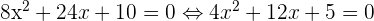 On calcule le déterminant :
On calcule le déterminant : 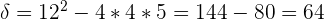 Le discriminant étant positif, on obtient les valeurs suivantes :
Le discriminant étant positif, on obtient les valeurs suivantes : 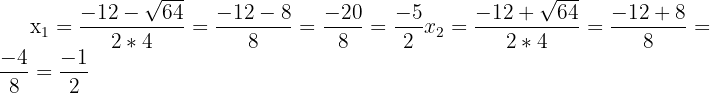 On retrouve bien les mêmes résultats qu'avec la méthode 1. Par conséquent, f(x) est définie et dérivable sur R{-1/2;-5/2}. Cette dernière fonction est plus compliquée à dériver car il faut prendre en compte plusieurs facteurs. On peut transformer la fonction comme suit :
On retrouve bien les mêmes résultats qu'avec la méthode 1. Par conséquent, f(x) est définie et dérivable sur R{-1/2;-5/2}. Cette dernière fonction est plus compliquée à dériver car il faut prendre en compte plusieurs facteurs. On peut transformer la fonction comme suit : 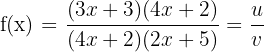 avec u = (3x + 3)(4x+2) et v = (4x + 2)(2x+5) Pour calculer la dérivée de u, on la décompose à nouveau comme suit : u = (3x + 3)(4x+2) = a*b avec a = 3x + 3 et b = 4x+2 On calcule donc les dérivées de a et b : a' = 3 et b' = 4. On obtient donc : u' = a'b + ab' = 3(4x+2) + (3x+3)*4 = 12x + 6 + 12x + 12 = 24x + 18 De la même manière on décompose v: v = (4x + 2)(2x+5) = s*t avec s = 4x+2 et t = 2x+5 On calcule les dérivées de s et t : s' = 4 et t'= 2 Enfin on calcule v' : v' = s't + st' = 4(2x+5) + (4x+2)*2 = 8x + 20 + 8x + 4 = 16x + 24 On a : u = (3x + 3)(4x+2) , u' = 24x + 18 et v = (4x + 2)(2x+5) , v' = 16x + 24 On peut donc calculer la dérivée de f :
avec u = (3x + 3)(4x+2) et v = (4x + 2)(2x+5) Pour calculer la dérivée de u, on la décompose à nouveau comme suit : u = (3x + 3)(4x+2) = a*b avec a = 3x + 3 et b = 4x+2 On calcule donc les dérivées de a et b : a' = 3 et b' = 4. On obtient donc : u' = a'b + ab' = 3(4x+2) + (3x+3)*4 = 12x + 6 + 12x + 12 = 24x + 18 De la même manière on décompose v: v = (4x + 2)(2x+5) = s*t avec s = 4x+2 et t = 2x+5 On calcule les dérivées de s et t : s' = 4 et t'= 2 Enfin on calcule v' : v' = s't + st' = 4(2x+5) + (4x+2)*2 = 8x + 20 + 8x + 4 = 16x + 24 On a : u = (3x + 3)(4x+2) , u' = 24x + 18 et v = (4x + 2)(2x+5) , v' = 16x + 24 On peut donc calculer la dérivée de f : 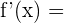
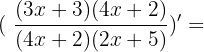
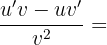
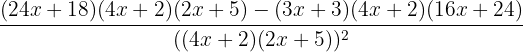












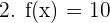
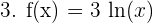
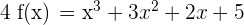
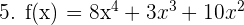
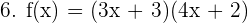
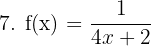
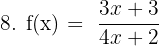
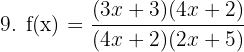
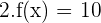
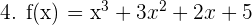
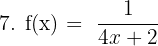








Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !