Chapitres
? Les équations du second degré prennent la forme ax² + bx + c = 0, où x est inconnu. Elles peuvent être résolues en utilisant la formule quadratique, fournissant deux solutions potentielles pour x. Ces équations apparaissent fréquemment dans divers domaines mathématiques et physiques pour modéliser des relations quadratiques.
Voici tout ce qu'il faut savoir sur ces équations ✍️
Quelques propriétés ?
- Propriété 1 : Si l'équation admet deux racines
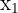et 
(donc son discriminant Δ > 0) alors :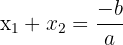 
et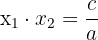 
- Propriété 2 : Si l'équation admet deux racines x1 et x2 (donc son discriminant Δ = 0), alors : P(x) = a(x - x1)(x - x2).
- Propriété 3 : Si Δ < 0, P(x) a le signe de a pour tout x, Si Δ = 0, P(x) a le signe de a pour tout x différent de -b/2a, Si Δ > 0, P(x) a le signe de a à l'extérieur des racines et le signe de (- a) entre les racines.
? Les équations du second degré, de la forme ax² + bx + c = 0, présentent plusieurs propriétés clés. Elles peuvent avoir :
Deux solutions réelles
Une solution double
Deux solutions complexes
La discriminante (Δ = b² - 4ac) dicte la nature des solutions :
- Δ > 0 pour deux solutions réelles
- Δ = 0 pour une solution double
- Δ < 0 pour deux solutions complexes
La forme canonique (a(x - h)² + k) permet d'analyser le sommet de la parabole associée. La résolution peut se faire à l'aide de la formule quadratique : x = (-b ± √Δ) / 2a.
Résoudre une équation du second degré ?
? Une équation du second degré est de la forme : P(x) = ax² + bx + c, avec a, b et c réels. Pour résoudre l'équation ax² + bx + c = 0, il faut suivre le modèle suivant :
- Étape 1 : Calcul du discriminant Δ = b² - 4ac.
- Étape 2 : Analyse du discriminant
- Si Δ < 0 : Pas de solution à l'équation ;
- Si Δ = 0 : Une seule solution S = -b/2a ;
- Si Δ > 0 : Deux solutions à l'équation S = {(-b-racine(Δ))/2a, (-b+racine(Δ))/2a}.
En pratique : cas concret
Considérons l'équation x2−3x−10= 0
- Forme canonique : x2−3x + 2x −10= 0
- Calcul du discriminant : Δ= (−3)2 − 4(1)(−10) = 49
- Nature des solutions : Δ > 0, deux solutions réelles
- Formule quadratique :
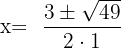
Les solutions sont:
Vous avez aimé cet article ? Notez-le !
Loading...
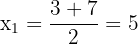
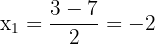
Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Très merveilleuse les mathématiques vraiment j’aimerais être forte en maths
que vient faire la formule du phénol au milieu des calculs???pour faire plus savant ?
Bonjour ! Pour un soutien sur mesure, découvrez nos formateurs sur Superprof. Ils sont prêts à vous aider selon vos besoins pour atteindre vos objectifs. Contactez-les pour commencer votre parcours personnalisé ! Bonne journée. :)
Aide moi comment résoudre ax2+bx+c=0 en utilisant la méthode de résolution par factorisation
Bonjour ! Rencontrez nos formateurs qualifiés sur Superprof, qui sont là pour vous proposer un soutien personnalisé. Excellente journée à vous ! :)
Quel est la formule de la méthode d’identification aidez moi
J’adore 👍 cette article.
Aidé moi à traité certains exercices
4×2-7x=0