Chapitres
🤓 Les relations fondamentales en trigonométrie sont des équations qui définissent les liens entre les côtés et les angles d'un triangle, essentielles pour résoudre des problèmes géométriques et analytiques. Elles sont basées sur les fonctions trigonométriques telles que le sinus, le cosinus et la tangente.
👷♂️ Ces relations sont cruciales pour résoudre des problèmes trigonométriques dans divers domaines tels que la géométrie, la physique, l'ingénierie et les mathématiques appliquées.
Voici toutes les formules à connaître !
Généralités sur la trigonométrie et ses formules ✅
Relations fondamentales
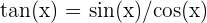
Cette formule définit la tangente d'un angle en termes du sinus et du cosinus de cet angle. En d'autres termes, la tangente d'un angle est égale au rapport du sinus de l'angle sur son cosinus.
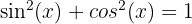
👌 Il s'agit de l'identité trigonométrique la plus célèbre, connue sous le nom "d'identité pythagoricienne". Elle exprime que le carré du sinus d'un angle plus le carré du cosinus de cet angle est égal à 1. C'est une conséquence directe du théorème de Pythagore appliqué au cercle unité.
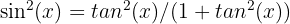
Cette formule exprime le carré du sinus d'un angle en termes du carré de la tangente de cet angle. Elle montre que le carré du sinus est égal au carré de la tangente divisé par 1 plus le carré de la tangente.
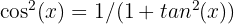
🙇♂️ Cette formule exprime le carré du cosinus d'un angle en termes de la tangente de cet angle. Elle montre que le carré du cosinus est égal à 1 divisé par 1 plus le carré de la tangente.
Transformations remarquables
👉 Parmi les transformations remarquables en trigonométrie, on retrouve les 5 éléments suivants :
- Décalage horizontal :
- Pour les fonctions trigonométriques, un décalage horizontal de a unités est représenté par
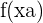. - Par exemple,
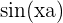décale la fonction sinus de a unités vers la droite.
- Pour les fonctions trigonométriques, un décalage horizontal de a unités est représenté par
- Décalage vertical :
- Un décalage vertical de b unités pour une fonction trigonométrique est représenté par
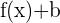. - Par exemple,
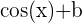décale la fonction cosinus de b unités vers le haut.
- Un décalage vertical de b unités pour une fonction trigonométrique est représenté par
- Amplitude :
- L'amplitude d'une fonction trigonométrique détermine l'étirement vertical ou la compression de la fonction.
- Pour
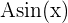ou 
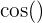, A∣ est l'amplitude de la fonction.
- Période :
- La période P d'une fonction trigonométrique contrôle la longueur de son cycle.
- Pour
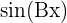ou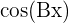 
, la période est 
.
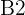- Phase :
- La phase C contrôle le décalage horizontal (ou le retard) d'un cycle.
- Pour
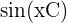ou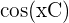 
, la phase est C.
📝 Voici quelques formules incontournables pour parler des transformations remarquables :
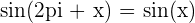
Cette formule exprime que le sinus d'un angle décalé de 2𝜋2π radians est égal au sinus de cet angle initial. En d'autres termes, le sinus est une fonction périodique avec une période de 2𝜋2π radians.
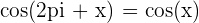
De manière similaire à la première formule, cette propriété indique que le cosinus d'un angle décalé de 2𝜋2π radians est égal au cosinus de l'angle initial. Le cosinus est également une fonction périodique avec une période de 2𝜋2π radians.
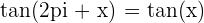
Cette formule signifie que la tangente d'un angle décalé de 2𝜋2π radians est égale à la tangente de cet angle initial. Tout comme le sinus et le cosinus, la tangente est une fonction périodique avec une période de 2𝜋2π radians.
Équations trigonométriques
👨🏫 Ces équations trigonométriques sont basées sur les propriétés de périodicité des fonctions trigonométriques.
Pour l'équation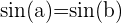 
- Lorsque les sinus sont égaux mais de signes opposés, cela signifie que les angles a et b sont à une distance égale d'un multiple de π radians.
- Donc, 𝑎a peut être b+2k où k est un nombre entier, car ajouter un multiple de 2π radians à un angle ne change pas son sinus.
- De même, 𝑎a peut aussi être −b+2k, car soustraire b et ajouter un multiple de 2π radians donne le même sinus.
Pour l'équation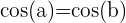 
- De manière similaire à l'équation précédente, lorsque les cosinus sont égaux mais de signes opposés, cela signifie que les angles a et b sont à une distance égale d'un multiple de π radians.
- Donc, a peut être b+2k où k est un nombre entier, car ajouter un multiple de 2π radians à un angle ne change pas son cosinus.
- De même, a peut aussi être −b+2k, car soustraire b et ajouter un multiple de 2π radians donne le même cosinus.
Pour l'équation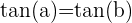 
- Lorsque les tangentes sont égales mais de signes opposés, cela signifie que les angles a et b sont à une distance égale d'un multiple de π radians.
- Donc, a peut être b+k où k est un nombre entier, car ajouter un multiple de π radians à un angle ne change pas sa tangente.
Formules d'addition 🤓
Formules d'addition pour le sinus
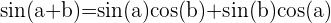
Cette formule exprime le sinus de la somme de deux angles a et b en termes des sinus et cosinus des angles individuels.
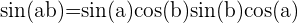
De manière similaire à la première formule, cette formule exprime le sinus de la différence de deux angles a et b.
Formules d'addition pour le cosinus
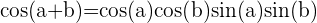
Cette formule exprime le cosinus de la somme de deux angles a et b en termes des cosinus et sinus des angles individuels.
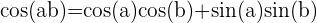
Tout comme indiqué précédemment, cette formule exprime le cosinus de la différence de deux angles a et b.
Formules de multiplication 🤔
💪 La formule de Moivre est une identité fondamentale en trigonométrie qui permet d'élever un nombre complexe à une puissance entière. Elle établit une relation entre les coordonnées polaires et rectangulaires d'un nombre complexe élevé à une puissance entière.
Formule de Moivre
Voici la forme générale de la formule de Moivre :
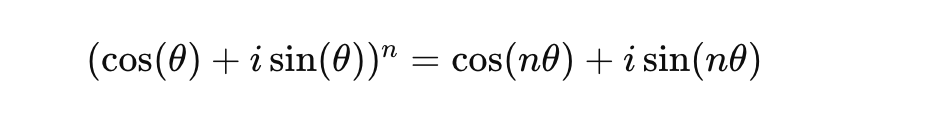
où :
- n est un entier positif ou négatif
- θ est l'argument du nombre complexe
- i est l'unité imaginaire
👉 Cette formule découle de l'expression du nombre complexe sous sa forme polaire :
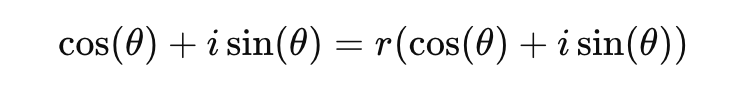
où :
- r est le module du nombre complexe
- Ce qui donne la forme rectangulaire du résultat de la formule de Moivre.
Elle permet notamment de calculer rapidement les racines n-èmes d'un nombre complexe et de simplifier les expressions trigonométriques impliquant des puissances élevées.
Vous avez aimé cet article ? Notez-le !
Loading...
Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
3sin,(π+x) c’est t’il la mm formule que celle de son(π+x) ?
Bonjour ! Pour aller plus loin, n’hésitez pas de solliciter nos professeurs particuliers sur Superprof pour une aide personnalisée et plus poussée. Bonne journée ! 🙂
Merci c’est parfait, Bonne continuation…
intéressant !!
avec des exemples ce serait mieux
OUI tres utile
lequel est le bon svp
Pour tout nombre réel x, cos(x+3pi)=
– cos(x)
– ─ cos(x)
– sin(x)
Vous écrivez une grossière erreur un peu plus haut : Sinus ( x) + cosinus (x) = 1 est faut !!
Revoyez le théorème de Pythagore!
Sinus carré (x) + cosinus carré ( x) = 1
Le superprof ferait bien de retourner à l’école…
Bonjour Pierre, merci pour votre commentaire qui nous a permis d’identifier une erreur d’affichage de LaTex sur notre site. Il ne s’agit donc pas d’un besoin de retourner à l’école pour Superprof :), et ni pour Thomas. Nous apprécions votre contributions, n’hésitez pas à nous écrire si jamais vous observez d’autres anomalies sur nos pages. Notre but est de partager le savoir sans erreur humaine ou pas! Bon été à vous et bonne rentrée aussi
Je n’est que deux choses a dire: « Merci » et « Continue ». Cette fiche est geniale, tres claire, simple et surtout concise. encore une fois merci!
Je met 5, franchement bien résumé, clair et précis, une fiche comme celle là on met 3h à la faire tu m’a fait gagne run temps précieux! merci!