Chapitres

Introduction
Les suites représentent un chapitre indispensable du programme de 1ère S. Suite de Fibonacci, de Cauchy ou encore de Syracuse, les suites sont très étudiées en mathématiques et à très haut niveau. Il est donc nécessaire de connaître les bases.
Définition d'une suite

Une suite est une famille d'éléments qu'on appelle des "termes". Dans ce cours, nous étudions les suites numériques, que l'on peut voir comme des fonctions de N (ensemble des entiers naturels) dans R (ensemble des nombres réels). Les termes de la suite sont donc des réels. Une suite est notée 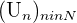 Au lycée, on la note plus simplement
Au lycée, on la note plus simplement 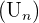 où les nombres réels
où les nombres réels 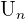 sont les termes de la suite. La plupart du temps, une suite a pour premier terme
sont les termes de la suite. La plupart du temps, une suite a pour premier terme 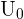 ou
ou 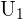 Soit
Soit 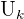 un des termes de la suites. On dit que k est l'indice ou le rang. Il existe deux manières de définir une suite :
un des termes de la suites. On dit que k est l'indice ou le rang. Il existe deux manières de définir une suite :
- De manière explicite : on définit la suite en fonction de n. On a donc

Par exemple, 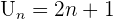 Ici, le premier terme est
Ici, le premier terme est 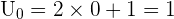 C'est le terme de rang 0. Si l'on veut calculer
C'est le terme de rang 0. Si l'on veut calculer  il suffit de remplacer n par 5 :
il suffit de remplacer n par 5 : 
- Par récurrence : on définit chaque terme par rapport au terme qui le précède. C'est à dire
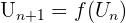 ou
ou 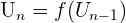
Par exemple : 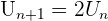 avec
avec 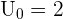 Lorsque l'on définit une suite par récurrence, il est nécessaire de donner le premier terme. Pour obtenir un des termes de la suite, on est obligé de calculer tous les termes précédents. Si l'on veut calculer
Lorsque l'on définit une suite par récurrence, il est nécessaire de donner le premier terme. Pour obtenir un des termes de la suite, on est obligé de calculer tous les termes précédents. Si l'on veut calculer  il nous faut calculer
il nous faut calculer 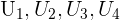 Dans notre exemple on obtient :
Dans notre exemple on obtient :
| U0 | U1 | U2 | U3 | U4 | U5 |
|---|---|---|---|---|---|
| 2 | 2xU0=4 | 2xU1=8 | 2xU2=16 | 2xU3=32 | 2xU4=64 |
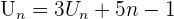
Variation d'une suite
En cours de math, une suite est croissante si pour tout entier naturel n sur lequel elle est définit on a  Elle est strictement croissante si
Elle est strictement croissante si  Inversement, une suite est décroissante si pour tout entier naturel n sur lequel elle est définit on a
Inversement, une suite est décroissante si pour tout entier naturel n sur lequel elle est définit on a 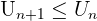 Elle est strictement décroissante si
Elle est strictement décroissante si 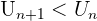 On dit qu'une suite est monotone si elle est strictement croissante ou strictement décroissante. Une suite est dite constante si
On dit qu'une suite est monotone si elle est strictement croissante ou strictement décroissante. Une suite est dite constante si  pour tout entier naturel n sur lequel elle est définit. Bien-sur, il existe des suites qui ne sont ni croissantes, ni décroissantes ni constantes. Par exemple, la suite
pour tout entier naturel n sur lequel elle est définit. Bien-sur, il existe des suites qui ne sont ni croissantes, ni décroissantes ni constantes. Par exemple, la suite 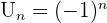 Les termes de la suite valent 1,-1,1,-1, etc... C'est une suite alternée. Afin d'étudier le sens de variation d'une suite on étudie le signe de
Les termes de la suite valent 1,-1,1,-1, etc... C'est une suite alternée. Afin d'étudier le sens de variation d'une suite on étudie le signe de  Si cette différence est positive, alors la suite Un est croissante. Si le résultat est négatif, alors la suite est décroissante. Si la différence vaut 0, la suite est constante. Étudions un exemple :
Si cette différence est positive, alors la suite Un est croissante. Si le résultat est négatif, alors la suite est décroissante. Si la différence vaut 0, la suite est constante. Étudions un exemple : 
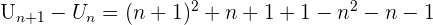
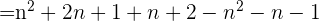
 Comme n est positif, 2n+2 est positif. Donc la suite Un est croissante. Pour étudier le sens de variation il est aussi possible d'étudier le rapport
Comme n est positif, 2n+2 est positif. Donc la suite Un est croissante. Pour étudier le sens de variation il est aussi possible d'étudier le rapport 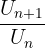 Si le rapport est supérieur à 1, la suite est croissante. Si le rapport est inférieur à 1, la suite est décroissante. Enfin, si le rapport vaut 1, la suite est constante. Cette méthode, contrairement à la première, n'est pas toujours probante mais elle est plus rapide lorsque les calculs ne concerne que des multiplications, divisions ou puissances.
Si le rapport est supérieur à 1, la suite est croissante. Si le rapport est inférieur à 1, la suite est décroissante. Enfin, si le rapport vaut 1, la suite est constante. Cette méthode, contrairement à la première, n'est pas toujours probante mais elle est plus rapide lorsque les calculs ne concerne que des multiplications, divisions ou puissances.
Convergence d'une suite

On dit d'une suite est convergente si elle admet une limite, c'est à dire s'il existe un nombre réel l vers lequel tend Un quand n tend vers l'infini. On note 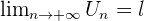 Par exemple, la suite
Par exemple, la suite 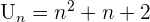 tend vers l'infini quand n tend vers l'infini. Donc la suite ne converge pas. Elle diverge. Regardons la suite
tend vers l'infini quand n tend vers l'infini. Donc la suite ne converge pas. Elle diverge. Regardons la suite 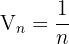 Quand n tend vers l'infini, la suite tend vers 0. Donc la suite converge vers l=0. La suite Un est dite majorée s'il existe un M tel que
Quand n tend vers l'infini, la suite tend vers 0. Donc la suite converge vers l=0. La suite Un est dite majorée s'il existe un M tel que 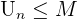 quelque soit n un entier naturel. Si la suite Un est croissante et majorée alors la suite est convergente. Une suite croissante non majorée est divergente et tend vers l'infini. La suite Un est dite minorée s'il existe un m tel que
quelque soit n un entier naturel. Si la suite Un est croissante et majorée alors la suite est convergente. Une suite croissante non majorée est divergente et tend vers l'infini. La suite Un est dite minorée s'il existe un m tel que  quelque soit n. Si la suite Un est décroissante et minorée, alors la suite est convergente. Une suite décroissante non minorée est divergente et tend vers
quelque soit n. Si la suite Un est décroissante et minorée, alors la suite est convergente. Une suite décroissante non minorée est divergente et tend vers  .
.
Comment prendre des cours de maths 3eme ?
Représentation graphique d'une suite
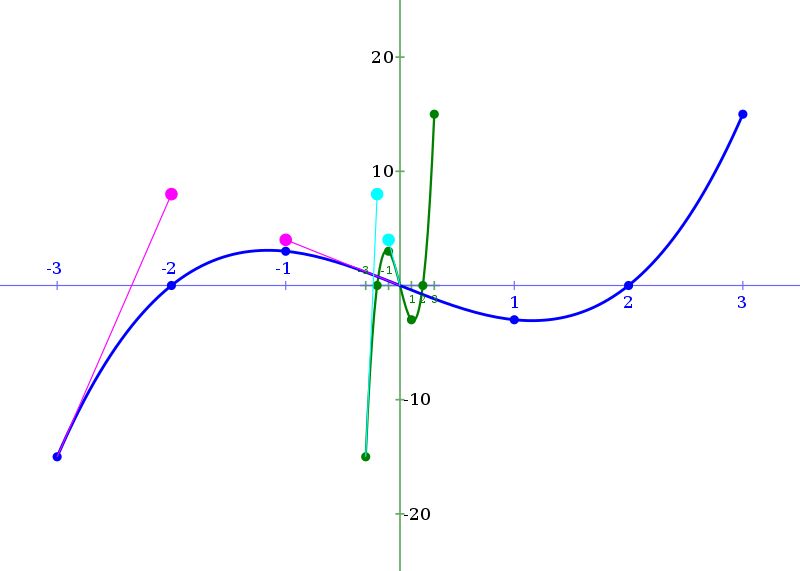
Il y a différentes manières pour représenter graphiquement une suite. La première est de calculer les termes de la suite un par un puis de les placer dans un repère. Lorsque l'on a une suite définie explicitement, il est possible de tracer la fonction f(n). Les différents termes de la suite correspondent aux points de la fonction ayant une valeur entière et positive en abscisse. Traçons par exemple 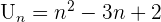 Les premiers termes de la suite correspondent aux points A,B,C,D et E. Ici
Les premiers termes de la suite correspondent aux points A,B,C,D et E. Ici 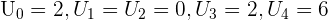

Enfin, lorsque l'on doit tracer une suite définie par récurrence, on passe par plusieurs étapes. On a 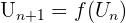 On commence par tracer la fonction f dans un repère ainsi que la droite y=x. On peut ensuite placer le point (U0,0). Ensuite, on trace la droite verticale partant de ce point. Son intersection avec la courbe f nous donne le point A, qui a pour ordonnée U1. On reporte U1 sur l'axe des abscisses grâce à la droite x=y. De cette façon on peut réitérer la méthode pour avoir les termes suivants. Étudions par exemple
On commence par tracer la fonction f dans un repère ainsi que la droite y=x. On peut ensuite placer le point (U0,0). Ensuite, on trace la droite verticale partant de ce point. Son intersection avec la courbe f nous donne le point A, qui a pour ordonnée U1. On reporte U1 sur l'axe des abscisses grâce à la droite x=y. De cette façon on peut réitérer la méthode pour avoir les termes suivants. Étudions par exemple 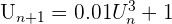 avec U0=5. On trace la fonction
avec U0=5. On trace la fonction  et la droite y=x. On place le point (U0,0) puis on applique la méthode énoncée ci-dessus.
et la droite y=x. On place le point (U0,0) puis on applique la méthode énoncée ci-dessus.
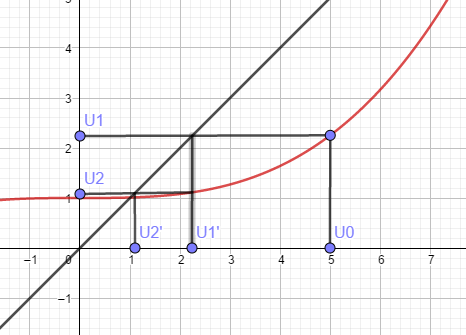
On vérifie en calculant les premiers termes :
| U0 | U1 | U2 | U3 |
|---|---|---|---|
| 5 | 0.01x5x5x5+1=2.25 | 0.01x2.25x2.25x2.25+1=1.114 | 0.01xU2xU2xU2+1=1 |
Suite arithmétique
Une suite arithmétique est une suite de la forme 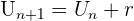 où r est un réel. r est appelé la raison de la suite Un. Par exemple,
où r est un réel. r est appelé la raison de la suite Un. Par exemple, 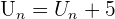 avec
avec 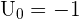 Une suite arithmétique peut aussi s'écrire de façon explicite :
Une suite arithmétique peut aussi s'écrire de façon explicite :  Par exemple, la suite
Par exemple, la suite 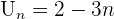 est arithmétique. Ainsi, lorsque l'on représente graphiquement les termes de la suite, on observe que les points sont alignés. Dans l'exemple précédent, on obtient
est arithmétique. Ainsi, lorsque l'on représente graphiquement les termes de la suite, on observe que les points sont alignés. Dans l'exemple précédent, on obtient 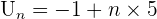 Pour écrire la suite de façon explicite, il suffit de connaitre un terme, et pas forcément celui de rang 0. Supposons qu'on connait le terme Uk.
Pour écrire la suite de façon explicite, il suffit de connaitre un terme, et pas forcément celui de rang 0. Supposons qu'on connait le terme Uk.  Lorsque l'on calcule la différence
Lorsque l'on calcule la différence  on obtient pour résultat la raison r. Ainsi, pour prouver qu'une suite est arithmétique, on calcule cette différence. Si elle est égale à une constante réelle, alors la suite est arithmétique de raison cette constante. De cette façon : Si r>0, la suite est croissante. Si r<0 la suite est décroissante. Si r=0, la suite est constante. Il est possible de calculer la somme des termes d'une suite arithmétique avec une formule simple :
on obtient pour résultat la raison r. Ainsi, pour prouver qu'une suite est arithmétique, on calcule cette différence. Si elle est égale à une constante réelle, alors la suite est arithmétique de raison cette constante. De cette façon : Si r>0, la suite est croissante. Si r<0 la suite est décroissante. Si r=0, la suite est constante. Il est possible de calculer la somme des termes d'une suite arithmétique avec une formule simple : 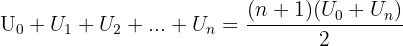 Si l'on ne commence pas la somme au premier terme mais au p-ième terme, on utilise :
Si l'on ne commence pas la somme au premier terme mais au p-ième terme, on utilise : 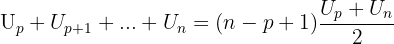 De cette façon,
De cette façon, 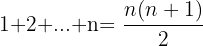
Suite géométrique

Une suite géométrique est une suite de la forme 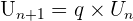 où q est un nombre réel. q est appelé la raison de la suite. Par exemple,
où q est un nombre réel. q est appelé la raison de la suite. Par exemple, 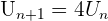 avec
avec 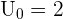 est une suite géométrique. La forme explicite de la suite est de la forme
est une suite géométrique. La forme explicite de la suite est de la forme 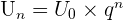 Dans notre exemple, on obtient
Dans notre exemple, on obtient 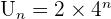 Dans le cas général, lorsque l'on connait un des termes de la suite ainsi que son expression sous forme de récurrence on a
Dans le cas général, lorsque l'on connait un des termes de la suite ainsi que son expression sous forme de récurrence on a 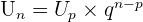 Faisons un exercice. On souhaite exprimer Un en fonction de n en partant de
Faisons un exercice. On souhaite exprimer Un en fonction de n en partant de  avec
avec 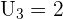 On obtient
On obtient 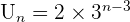 En sachant que pour tout m on a
En sachant que pour tout m on a 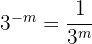 On peut vérifier que les deux formules nous permettent d'obtenir les mêmes résultats :
On peut vérifier que les deux formules nous permettent d'obtenir les mêmes résultats :
| Un+1=f(Un) | U1=U2/3=2/9 | U2=U3/3=2/3 | U3=2 | U4=3xU3=6 | U5=3xU4=18 |
|---|---|---|---|---|---|
| Un=f(n) | U1=2x1/(3x3)=2/9 | U2=2x1/3=2/3 | U3=2 | U4=2X3+6 | U5=2x3x3=18 |
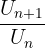 est égal à une constante réelle qui correspondra à la raison q. Suite à ça, on en déduit les variations de la suite
est égal à une constante réelle qui correspondra à la raison q. Suite à ça, on en déduit les variations de la suite 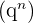 Si q>1, la suite est strictement croissante. Si q=1, la suite est constante. Si 0<q<1, la suite est strictement décroissante. Il est possible de calculer la somme des premiers termes d'une suite géométrique.
Si q>1, la suite est strictement croissante. Si q=1, la suite est constante. Si 0<q<1, la suite est strictement décroissante. Il est possible de calculer la somme des premiers termes d'une suite géométrique. 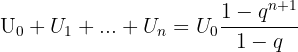 Si l'on ne souhaite pas commencer au premier terme mais au p-ième terme, on a
Si l'on ne souhaite pas commencer au premier terme mais au p-ième terme, on a 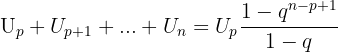 En particulier, la somme des puissances d'un nombre donne :
En particulier, la somme des puissances d'un nombre donne : 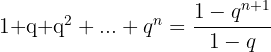
Résumer avec l'IA :




















Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Très bonne idée la partie à surligner pour avoir la solution !
Aidez-moi à comprendre les mathématiques
Bonjour, nous vous invitons à contacter un de nos professeurs particuliers. Il pourra vous donner des cours et exercices personnalisés en fonction de vos besoins. Belle journée !