Chapitres

I/ La bobine en convention récepteur
A) Représentation symbolique
Une bobine est constituée d'un enroulement serré de fil conducteur enrobé d'un matériau isolant. Ce fil conducteur présente le plus souvent une résistance r de faible valeur.
Une bobine de résistance r est équivalente à l'association en série d'une bobine de résistance nulle et d'un conducteur ohmique de résistance r, nous utiliserons la représentation symbolique suivante:
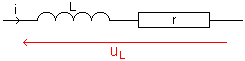
B) Etude expérimentale
On réalise le montage ci-dessous.
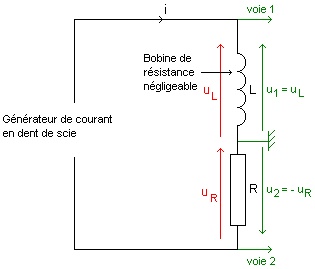
L'ordinateur permet de tracer les courbes uL=f(t) et i=f(t) (car 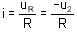
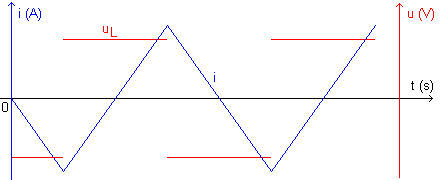
C) Inductance de la bobine
Pendant une demi-période le courant i est de la forme i=a.t+b et de ce fait, 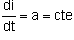
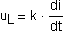
| avec | | uL: tension aux bournes de la bobine en volts (V). | |
| L: inductance de la bobine en henrys (H). | ||||
| di/dt: dérivée par rapport au temps de l'intensité du courant traversant la bobine en ampères par seconde (A.s-1). |
D) Tension aux bornes de la bobine
Si la résistance de la bobine n'est pas négligeable, celle-ci peut-être considérée comme l'association série d'un conducteur ohmique et d'une bobine de résistance nulle.
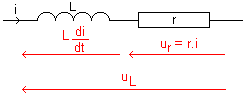
La tension aux bornes de la bobine s'écrit alors:
| avec | | uL: tension aux bornes de la bobine en volts (V). | |
| L: inductance de la bobine en henrys (H). | ||||
| r: résistance de la bobine en ohms (W). | ||||
| i: intensité du courant traversant la bobine en ampères (A). | ||||
| di/dt: dérivée par rapport au temps de l'intensité du courant traversant la bobine en ampères par seconde (A.s-1). |
Remarques
- Dans le cas où la bobine est une inductance pure, sa résistance est nulle et la tension à ses bornes s'écrit
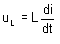
- En régime permanent, le courant est constant (i=cte), la tension aux bornes de la bobine s'écrit uL=ri: la bobine se comporte comme un conducteur ohmique.
II. Réponse d'un dipôle RL à un échelon de tension
A) Etude expérimentale
On réalise le montage ci-contre:
L'ordinateur permet de tracer la courbe i=f(t) (car 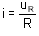
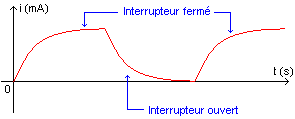
Interprétation:
- Interrupteur fermé: Le courant s'installe progressivement: la bobine s'oppose à l'apparition de celui-ci.
- Interrupteur ouvert: Le courant diminue progressivement: la bobine s'oppose à la disparition de celui-ci.
Conclusion: Une bobine s'oppose aux variations de l'intensité du courant dans le circuit où elle se trouve.
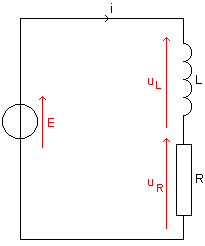

a. Equation différentielle
D'après la loi d'additivité des tensions:
| uR + uL = E | => | => | |
b. Solution de l'équation différentielle
Remarque préalable: en régime permanent, le courant est constant.
| i = cte | => | => |
Vérifions que i=A+Be-t/t est solution de l'équation différentielle.
di/dt = -B/t.e-t/t. L'équation différentielle s'écrit alors:
| A+Be-t/t + L/R.(-B/t.e-t/t) = E/R | => | A + B.(1 - L/Rt).e-t/t = E/R |
Cette équation est vérifiée quelquesoit le paramètre t, d'où le système:
| A = E/R 1 - L/Rt = 0 | => | A = E/R t = L/R |
On en déduit que l'intensité du courant s'écrit i = E/R + B.e-t/t avec t = L/R.
| D'autre part, à t = 0, i = 0 | => | 0 = E/R + B.e0 | |
| => | B = -E/R | ||
| => | i = E/R - E/R.e-t/t | ||
| => |
|
Définition: La grandeur t=L/R est appelée constante de temps du circuit. Son unité est la seconde (s).
Remarque: analyse dimentionnelle
| uR = R.i | => | [R] = [U].[I]-1 | ||||||||||
| uL = L.di/dt | => | [L] = [U].[T].[I]-1 | ||||||||||
| => |
| ||||||||||
| => | [L/R] = [T] |
L/R est homogène à un temps.
Remarque: La constante de temps fournit un ordre de grandeur de la durée de la réponse d'un circuit RL.
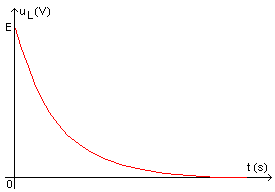

| uL = L.di/dt | => | uL = L.E/R.(1/t.e-t/t) avec t=L/R | |
| => |
|
Remarque: Détermination de uL à partir de la loi des tensions:
| uL + uR = E | => | uL = E - uR |
| => | uL = E - R.i | |
| => | uL = E - R.E/R.(1 - e-t/t) | |
| => | uL = E.e-t/t |
D) Détermination de la constante de temps
- Après une durée t, l'intensité est égale à 63% de sa valeur maximale.
- Après une durée 5t, l'intensité est égale à 99% de sa valeur maximale.
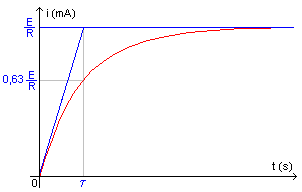 | 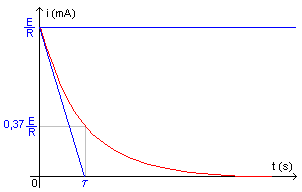 |
| Apparition du courant lors de la fermeture du circuit | Disparition du courant lors de l'ouverture du circuit |
III/ Énergie emmagasinée dans une bobine
Une bobine d'inductance L traversée par un courant i emmagasine l'énergie magnétique:
| avec | | EL: énergie emmagasinée par la bobine en joules (J). | |
| L: inductance de la bobine en henrys (H). | ||||
| i: intensité du courant traversant la bobine en ampères (A). |
Résumer avec l'IA :











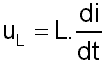
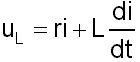
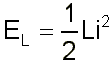












Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
Très bien merci beaucoup et j’éspaire vous contenue et ajoutez par exemple le cours de svt