Chapitres
Les référentiels et la trajectoire : cadre de l'étude
Le référentiel, l'espace et le temps
Un référentiel est un solide par rapport auquel on étudie un mouvement. Le choix du référentiel est crucial car il détermine la description du mouvement. On utilise souvent le solide terre comme référentiel.
Le référentiel géocentrique (centré sur la terre et construit à partir de trois étoiles lointaines qui paraissent fixes) est utilisé pour étudier le mouvement des satellites terrestres.
Le référentiel héliocentrique (centré sur le soleil et construit à partir de trois autres étoiles) est utilisé pour étudier les voyages interplanétaires ou le mouvement des planètes autour du soleil.
Un repère d'espace orthonormé, lié à un référentiel, est un système d'axes orthogonaux et normés, muni d'une origine O. Dans ce repère, on peut exprimer les coordonnées du mobile ponctuel étudié.
La trajectoire d'un mobile ponctuel est constituée par l'ensemble des positions successives occupées par le mobile au cours du temps. Elle dépend du référentiel choisi. Elle peut être rectiligne (une droite), circulaire (un arc de cercle) ou curviligne (une courbe quelconque).
| Référentiel | Solide de Référence (Centre) | Usage Principal | Conditions pour être Galiléen |
|---|---|---|---|
| Terrestre | La terre | Étude des mouvements à la surface du globe. | Durée de l'étude très courte (quelques minutes). |
| Géocentrique | Le centre de la terre | Étude des mouvements des satellites terrestres. | Durée de l'étude courte (quelques heures). |
| Héliocentrique | Le centre du soleil | Étude des planètes et des voyages interplanétaires. | Mouvements considérés comme longs (l'impact de la rotation du soleil est négligeable). |
| Galiléen | Tout solide en translation rectiligne uniforme par rapport à un autre référentiel galiléen. | Référentiel où le principe d'inertie est vérifié. | La somme des forces extérieures est nulle. |
Vitesse et mouvement
Pour calculer la vitesse moyenne (v en m/s) entre deux instants d'un solide, on utilise la formule suivante : vitesse moyenne = distance parcourue (m) / durée du parcours (s).
Le vecteur vitesse instantanée est la dérivée du vecteur position par rapport au temps. Ce vecteur est porté par la tangente à la trajectoire à la date considérée et a toujours le sens du mouvement.
Les lois de newton : définitions fondamentales
Première loi de newton : le principe d'inertie
Aussi appelée principe d'inertie ou loi d'inertie, elle s'énonce ainsi :
Un système isolé ou pseudo-isolé initialement au repos ou en mouvement rectiligne uniforme demeure dans son état.
Un système est isolé s'il n'est soumis à aucune force.
Un système est pseudo isolé si la somme vectorielle des forces extérieures appliquées à ce système est nulle :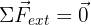 
.
Dans un référentiel galiléen, si la somme vectorielle des forces extérieures qui s'exercent sur un système est nulle, alors le vecteur vitesse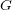 
du centre d'inertie du système est constant (et réciproquement). Un corps peut donc se déplacer même si la somme des forces est nulle, s'il est en mouvement rectiligne uniforme.
Le référentiel galiléen
On appelle référentiel galiléen tout référentiel au sein duquel le principe d'inertie est vérifié. Bien qu'il n'existe aucun référentiel galiléen au sens strict, certains référentiels usuels peuvent l'être sous certaines conditions :
Le référentiel terrestre est considéré galiléen si l'étude n'excède pas quelques minutes.
Le référentiel géocentrique est galiléen si l'étude n'excède pas quelques heures.
Le référentiel héliocentrique est galiléen car l'impact du mouvement de rotation du soleil au sein de la galaxie est négligeable.
Deuxième loi de newton : relation fondamentale de la dynamique
Dans un référentiel galiléen, si la somme vectorielle des forces appliquées à un solide est non nulle, alors le vecteur vitesse du centre d'inertie du solide varie (accélération).
La deuxième loi de newton établit que la somme vectorielle des forces extérieures appliquées à un solide est égale au produit de la masse M du solide par l'accélération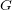 
de son centre d'inertie :
La direction et le sens de cette somme sont ceux de la variation du vecteur vitesse entre deux instants proches.
Troisième loi de newton : principe des actions réciproques
Cette loi stipule que l'action exercée sur un système produit toujours une réaction de la part de ce dernier.
Si un système A exerce une action mécanique sur un système B, modélisée par la force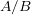 
, alors le système B exerce une action mécanique sur A, modélisée par la force 
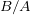, telle que :
| Loi | Nom | Énoncé Synthétique | Formule Clé |
|---|---|---|---|
| 1ère Loi | Principe d'Inertie | Un corps isolé ou pseudo-isolé est soit au repos, soit en mouvement rectiligne uniforme. |  |
| 2ème Loi | Relation Fondamentale de la Dynamique | La somme des forces appliquées à un corps est égale au produit de sa masse par l'accélération de son centre d'inertie. |  |
| 3ème Loi | Principe des Actions Réciproques | Si A exerce une force sur B, alors B exerce une force opposée et de même norme sur A. |  |
La force : action mécanique et modélisation vectorielle
Définition d'un système et des actions
Un système d'étude est constitué d'un ou plusieurs corps limités par des frontières précises et possédant une masse. La définition de ce système permet de considérer un milieu extérieur agissant sur lui.
Les actions mécaniques exercées sur le système se traduisent par deux effets principaux : la déformation du système et la modification de son mouvement (trajectoire, vitesse).
Actions de contact et à distance
Les actions de contact nécessitent un contact entre l'acteur et le receveur. Elles sont réparties en surface (surfacique) ou ponctuelles.
Les actions à distance n'exigent pas de contact. On en connaît deux principales : l'interaction électromagnétique et l'interaction gravitationnelle. Elles sont réparties en volume (volumique).
Le vecteur force et ses caractéristiques
Le vecteur force est une modélisation d'une action mécanique sur un système. Il possède les caractéristiques suivantes :
- Direction et sens : ceux de l'action mécanique.
- Valeur : exprimée en newton (N), liée à l'intensité de l'action.
- Point d'application : modélisation de la surface ou du volume concerné. Pour les actions à distance, il est souvent placé au centre d'inertie (centre de répartition des masses).
Forces usuelles
- Le poids (
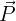) : action exercée par la terre. Verticale vers le bas. Point d'application : centre d'inertie. Valeur : 
. - La poussée d'archimède (
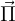) : action exercée par un fluide. Verticale vers le haut. Point d'application : centre de gravité du volume de fluide déplacé. Valeur : 
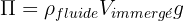. - La réaction des supports (
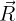) : perpendiculaire au support. - Les forces de frottements (
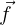) : parallèle au support, s'opposent au mouvement.
Équilibre et énergies du mouvement
Condition d'équilibre
L'équilibre d'un système se définit comme l'immobilité dans un référentiel donné. Pour qu'il y ait équilibre, il faut que la somme vectorielle des forces appliquées au système soit nulle, ce qui correspond à la condition des systèmes pseudo-isolés.
L'énergie cinétique
L'énergie cinétique est l'énergie d'un objet en mouvement. Elle dépend de la vitesse du corps et du référentiel d'étude. Elle est donnée par la formule (pour un corps en translation) :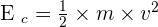
- Ec : énergie cinétique en joule (J).
- m : masse de l'objet en kilogramme (kg).
- v : vitesse de l'objet en mètre par seconde (m/s).
L'énergie potentielle
L'énergie potentielle dépend de la position relative des différentes parties du système, souvent liée à la hauteur au-dessus du sol (énergie potentielle de pesanteur). Elle est donnée par la formule :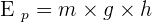
- Ep : énergie potentielle en joule (J).
- g : intensité de pesanteur (approx.
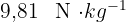). - h : hauteur.
L'énergie mécanique
L'énergie mécanique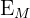 
d'un système est la somme de son énergie cinétique 
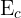et de son énergie potentielle 
:
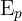L'énergie mécanique dépend également du référentiel d'étude.
Le champ gravitationnel et la gravité
La gravitation correspond à une force attractive qui s'exerce à distance entre deux corps qui ont une masse. Cette force dépend :
- De la distance : plus elle est grande, plus la force est petite.
- De la masse des corps : plus elle est grande, plus la force gravitationnelle est grande.
Le champ gravitationnel est un champ réparti dans l'espace dû à la présence d'une masse qui exerce une influence gravitationnelle sur les corps à proximité. L'introduction du champ permet de s'affranchir du problème de la médiation de l'action à distance.
L'approximation newtonienne est valable pour des corps présentant une vitesse faible par rapport à celle de la lumière et si le potentiel gravitationnel est faible.
Vous avez aimé cet article ? Notez-le !
Loading...
Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !
enonce de la premiere loi de Newton : il faut tout le temps preciser sila somme vectorielle des forces appliquees à ce systeme est NULLE precise tout le temps somme