Chapitres

La conduction
Tous les métaux sont conducteur. Un métal est constitué d'atomes. Dans les atomes, certains électrons sont peu liés au noyau : ce sont les électrons libres. Le générateur provoque leur mise en circulation. Dans un métal, le courant électrique est dû à une circulation ordonnée d'électrons libres. Les électrons libres, négatifs se dirigent vers la borne plus du générateur et sont refoulés par la borne négative. Le sens de circulation des électrons est opposé au sens conventionnel du courant.
Le courant électrique
Le courant continu, noté CC en Français ou DC en Anglais, correspond à un courant électrique dont l'intensité reste indépendant du temps, on dit donc de celle-ci qu'elle est constante. C'est notamment le type de courant qui est délivré par les piles ou encore les accumulateurs. On peut donc appeler courant continu tout courant périodique dont l'intensité reste toujours relativement proche de sa valeur moyenne ou encore un courant périodique dont la composante continue c'est-à-dire sa valeur moyenne est d'importance primordiale. Il est également possible de nommer courant continu tout courant électrique qui circule de façon continue ou très majoritairement dans le même sens. On dit alors de ce courant qui est unidirectionnel.

Le courant électrique dans les solutions
Nous avons vu que le courant dans les métaux est dû aux électrons libres qui se déplacent sous l'impulsion d'une tension électrique. D'un mouvement désordonné, ils passent à un mouvement ordonné.
Dans les solutions, il n'y a pas d'électrons, la conduction est assurée par d'autres porteurs de charges : les ions. Lorsqu'on branche un générateur à une cellule électrolytique, les ions contenus dans la cellule vont circuler dans les deux sens puisque contrairement aux métaux, les charges positives se déplacent. Le courant électrique est assuré par la double migration des ions.
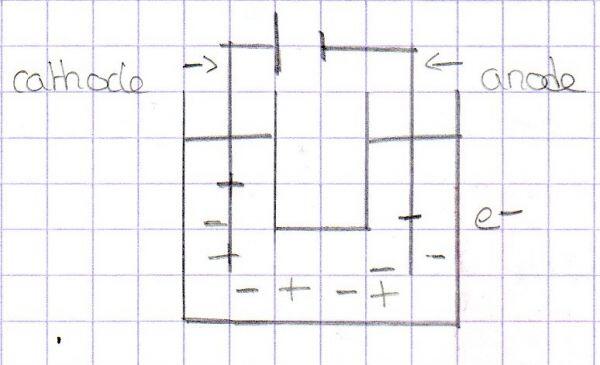
Conductance d'une solution ionique
Définition de la conductance
En électricité, on définit la conductance comme étant la capacité d'un corps à laisser passer une certaine quantité de courant électrique lorsqu'il est soumis à une différence de potentiel.
On se rappelle que la résistance électrique notée R est mesurée en ohm Ω. Elle traduit la capacité d'un conducteur à 'résister' au passage du courant. Cette notion se traduit par la loi d'ohm.
u = R . I
Pour les solutions électrolytiques, il en est de même que pour les conducteurs, elles résistent au courant. Par commodité, les chimistes préfèrent utiliser la conductance de la solution qui est l'inverse de sa résistance.
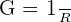
On la note G (siemens S). La conductance traduit la capacité d'une solution à conduire le courant.
Loi d'ohm d'une solution électrolytique : I = G . U

Mesure de la conductance
On appelle cellule conductimétrique, l'ensemble constitué des deux électrodes et de la solution. Pour mesurer la conductance d'une cellule, on mesure I et U, on fait le rapport
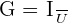
Facteur qui influence G
Paramètres géométriques
Il y a deux paramètres géométriques qui modifient la conductance :
L'écartement entre les électrodes : L
Plus L est grande, moins les ions sont capables de faire la distance entre les électrodes. Ils sont freinés par les entités chimiques présentes en solution.
La surface immergée des électrodes : S
Plus S est grande, plus il y a d'ions susceptibles de passer d'une électrode à l'autre.
Après les études quantitatives, on en déduit la formule :
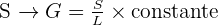
Avec :
- S en m² ;
- L en m.
Conductivité d'une solution
Les chimistes ont construit les électrodes conductimétriques standard pour s'affranchir des paramètres géométriques S et L. La seule mesure restante est la constante que l'on nomme conductivité de la solution et qui est caractéristique de cette solution. On la note σ et se mesure en S/m.

Facteurs qui influencent σ
La grandeur σ ne dépend que de la solution, elle varie selon trois paramètres :
- La concentration : plus la solution est concentrée, plus la quantité d'ions permettant la conduction est grande, donc σ augmente.
- La nature des ions en solution : selon leur taille, leur charge, et la solvatation qu'ils subissent les ions circulent plus ou moins bien en solution, ils influencent donc la valeur de σ.
- La température : cette grandeur est liée à l'agitation des molécules et plus celle-ci est grande, plus elle favorise la conduction.
Voici un tableau qui relie les paramètres géométriques et la conductance :
| Paramètre | Symbole | Effet sur G |
|---|---|---|
| Écartement entre électrodes | L | Plus L est grand → G diminue |
| Surface immergée des électrodes | S | Plus S est grande → G augmente |
Ainsi qu'un tableau qui répertorie les facteurs influençant la conductivité σ :
| Facteur | Effet sur σ |
|---|---|
| Concentration | Plus la concentration est élevée → σ augmente |
| Nature des ions | Selon taille, charge et solvatation → influence σ |
| Température | Plus la température est élevée → σ augmente |
Conductivité molaire
Définition
La conductivité molaire d'une solution est le rapport entre la conductivité et la concentration des ions qu'elle contient.
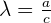
Λ ne dépend pas de la concentration mais seulement de la température et de la nature des ions. On peut établir pour chaque ion, une conductivité molaire ionique λ.
Et dans le cas général, si le soluté s'écrit M+(aq) + X-(aq) on aura les deux conductivités molaires λM+ + λX- dont la somme est égale à la conductivité molaire de la solution.
λM+ + λX- = Λ
Les tables de conductivités
Les conductivités molaires des ions sont mesurées à plusieurs reprises à diverses concentrations en gardant les autres paramètres fixes. De cette manière, les chimistes ont obtenu les conductivités molaires ioniques des ions pour des dilutions infinies (concentration nulle). Elles sont notées λ0.
Ces conductivités molaires ioniques sont reportées dans les tables répertoriées.
Remarque : Elles ne sont valables que pour des concentrations inférieures à 10-2 mol/L.
| Ion | Conductivité molaire λ₀ (S·m²/mol) |
|---|---|
| Na⁺ | 50.1 × 10⁻⁴ |
| Cl⁻ | 76.3 × 10⁻⁴ |
| K⁺ | 73.5 × 10⁻⁴ |
| OH⁻ | 198 × 10⁻⁴ |
Exercices
Voyons maintenant 3 exercices pour s'entraîner sur le sujet :
On se propose d’identifier deux espèces chimiques acides différentes notées HA1 et HA2, en utilisant quelques mesures expérimentales.
Tout d’abord, on prépare deux solutions aqueuses S1 et S2, à partir des espèces HA1 et HA2 et d’eau distillée, de telle manière que la concentration en soluté apporté soit c0 = 1,0 x 10-2 mol.L–1 pour chacune d’elles. On considère que la réaction de chaque espèce acide dans l’eau est instantanée.
1. Mesure par pH-métrie :
1.1. Définir une espèce acide selon Brönsted.
1.2. Écrire l’équation qui représente la réaction d’une espèce acide quelconque HA avec l’eau. Indiquer les deux couples acide/base mis en jeu.
1.3. Quelle relation a-t-on, dans ces conditions, entre les quantités de matière de A– et H3O+ ?
1.4. Mesure du pH à 25°C sur V = 200 mL de chaque solution :
[H3O+]1 = 1,3 x 10–3 mol.L-1 pour S1 et [H3O+]2 = 1,0 x 10–2 mol.L-1 pour S2.
1.4.1. Calculer les quantités de matière en ions oxonium n(H3O+)1 et n(H3O+)2 dans chaque solution.
1.4.2. Calculer la quantité de matière d’acide HA1 et HA2, initialement présente dans les 200 mL de chaque solution.
1.4.3. Exprimer l’avancement maximal de la réaction et calculer sa valeur. Calculer l’avancement final xf1 et xf2 pour chaque acide.
1.5. Préciser la signification du taux d’avancement final et calculer t1 et t2.
2. Suivi spectrophotométrique :
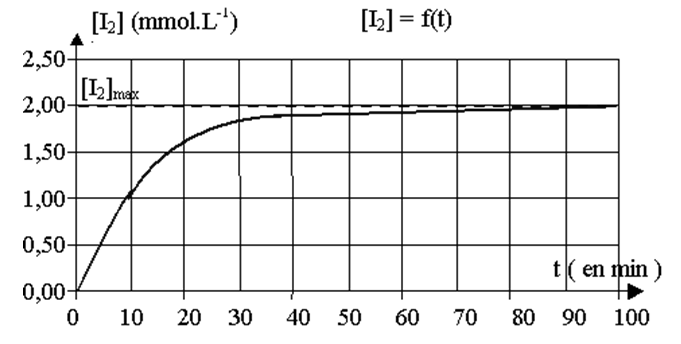
Pour identifier précisément l’espèce acide qui participe à la réaction, on introduit dans les 200 mL de cette solution 4 mL d’une solution de peroxyde d’hydrogène H2O2 (c = 0,10 mol.L-1). On observe l’apparition d’une coloration jaune caractéristique du diiode en solution aqueuse.
Réaction (1) : H2O2 (aq) + 2 H3O+ (aq) + 2 I– (aq) → 4 H2O (l) + I2 (aq)
2.1. Par spectrophotométrie, tracer l’évolution de la concentration en diiode formé au cours du temps. Déterminer la vitesse de réaction et le temps de demi-réaction.
2.2. Identifier les couples oxydant/réducteur et la substance qui subit l’oxydation. Identifier l’espèce acide HA.
3. Mesure conductimétrique :
On mesure la conductivité de la solution de l’autre acide (sexp = 53,4 mS.m-1). Exprimer la conductivité molaire ionique de la base conjuguée et identifier la nature de l’acide.
| Formule de l’ion | H3O+ | NO3– | HCOO– | HO– | CN– |
|---|---|---|---|---|---|
| λ (mS.m².mol-1 ) | 35,0 | 7,14 | 5,46 | 19,9 | 7,80 |
1.1. Définition : Selon Brönsted, un acide est une espèce capable de céder un proton (H+) à une autre espèce.
1.2. Réaction générale d’un acide HA avec l’eau :
HA + H2O → H3O+ + A–
Couples acide/base : HA / A– et H2O / H3O+
1.3. Relation entre les quantités : n(H3O+) = n(A–) = xf (avancement final de la réaction)
1.4. Quantités de matière :
n(H3O+) = [H3O+] × V
n(H3O+)1 = 1,3 × 10-3 × 0,2 = 2,6 × 10-4 mol
n(H3O+)2 = 1,0 × 10-2 × 0,2 = 2,0 × 10-3 mol
Quantités initiales d’acide : n(HA) = c × V = 1,0 × 10-2 × 0,2 = 2,0 × 10-3 mol
Avancement final :
xf1 = 2,6 × 10-4 mol
xf2 = 2,0 × 10-3 mol
Taux d’avancement : t = xf/n0
2. Réaction d’oxydoréduction : H2O2 + 2 H3O+ + 2 I– → 4 H2O + I2
Couples oxydant/réducteur : I2/I– et H2O2/H2O
Oxydation : I– → I2
3. Conductimétrie :
σ = λ(H3O+) × [H3O+] + λ(A–) × [A–]
λ(A–) = (σ - λ(H3O+) × [H3O+]) / [A–]
Préparation de la solution Adiaril® pour réhydratation et titrage des ions chlorure.
1. Écrire l’équation de la réaction avec AgNO3 et calculer le quotient de réaction initial Qr,i. Commenter le sens d’évolution.
2. Préparation de la solution pour titrage :
2.1. Verrerie à utiliser pour préparer 200 mL de solution et prélever 20 mL.
2.2. Calculer la conductivité avant et après l’équivalence et identifier les ions responsables.
3. Exploitation :
3.1. Déterminer sur le graphe le volume de nitrate d’argent versé à l’équivalence.
3.2. Déduire la concentration des ions chlorure.
3.3. Calculer la masse mexp d’ions chlorure dans le sachet et l’erreur relative.
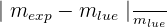

Réaction support : Ag+ + Cl– → AgCl(s)
Quotient de réaction : Qr = [AgCl] / ([Ag+][Cl–])
Qr,i ≪ K, donc réaction totale vers la formation du précipité AgCl
Avant équivalence : ions principaux : Na+, Cl–, Ag+
Après équivalence : excès Ag+, Na+
Volume à l’équivalence : lecture graphique Veq
Concentration Cl– : CCl = n/Veq
Masse mexp = CCl × M(Cl) × V(sachet)
Erreur relative = |mexp - mlue| / mlue
Les dépôts de tartre (CaCO3) peuvent être dissous par des solutions acides comme les détartrants commerciaux.
Données : Masse volumique de la solution de détartrant, masse volumique du carbonate de calcium, masses molaires, surface d’un cylindre.
1. Détermination de la concentration en acide chlorhydrique :
1.1. Montrer que la concentration molaire est de l’ordre de 2,6 mol.L-1.
1.2. Identifier les couples acido-basiques dans le titrage par NaOH.
1.3. Montrer que le volume nécessaire dépasse la burette graduée de 25 mL.
1.4. Déterminer la concentration molaire dans la solution diluée et vérifier la compatibilité avec l’étiquette.
2. Utilisation domestique :
Équation de réaction sur le tartre : 2 H3O+ + CaCO3 → Ca2+ + CO2 + 3 H2O
2.1. Estimer le volume total de tartre sur la surface extérieure du tambour du lave-linge.
2.2. Vérifier si le flacon de 750 mL de détartrant commercial est suffisant.

1. Concentration en HCl :
9 g pour 100 g → c = (9 g / 36,5 g/mol) / (100 g / 1,04 × 103 g/L) ≈ 2,6 mol/L
Couples acido-basiques pour le titrage : H3O+/H2O et HO–/H2O
2. Réaction sur le tartre : 2 H3O+ + CaCO3 → Ca2+ + CO2 + 3 H2O
Volume de tartre : V = surface × épaisseur ≈ (2πR2 + 2πRh) × 10 × 10-6 m
Quantité de H3O+ nécessaire : n = 2 × n(CaCO3)
VHCl = n / c(H3O+)
Comparaison avec flacon 750 mL → suffisant ou non.
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !