Chapitres
- 01. Objectif
- 02. Composition
- 03. Données sur les espèces chimiques mises en jeu
- 04. Principe du dosage
- 05. Exploitation

Objectif
Déterminer
le pourcentage massique en fer d'une solution commerciale
d'anti-mousse et confronter les résultats avec les données de
l'étiquette :
CompositionTeneur soit |
Données sur les espèces chimiques mises en jeu
| Masse Les Les |
Principe du dosage
La
solution commerciale So étant trop concentrée, on la dilue 3 fois :
la solution diluée obtenue est S1. On prélève un volume : V1 =
10,0 mL de la solution S1, que l'on verse dans un bécher sec et
propre. On réalise alors un dosage colorimétrique de l'échantillon
prélevé.
L'équivalence
du dosage est obtenue lorsqu'on a versé : Vequiv = 16,1
mL d'une solution de permanganate de potassium ( contenant les ions
permanganates MnO4- ( aq ) ), de concentration
molaire volumique en soluté apporté C = 5,00 . 10-2
mol.L-1.
Exploitation
1
: Donner le protocole de préparation de 150 mL de solution diluée
S1 à partir de la solution commerciale S0.
Protocole
pour préparer la solution S1 par dilution de S0 :
V1
= 150 mL, et C1 = C0 / 3 ; il faut donc prélever un volume V0 de la
solution commerciale tel que V0 = V1 / 3 soit V0 = 150 / 3 = 50 mL.
2
: Faire un schéma du dispositif de dosage en précisant les espèces
titrante et titrée.
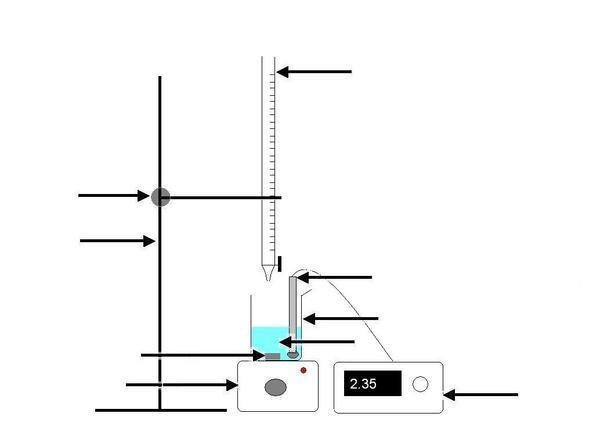
L'espèce
titrée ( dans le bécher ou erlenmeyer ) : ion fer II ; Fe2+.
L'espèce
titrante ( dans la burette ) ; ion permanganate MnO4-
3
: Donner les demi-équations des deux couples mis en jeu.
Fe2+
= Fe3+ + e-
MnO4-
+ 8H+ + 5e- = Mn2+ + 4H2O
4
: S'agit-il de couples oxydant / réducteur ou acide / base ?
Justifier.
Il
s'agit d'une réaction d'oxydo-réduction car il y a un échange
d'électrons.
5
: Écrire l'équation chimique de la réaction support du dosage.
MnO4-
+ 8H+ + 5Fe2+ → 5Fe3+ + Mn2+
+ 4H2O
6
: Définir l'équivalence d'un dosage. Comment le repérer ici ?
L'équivalence
est atteinte quand les deux réactifs ( MnO4-
et Fe2+ ) sont dans les proportions stœchiométriques ;
ici cela se traduit par le passage de l'incolore ( jaune ) au violet.
7
: Dresser le tableau d'avancement de la réaction à l'équivalence.
| MnO4- | ||||||
| Initial | neq | Excès | n1 | 0 | 0 | Excès |
| Final ( | neq | Excès | n1 = | 5 | Xeq | Excès |
8
: En déduire une relation entre la quantité de matière n1 d'ion
fer ( Fe2+ ) contenu dans l'échantillon dosé et la
quantité de matière neq d'ion permanganate ( MnO4-
) versée à l'équivalence.
On
a neq – Xeq = 0 = N1 – 5 Xeq.
Donc
Xeq = neq = N1 / 5 soit N1 = 5 * neq.
9
: En déduire la concentration C1 de la solution S1.
N1
= C1 * V1 et neq = C * Veq
Donc
C1 * V1 = 5 * C * Veq
C1
= ( 5 * C * Veq ) / V1
C1
= ( 5 * 5.10-2 * 16,1 ) / 10
C1
= 4,03.10-1 mol.L-1
10
: Calculer la concentration C0 de la solution commerciale S0.
La
solution commerciale est 3 fois plus concentrée que S1 donc S0 = 3 *
C1
C0
= 4,03.10-1 * 3 = 1,21 mol.L-1
11
: En déduire le titre massique en ions fer de S0, est-ce en accord
avec l'étiquette.
Le
titre massique en fer est t :
t
= C0 * M
t
= 1,21 * 55,8
t
= 67,4 g.L-1
ce
qui est en accord avec l'étiquette ( 67,5 g.L-1 )
12
: La densité de S0 est d = 1,13. Quelle est la masse d'un litre de
solution commerciale S0 ?
D
= 1,13 donc la masse d'un litre de solution est 1,13 kg soit 1130 g.
13
: En déduire le pourcentage en masse de fer. Comparer avec la donnée
de l'étiquette.
Le
pourcentage en fer est 67,4 * 100 / 1130 = 5,96 % soit presque 6% !
Résumer avec l'IA :























Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !