Terminale – Les suites : Limites de Suites

Voici un cours pratique sur les suites réalisé par des ambassadeurs Superprof qui ont lancé leur application de e-learning, Studeo : preview exclusive pour Superprof !

Il se décompose en deux temps :

• une vidéo de cours de 5 minutes pour comprendre les points clés,
• un exercice d'application et sa vidéo de correction pour maîtriser la méthode.

Les meilleurs professeurs disponibles

4,9 (105 avis)

Salomé

20€

/h

1^er cours offert !

4,6 (117 avis)

Laurent

60€

/h

1^er cours offert !

5 (96 avis)

Adlane

50€

/h

1^er cours offert !

5 (54 avis)

Davina

17€

/h

1^er cours offert !

4,9 (105 avis)

Salomé

20€

/h

1^er cours offert !

4,6 (117 avis)

Laurent

60€

/h

1^er cours offert !

5 (96 avis)

Adlane

50€

/h

1^er cours offert !

5 (54 avis)

Davina

17€

/h

1^er cours offert !

C'est parti

1) Limite finie - le cours en Terminale

Vidéo Antonin - Cours :

https://youtu.be/bfFTdM3H4uk

À retenir sur ce point de cours :

section{Définitions de limites}

- Convergence vers un réel : Idée de couloir aussi petit qu'on veut - I Ça ne vient pas toujours se coller de manière propre !

On dit que la suite 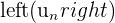tend vers un réel 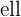quand tend vers , si tout intervalle ouvert contenant 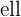contient tous les termes de la suite à partir d'un certain rang.

On dit que 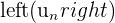converge et on note .

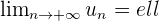- Divergence en et

On dit que la suite 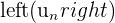tend vers quand tend vers , si pour tout réel 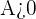, l'intervalle ] 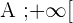contient tous les termes de la suite à partir d'un certain rang.

On dit que 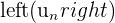diverge et on note .

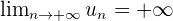On dit que la suite 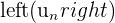tend vers quand tend vers , si pour tout réel 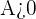, I'intervalle ] 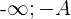[ contient tous les termes de la suite à partir d'un certain rang.

On dit que 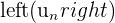diverge et on note .

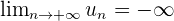- Points supplémentaires:

- Unicité de la limite

- On peut être divergent sans partir vers ou -\infty

2) Limite avec A ou Ɛ - exercice d'application

Avant de voir la vidéo de correction ci-dessous, vous pouvez vous essayer à l'exercice d'application suivant :

Démontrer une limite avec ou epsilon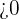

Soit 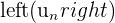la suite définie par .

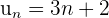a) Pour tout réel 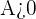, déterminer le plus petit entier naturel 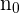tel que pour tout entier .

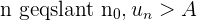b) En déduire la limite de la suite .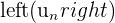

Property of Studeo LLC

Vidéo Kevin - Application :

https://youtu.be/h9xy0BjNylc

Vous pouvez également retrouver le pdf du superprof ici :

PDF Les suites : Limites de suite

Pour retrouver ces vidéos, ainsi que de nombreuses autres ressources écrites de qualité, vous pouvez télécharger l'application Studeo (ici leur website) pour iOS par ici ou Android par là !