Entraînement de Maths : les Nombres Complexes
Exercices sur les expressions à chiffre imaginaire Exercice 1 Ecrire sous forme trigonométrique les complexes suivants : a) b) c) d) e) Exercice 2 Le cercle de Nyquist (utilisé en électronique) Les nombres a, b, c et d sont des réels donnés ; x est un réel variable. Soit le complexe : et M son image dans le[…]
18 juin 2007 ∙ 1 minute de lecture
Devoir de Mathématiques : la Proportionnalité
Contrôle sur les proportions en maths Exercice 1 Complétez les tableaux suivants sachant que ce sont des tableaux de proportionnalité : 5 15 8 ............ 4 3 9 ........ 9 ....... 6 7 Exercice 2 Soit V la distance d' un trajet . Soit[…]
3 juin 2007 ∙ 1 minute de lecture
Sujet et Corrigé du Brevet de Maths de 2005
Les questions de l'épreuve de mathématiques LIEN VERS DE NOMBREUX DOCUMENTS POUR BIEN PREPARER ET REUSSIR LE DIPLOME NATIONAL DU BREVET EN JUIN ECHEC ET MATHS
15 avril 2007 ∙ 1 minute de lecture
La Détermination de la Médiane en Maths
Établir la valeur médiane grâce aux données Les notes du dernier contrôle de mathématique sont consignées dans le tableau suivant : Notes 5 7 9 10 11 12 13 14 15 16 20 Effectifs 1 5 7 4 3 4 5 3 3 1 1 Compléter le tableau suivant : Notes 5 7 9 10 11 12[…]
7 avril 2007 ∙ 1 minute de lecture
La Raisonnement par l’Absurde
Faire une démonstration logique par l'apagogie Définition Le raisonnement par l'absurde (du latin reductio ad absurdum) ou apagogie (du grec ancien apagôgê ) est une forme de raisonnement logique, philosophique, scientifique consistant soit à démontrer la vérité d'une proposition en prouvant l'absurdité de la proposition contraire, soit à montrer la fausseté d'une autre proposition en[…]
2 février 2007 ∙ 1 minute de lecture
La Méthode du Contre-Exemple
Prouver qu'une affirmation est fausse Définition Un contre exemple est un exception à une règle générale : dans un cas particulier, cette règle est fausse. Un contre exemple permet donc de prouver qu'une affirmation est fausse. Trouver un contre exemple pour prouver qu'une proposition est fausse peut être parfois aussi difficile que trouver la démonstration[…]
2 février 2007 ∙ 1 minute de lecture
Corrigé du Brevet des Collèges de Maths en 2006
Questions numériques, géométriques et problème J'ai trouvé le sujet du brevet sur un autre (merci). Comme il n'est pas corrigé, je vais rédiger un corrigé en 3 documents, un par partie (Partie numérique, partie géométrie et Problème). ESSAYER DE FAIRE VOUS MEME AVANT DE VOIR LE CORRIGE les autres parties .... plus tard. BON COURAGE[…]
23 décembre 2006 ∙ 1 minute de lecture
Solution : les Énigmes Mathématiques
Corrigé des exercices ludiques de maths 1- Les âges (1) Désignons mon âge par x et le vôtre par y : notre différence d'âge est donc de ( x-y ) années. "J’ai deux fois l’âge que vous aviez quand j’avais l’âge que vous avez", se traduit par : quand j'avais l'âge y, vous aviez y-(x-y)[…]
23 décembre 2006 ∙ 3 minutes de lecture
Corrigé du Brevet des Collèges de Mathématiques en 2006
Solution de l'épreuve de maths Exercice 1 1. Calculer A en détaillant les étapes du calcul. Donner le résultat sous forme d'une fraction irréductible. A = 1/3 + 5/6 : 3/2 = 1/3 + (5 / 6) x (2 / 3) = 1/3 + (5 x 2) / (2 x 3 x 3) ([…]
23 décembre 2006 ∙ 4 minutes de lecture
Exercice Type Brevet : les Équations
Développer, réduire et factoriser Exercice Soit D = ( x - 3)2 + ( x - 3 ) ( 9x - 4 ). 1) Développer et réduire D. 2) Factoriser D. 3) Calculer D pour x = 2 4) Résoudre l'équation ( x - 3) ( 10x - 7) = 0. Correction 1) Développer et[…]
29 novembre 2006 ∙ 2 minutes de lecture
Pythagore
Qui était-il ? Présentation Ce programme permet d'appliquer le théorème de Pythagore. Il fournit toutes les informations nécessaires permettant de donner un résultat exact et un résultat approché (si racine carrée non exacte) Tout comme le premier document, les numéros répertorient les lignes. Programme ClrText "************** PYTHAGORE **************"[entré en bas] ClrText "VOICI LA" "FORMULE" "UTILISEE:"[…]
3 octobre 2006 ∙ 1 minute de lecture
Tracer une Courbe
Comment réussir en géométrie ? Un graphique, par exemple une courbe de résultats, permet de visualiser les variations d'une grandeur mesurée (y) en fonction d'une autre grandeur (x) qui varie naturellement (le temps, la distance, ... ) ou que l'on fait varier au cours d'une expérience. Pour cela je dois : Déterminer les données à représenter[…]
27 septembre 2006 ∙ 2 minutes de lecture
Valeur Actuelle en Intérêts Composés
Comment effectuer ce calcul ? Définition La valeur actuelle d'un capital Cn est égale à : C0 = Cn / ( 1 + i ) n = Cn ( 1 + i ) -n n est le nombre d'années de placement i est le taux d'intérêt (composé) Exemples
26 septembre 2006 ∙ 1 minute de lecture
La Valeur Actuelle
Comment calculer les intérêts simples ? La valeur actuelle d'un capital (intérêt simple) La valeur actuelle C0 d'un capital Ct obtenu à l'instant t est la somme qu'il faut placer à t = 0 pour récupérer Ct. La valeur actuelle peut s'interpréter aussi comme le montant équivalent à t = 0 d'un capital Ct disponible[…]
25 septembre 2006 ∙ 1 minute de lecture
Le Zéro-Coupon et Les Intérêts Simples
Qui rémunère le prêteur ? Définition Une opération zéro-coupon est une opération élémentaire à deux flux F0 et F1 , l'un reçu, l'autre payé. Par exemple, c'est le cas l'achat d'une obligation suivie de sa revente, du décaissement d'un prêt suivi de son remboursement .. L'intérêt i est la différence entre le flux final à[…]
21 septembre 2006 ∙ 2 minutes de lecture
Equations à Une Inconnue
Comment les résoudre ? Quelques exercices Equation 1 : 4 ( 3 x + 12) + 4 (4 x - 8) = 5 x - 7 Equation 2 : 8 ( 1 - 3 x) = 6 ( 3 x + 9) Equation 3 : 5 x + 7 = 3 x + 6 Pour[…]
16 septembre 2006 ∙ 1 minute de lecture
Figures Géométriques
Comment utiliser GEONExT ? Présentation Pour faire une figure géométrique, c'est très simple. Il te suffit de télécharger gratuitement le logiciel GEONExT en cliquant sur le lien suivant : http://geonext.uni-bayreuth.de/content/int/download/index.html?CD=CD Explications Une fois que tu as installer GEONExT, tu peux télécharger un tutorial à l'adresse suivante afin de te familiariser avec les commandes : http://www.framasoft.net/IMG/GEONExT.pdf. Pour[…]
22 août 2006 ∙ 2 minutes de lecture
Le Faucon et le Chapon
Fable de la Fontaine Le Faucon et le Chapon Une traîtresse voix bien souvent vous appelle; Ne vous pressez donc nullement : Ce n'était pas un sot, non, non, et croyez-m'en, Que le chien de Jean de Nivelle. Un citoyen du Mans, chapon de son métier, Etait sommé de comparaître Par devant les lares du[…]
15 juillet 2006 ∙ 2 minutes de lecture
La Mouche et les Deux Marcheurs
Résolution de problème ENONCE Un marcheur M1 part de A vers B à t1 à la vitesse v1 = 4 km/h. Un marcheur M2 part de A vers B à t2 = t1 + 30 mn à la vitesse v2 = 6 km/h. Une mouche part de A vers B à t2 à la vitesse[…]
24 juin 2006 ∙ 2 minutes de lecture
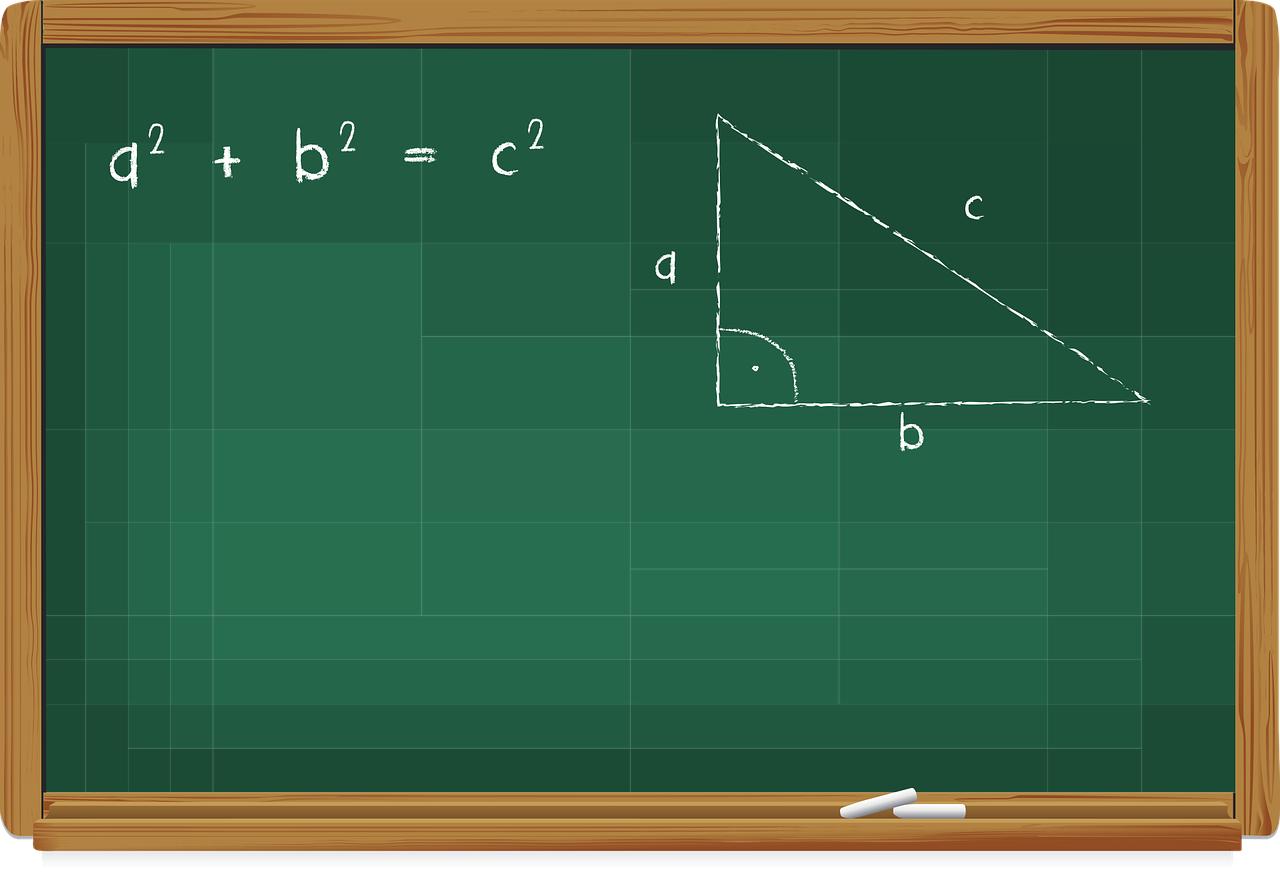
L’Hypoténuse
Le triangle rectangle L'hypoténuse Dans un triangle rectangle, l'hypoténuse est le côté de la plus grande longueur. Exemple : Le triangle ABC est restangle en A : le côté [BC] est l'hypoténuse.
21 juin 2006 ∙ 1 minute de lecture
Définition d’une Équation
Terminologie mathématique Une équation est une égalité comprenant une ou plusieurs lettres. Cette lettre est appelée inconnue. Résoudre une équation c'est déterminer la ou les valeurs de l'inconnuepour laquelle ou lesquelles elle est vraie. Cette ou ces valeurs s'appellent la ou les solutions de l'équation. exemple: 2x + 6 = 23 2x = 23 - 6 2x = 17 x = 17 : 2[…]
4 avril 2006 ∙ 1 minute de lecture