Qu'est-ce que le marnage ?

Par Clément

Rédigé le 12 juillet 2022

2 minutes de lecture

Chapitres

01. Questions
02. Réponses

Les meilleurs professeurs de Maths disponibles

Questions

Le marnage désigne la différence de hauteur entre la basse mer et la pleine mer qui suit.

On considère qu’à partir du moment où la mer est basse, celle-ci monte de 1/12 du marnage pendant la première heure, de 2/12 pendant la deuxième heure, de 3/12 pendant la troisième heure, de 3/12 pendant la quatrième heure, de 2/12 pendant la cinquième heure et de 1/12 pendant la sixième heure. Au cours de chacune de ces heures, la montée de la mer est supposée régulière.

1) À quel moment la montée de la mer atteint-elle le quart du marnage ?

2) À quel moment la montée de la mer atteint-elle le tiers du marnage ?

Réponses

1) Ici on remarque qu’au bout de 2 heures nous sommes à :

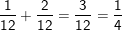
\dpi{100} \fn_cm \small \frac{1}{12}+\frac{2}{12}=\frac{3}{12}=\frac{1}{4}

Donc le quart du marnage est atteint au bout de 2 heures.

2) $\dpi{100} \fn_cm \small \frac{1}{3}=\frac{4}{12}$

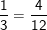
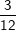
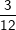
Nous sommes donc à $\dpi{100} \fn_cm \small \frac{3}{12}$ au bout de 2 heures, nous savons qu’elle va encore monter de $\dpi{100} \fn_cm \small \frac{3}{12}$ durant la prochaine heure.

Donc elle montera d’ $\dpi{100} \fn_cm \small \frac{1}{12}$ toutes les 20 minutes. Et pour arriver à $\dpi{100} \fn_cm \small \frac{4}{12}$ il faudra 2h20.

Vous avez aimé cet article ? Notez-le !

5,00 (3 note(s))

Clément

Freelancer et pilote, j'espère atteindre la sagesse en partageant le savoir que j'ai acquis lors de mes voyages au volant de ma berline. Curieux scientifique, ma soif de découverte n'a d'égale que la durée de demie-vie du bismuth 209.

Ces articles pourraient vous intéresser

La Divergence

Comment définit-on le laplacien en mathématiques ? Comme le rotationnel, le divergent ou encore le gradient, le laplacien est un opérateur mathématique qui permet de comprendre et d'étudier de nombreux domaines physiques comme l'électromagnétisme ou la mécanique des fluides. On le retrouve décliné en coordonnées cartésiennes, polaires (2D), cylindriques (3D), sphériques (3D), mais aussi à[…]

29 juillet 2024 ∙ 5 minutes de lecture

Statistiques : Révision Brevet

Ce qu'il faut savoir sur les statistiques en 3ème Les statistiques, une composante essentielle des mathématiques modernes, occupent une place de choix dans le programme du brevet des collèges. Elles permettent aux élèves de développer des compétences analytiques en interprétant des données et en tirant des conclusions éclairées. Cet article explore la notion de statistiques[…]

15 mai 2024 ∙ 2 minutes de lecture

Le PFS

Tout savoir sur le Principe Fondamental de la Statique, ou PFS 🌁 Le Principe Fondamental de la Statique (PFS) s'applique lorsque des solides parfaits et indéformables sont en équilibre. Il affirme que la somme des actions mécaniques extérieures est nulle, facilitant l'analyse en isolant des systèmes et en appliquant des méthodes de résolution graphiques ou[…]

30 janvier 2024 ∙ 6 minutes de lecture

Les fenêtres parallèles et perpendiculaires d'un immeuble

Démontrer que Deux Droites sont Parallèles ou Perpendiculaires

Que faut-il savoir au collège concernant les droites et leurs principales propriétés ? ? Pour démontrer que deux droites sont parallèles, vous pouvez vérifier que leurs pentes sont égales (même rapport), ou que les angles qu'elles forment avec une troisième droite sont égaux. ❌ Deux droites sont perpendiculaires si le produit de leurs pentes est[…]

7 novembre 2023 ∙ 5 minutes de lecture

Opérateur Laplacien – Définition

Comment définit-on l'opérateur laplacien en mathématiques ? L'opérateur laplacien est un opérateur différentiel de la dérivation partielle en mathématiques. Il est utilisé pour quantifier la variation et la courbure d'une fonction scalaire dans l'espace en mesurant la divergence du gradient de cette fonction. En d'autres termes, il permet d'analyser comment une quantité (comme une température,[…]

6 novembre 2023 ∙ 6 minutes de lecture

Le Programme de Mathématiques des Secondes

Quelles leçons allez-vous avoir à votre arrivée au lycée en classe de Seconde ? 🧮 Le programme de mathématiques en classe de seconde englobe divers domaines clés. Il commence par les ensembles de nombres, l'écriture et la comparaison des nombres, ainsi que les nombres premiers et les concepts d'algèbre comme le développement et la factorisation.[…]

31 août 2023 ∙ 9 minutes de lecture

jeune fille en train de résoudre un problème de maths

Les Formules Importantes pour le Brevet

L'essentiel à retenir avant l'examen du brevet en maths L'examen du brevet en deux mots 📚 L'examen du brevet en maths évalue les compétences essentielles acquises au collège. Les attentes portent sur : La compréhension et l'application de concepts géométriques (aires, périmètres, volumes) La résolution d'équations simples et la manipulation de fonctions La maîtrise des[…]

28 juillet 2023 ∙ 10 minutes de lecture

Arithmétique

Comment se préparer à l'épreuve de mathématiques du brevet ? Présentation de l'arithmétique L'arithmétique est une branche des mathématiques qui traite des nombres et des opérations arithmétiques telles que l'addition, la soustraction, la multiplication et la division. Elle est souvent considérée comme la base de toutes les mathématiques, car elle fournit les outils nécessaires pour[…]

11 mai 2023 ∙ 10 minutes de lecture

Les Différents Types de Capteurs

Comment automatiser une barrière de péage ? Les objectifs du TPE Dans le cadre des TPE, l'étudiant a un travail personnel à effectuer qui le met en situation de responsabilité. Cette activité constitue un entraînement à la démarche scientifique et/ou à la démarche technologique. Les TPE doivent faire appel à l'intelligence de situations concrètes car[…]

7 novembre 2022 ∙ 10 minutes de lecture

Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !

Laissez-nous un commentaire