Chapitres
Voici un cours pratique sur les suites réalisé par des ambassadeurs Superprof qui ont lancé leur application de e-learning, Studeo : preview exclusive pour Superprof !
Il se décompose en deux temps :
- une vidéo de cours de 5 minutes pour comprendre les points clés,
- un exercice d'application et sa vidéo de correction pour maîtriser la méthode.
1) Concept et Rédaction - le cours en Terminale
Vidéo Antonin - Cours :
https://www.youtube.com/watch?v=ooMM0OgD1pE&t=1s
À retenir sur ce point de cours :
Soit P(n) une propriété dépendant d'un entier naturel n
On suppose que:
(1) P(0) est vraie.
(2) Pour tout entier naturel n fixé, si P(n) est vraie, alors P(n+1) est vraie.
Alors pour tout entier naturel n, P(n) est vraie.
2) Récurrence et croissance - exercice d'application
Avant de voir la vidéo de correction ci-dessous, vous pouvez vous essayer à l'exercice d'application suivant :
Soit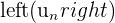 
la suite définie par 
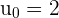et pour tout 
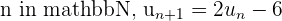. Montrer par récurrence que la suite 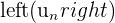est strictement décroissante.
Vidéo Kevin - Application :
https://www.youtube.com/watch?v=nfUy4UudJ9s
Vous pouvez également retrouver le pdf du superprof ici :
Pour retrouver ces vidéos, ainsi que de nombreuses autres ressources écrites de qualité, vous pouvez télécharger l'application Studeo (ici leur website) pour iOS par ici ou Android par là !
Résumer avec l'IA :
Vous avez aimé cet article ? Notez-le !
Loading...
Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !