Chapitres
- 01. Produit scalaire
- 02. Théorème d'Al Kashi
Produit scalaire
Le produit de deux vecteurs est un nombre. On dit que c'est le produit scalaire des deux vecteurs. Placons l'origine des deux vecteurs au même endroit.
Le produit scalaire des vecteurs et est égal à la longueur AB multipliée par la longueur AH. Il dépend donc de la norme (de la longueur) des deux vecteurs ainsi que de l'angle qu'il y a entre les deux. Si les deux vecteurs forment un angle droit alors le point H se retrouve en A et le produit scalaire est nul. On dit que 2 vecteurs sont orthogonaux si leur produit scalaire est nul. Si x est l'angle entre les deux vecteurs, alors :
D'une manière générale,
Si on connait les coordonnées des vecteurs et si et , alors .
Si et , donc les deux vecteurs ne sont pas othogonaux.
Théorème d'Al Kashi
Sache tout d'abord que l'on calcule avec un produit scalaire comme avec un produit normal et remarque que donc .
Donc du coup :
La relation suivante est le théorème d'Al-Kashi :
Si A est un angle droit, on retrouve le théorème de Pythagore.
Vous avez aimé cet article ? Notez-le !
Loading...
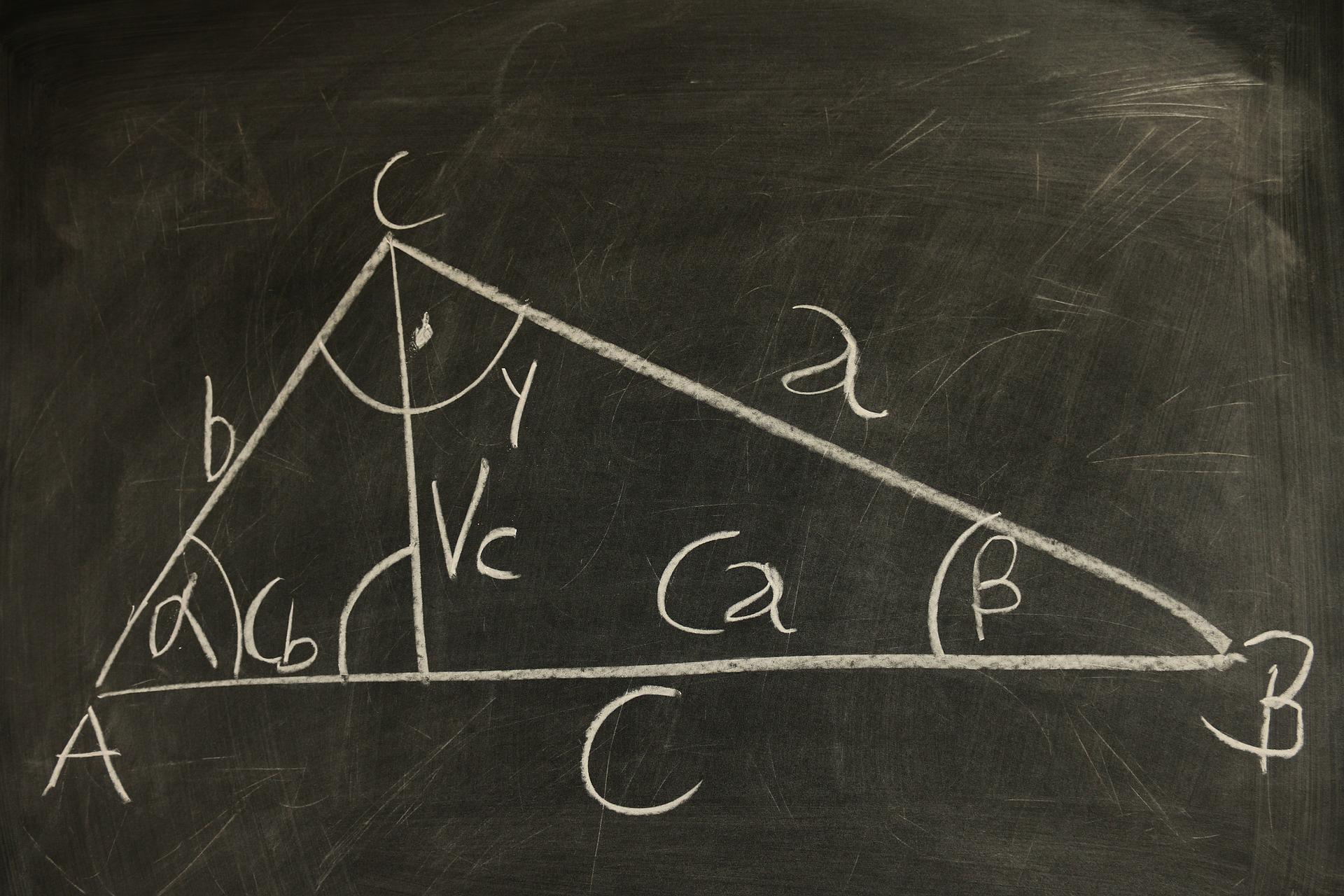
Si vous désirez une aide personnalisée, contactez dès maintenant l’un de nos professeurs !