Si vous touchez aux maths, vous ne devez être ni pressés, ni cupides, fussiez-vous roi ou reine.
Euclide (vers -300 avant J-C)
Comprendre les mathématiques n'est pas que calculer, résoudre ou développer un raisonnement logique, mais également en assimiler le lexique spécifique : c'est une langue à part entière.
Certes, les maths sont une matière scientifique mais on ne peut nier le caractère très littéraire de son vocabulaire.
en mathématiques selon l'enquête PISA de 2022, un chiffre en constant recul depuis 2000 (1).
Alors, pour progresser en cours de maths, voici donc un petit lexique, avec le vocabulaire essentiel des mathématiques2.
| Terme | Catégorie | Définition | Exemple |
|---|---|---|---|
| Algèbre | Algèbre et arithmétique | Branche des mathématiques utilisant des lettres pour représenter des quantités inconnues | Résoudre une équation avec une inconnue |
| Inconnue | Algèbre et arithmétique | Valeur à déterminer dans une équation | x + 3 = 5 |
| Équation | Algèbre et arithmétique | Égalité contenant une ou plusieurs inconnues | 2x + 5 = 13 |
| Facteur | Algèbre et arithmétique | Élément d'une multiplication | Dans 3 × 4, 3 et 4 sont des facteurs |
| Produit | Algèbre et arithmétique | Résultat d'une multiplication | Le produit de 3 × 4 est 12 |
| Somme | Algèbre et arithmétique | Résultat d'une addition | La somme de 5 + 3 est 8 |
| Terme | Algèbre et arithmétique | Élément d'une expression algébrique ou d'une suite | Dans 3x + 5, '3x' et '5' sont des termes |
| Différence | Algèbre et arithmétique | Résultat d'une soustraction | La différence de 10 - 4 est 6 |
| Dividende | Algèbre et arithmétique | Nombre à diviser dans une division | Dans 15 ÷ 3, 15 est le dividende |
| Quotient | Algèbre et arithmétique | Résultat d'une division | Le quotient de 15 ÷ 3 est 5 |
| Numérateur | Algèbre et arithmétique | Partie supérieure d'une fraction | Dans 3/4, 3 est le numérateur |
| Dénominateur | Algèbre et arithmétique | Partie inférieure d'une fraction | Dans 3/4, 4 est le dénominateur |
| Dénominateur commun | Algèbre et arithmétique | Dénominateur identique pour additionner ou comparer des fractions | Pour additionner 1/2 + 1/3, on utilise 6 comme dénominateur commun |
| Division euclidienne | Algèbre et arithmétique | Division avec quotient entier et reste | 17 ÷ 5 = 3 reste 2 |
| Fraction | Algèbre et arithmétique | Expression d'un rapport entre deux entiers | 3/4 représente trois quarts |
| Nombre | Algèbre et arithmétique | Concept mathématique représentant une quantité | Entiers, décimaux, naturels, relatifs |
| Nombres premiers | Algèbre et arithmétique | Nombres divisibles uniquement par 1 et eux-mêmes | 2, 3, 5, 7, 11, 13... |
| Nombre naturel | Algèbre et arithmétique | Nombres entiers positifs (notation ℕ) | 0, 1, 2, 3, 4... |
| Multiplicateur | Algèbre et arithmétique | Élément qui multiplie une quantité | Dans 5 × 3, 5 est le multiplicateur |
| PGCD | Algèbre et arithmétique | Plus grand diviseur commun à deux entiers | PGCD de 12 et 18 est 6 |
| Puissance | Algèbre et arithmétique | Nombre élevé à un exposant | 2⁴ = 2 × 2 × 2 × 2 = 16 |
| Racine carrée | Algèbre et arithmétique | Inverse du carré d'un nombre | √9 = 3 car 3² = 9 |
| Priorité des opérations | Algèbre et arithmétique | Ordre à respecter dans les calculs (PEMDAS) | Parenthèses, Exposants, Multiplication/Division, Addition/Soustraction |
| Diviseur | Algèbre et arithmétique | Nombre qui divise un autre sans reste | 3 est un diviseur de 12 |
| Carré magique | Algèbre et arithmétique | Carré de nombres où chaque ligne, colonne et diagonale a la même somme | Carré 3×3 avec somme magique 15 |
| Géométrie | Géométrie | Branche des maths qui étudie les formes et les espaces | Géométrie plane, géométrie dans l'espace |
| Triangle | Géométrie | Polygone à trois côtés | Triangle équilatéral, isocèle, rectangle, scalène |
| Carré | Géométrie | Figure à 4 côtés égaux et 4 angles droits | Cas particulier du rectangle |
| Cercle | Géométrie | Ensemble des points équidistants d'un centre | Défini par son rayon ou diamètre |
| Rayon / Diamètre | Géométrie | Rayon : distance centre-bord / Diamètre : 2 × rayon | Si rayon = 5 cm, diamètre = 10 cm |
| Rectangle | Géométrie | Quadrilatère avec 4 angles droits et côtés opposés égaux | Longueur × largeur |
| Losange | Géométrie | Quadrilatère avec 4 côtés égaux et diagonales perpendiculaires | Angles non droits |
| Quadrilatère | Géométrie | Polygone à 4 côtés | Carré, rectangle, losange, trapèze |
| Polygone régulier | Géométrie | Polygone dont tous les côtés et angles sont égaux | Hexagone, pentagone réguliers |
| Parallèle | Géométrie | Droites qui ne se rencontrent jamais | Notation : // |
| Perpendiculaire | Géométrie | Droites qui se coupent à angle droit (90°) | Notation : ⊥ |
| Droite et demi-droite | Géométrie | Droite : illimitée / Demi-droite : un seul côté limité | À distinguer du segment |
| Segment | Géométrie | Portion de droite entre deux points | Notation : [AB] |
| Diagonale | Géométrie | Segment reliant deux sommets non adjacents | Un carré a deux diagonales |
| Intersection | Géométrie | Point(s) commun(s) entre deux figures | Intersection de deux droites, deux cercles |
| Coordonnées | Géométrie | Localisation d'un point dans un repère | Point A(x, y) |
| Abscisse | Géométrie | Coordonnée horizontale (axe x) | Partie x du point (x, y) |
| Ordonnée | Géométrie | Coordonnée verticale (axe y) | Partie y du point (x, y) |
| Ordre croissant / décroissant | Géométrie | Croissant : du plus petit au plus grand / Décroissant : inverse | 1, 2, 3, 5, 8 (croissant) |
| Angle | Géométrie | Ouverture entre deux demi-droites | Aigu (<90°), droit (90°), obtus (>90°) |
| Symétrie axiale / centrale | Géométrie | Axiale : par rapport à une droite / Centrale : par rapport à un point | Figures symétriques |
| Vecteur | Géométrie | Segment orienté avec direction et sens | Représente un déplacement |
| Hypoténuse | Géométrie | Plus grand côté d'un triangle rectangle, opposé à l'angle droit | Dans un triangle 3-4-5, l'hypoténuse est 5 |
| Aire | Géométrie | Surface d'une figure plane | Carré : côté², Rectangle : longueur × largeur |
| Périmètre | Géométrie | Longueur du contour d'une figure | Carré : 4 × côté |
| Calcul statistique | Statistiques et probabilités | Ensemble des méthodes de traitement de données | Moyenne, médiane, écart-type |
| Corrélation | Statistiques et probabilités | Lien entre deux variables | Positive, négative ou nulle |
| Écart type | Statistiques et probabilités | Mesure de dispersion des valeurs autour de la moyenne | Plus l'écart type est grand, plus les données sont dispersées |
| Intervalle de confiance | Statistiques et probabilités | Intervalle dans lequel une valeur a une probabilité de se trouver | 95% de confiance : [valeur min - valeur max] |
| Médiane | Statistiques et probabilités | Valeur centrale d'une série ordonnée | Dans 1, 3, 5, 7, 9 la médiane est 5 |
| Moyenne arithmétique | Statistiques et probabilités | Somme des valeurs divisée par l'effectif | (3+4+5)/3 = 4 |
| Pourcentage | Statistiques et probabilités | Proportion exprimée sur 100 | 25% = 25/100 = 1/4 |
| Mode | Statistiques et probabilités | Valeur la plus fréquente d'une série | Dans 1, 2, 2, 3, 4, 2, le mode est 2 |
| Tableau de fréquence | Statistiques et probabilités | Organisation des valeurs et de leurs effectifs | Valeur | Effectif | Fréquence |
| Expérience aléatoire | Statistiques et probabilités | Expérience dont le résultat n'est pas certain | Lancer de dé, tirage au sort |

Les termes fondamentaux en arithmétique et calcul
Ces brefs rappels3 permettront de sortir de vos blocages en maths et de devenir un bon élève en cours de maths. On ne devient pas le futur Albert Einstein en apprenant par cœur ses définitions, mais on pourra toutefois améliorer ses résultats scolaires !
N°1 - Algèbre
L'algèbre est une branche des mathématiques qui utilise des lettres (généralement x, y, z) pour représenter des quantités inconnues ou variables. Elle permet de généraliser les opérations arithmétiques et de résoudre des problèmes où certaines valeurs sont à déterminer.
Exemple : L'équation 2x + 5 = 13 utilise l'algèbre pour trouver que x = 4.
Vous cherchez à savoir combien de pommes contient un sac fermé. Vous savez que deux sacs identiques plus 5 pommes en vrac font 13 pommes au total. L'algèbre vous aide à calculer qu'un sac contient 4 pommes, sans avoir à l'ouvrir.
L'algèbre transforme les questions arithmétiques concrètes en formules abstraites résolvables de manière systématique. Elle est fondamentale pour toutes les mathématiques avancées.
N°2 - Inconnue
Une inconnue est une valeur que l'on cherche à déterminer dans une équation ou un problème mathématique. Elle est généralement représentée par une lettre, le plus souvent x, y ou z.
Exemple : Dans l'équation x + 3 = 5, l'inconnue x vaut 2.
C'est comme un mystère à résoudre dans un roman policier : vous avez des indices (les nombres et opérations), et vous devez trouver l'identité du coupable (l'inconnue). Tout comme un détective rassemble les pièces du puzzle, vous utilisez les informations données pour découvrir la valeur manquante.
Une équation peut contenir plusieurs inconnues. Dans ce cas, il faut généralement autant d'équations que d'inconnues pour trouver une solution unique.
N°3 - Équation
Une équation est une égalité mathématique contenant une ou plusieurs inconnues. Résoudre une équation signifie trouver la ou les valeurs des inconnues qui rendent l'égalité vraie.
Exemple : 3x - 7 = 8 se résout ainsi :
- 3x - 7 + 7 = 8 + 7
- 3x = 15
- x = 5
Une équation est comme une balance en équilibre. Ce qui est à gauche du signe égal doit avoir le même "poids" que ce qui est à droite. Pour résoudre l'équation, vous effectuez les mêmes opérations des deux côtés pour maintenir l'équilibre tout en isolant l'inconnue.
Elle est à la base de l'histoire des mathématiques.
Il existe différents types d'équations : du premier degré (linéaires), du second degré (quadratiques), exponentielles, etc. Chaque type nécessite des méthodes de résolution spécifiques.
N°4 - Facteur
Un facteur est chacun des nombres ou expressions que l'on multiplie ensemble pour obtenir un produit. Dans une multiplication, tous les éléments multipliés sont des facteurs.
Exemple : Dans 3 × 4 = 12, les nombres 3 et 4 sont les facteurs. Dans l'expression algébrique 5xy, les facteurs sont 5, x et y.
Si vous préparez des tartes pour 3 tables de 4 personnes chacune, le nombre de tables (3) et le nombre de personnes par table (4) sont les deux facteurs qui déterminent le nombre total de parts nécessaires (12).
La factorisation, opération inverse de la multiplication, consiste à décomposer un nombre ou une expression en produit de facteurs. C'est essentiel pour simplifier les calculs et résoudre des équations.
Apprendre vos définitions est déjà un premier pas pour défaire les préjugés liés aux maths.
N°5 - Produit
Le produit est le résultat obtenu après avoir effectué une multiplication. C'est la réponse finale de l'opération.
Exemple : Le produit de 6 et 7 est 42, car 6 × 7 = 42.
Si vous achetez 7 paquets de 6 œufs, le produit (42 œufs au total) représente votre quantité finale. Les paquets et le nombre d'œufs par paquet sont les facteurs, le total d'œufs est le produit.
Les facteurs sont les éléments que l'on multiplie, le produit est le résultat. Le mot "produit" en mathématiques désigne spécifiquement une multiplication, même si dans le langage courant il peut avoir d'autres sens.
Vous en aurez besoin en cours de maths.
N°6 - Somme
La somme est le résultat d'une addition. C'est le total obtenu lorsqu'on ajoute plusieurs nombres ou expressions mathématiques.
Exemple : La somme de 15 et 23 est 38, car 15 + 23 = 38.
Si vous avez 15 euros dans votre poche gauche et 23 euros dans votre poche droite, la somme (38 euros) représente l'argent total dont vous disposez. C'est ce que vous obtiendriez en rassemblant tout votre argent.
En algèbre, une somme peut contenir des termes qu'on ne peut pas additionner directement (comme x + 5). On parle alors de somme algébrique, qui reste sous forme d'expression jusqu'à ce qu'on connaisse la valeur de x.
N°7 - Terme
Un terme est un élément d'une expression algébrique séparé par un signe + ou -. C'est aussi chacun des éléments d'une suite mathématique.
Exemple : Dans l'expression 3x² - 5x + 7, il y a trois termes : 3x², -5x et 7. Dans la suite 2, 4, 6, 8..., le premier terme est 2, le deuxième est 4, etc.
Une expression algébrique est comme une recette. Chaque terme représente un ingrédient différent : vous pouvez avoir des œufs (x²), de la farine (x) et du sucre (nombres seuls). Chaque ingrédient garde son identité dans la liste, même s'ils contribuent tous au résultat final.
Les termes peuvent être "semblables" (ayant la même partie littérale, comme 3x et 5x) ou "non semblables" (comme x² et x). Seuls les termes semblables peuvent être additionnés ou soustraits directement.
N°8 - Différence
La différence est le résultat d'une soustraction. C'est l'écart entre deux nombres ou expressions, obtenu en retranchant le second du premier.
Exemple : La différence entre 50 et 18 est 32, car 50 - 18 = 32.
Si vous aviez 50 euros en début de semaine et qu'il vous en reste 18 en fin de semaine, la différence (32 euros) représente ce que vous avez dépensé. C'est l'écart entre votre situation initiale et finale.
Contrairement à l'addition, l'ordre compte dans une soustraction : 50 - 18 ≠ 18 - 50. La différence peut être négative si on soustrait un nombre plus grand d'un nombre plus petit.
Prêt pour des cours de math 3eme ?
N°9 - Dividende
Le dividende est le nombre que l'on divise dans une opération de division. C'est la quantité initiale que l'on souhaite partager ou répartir.
Exemple : Dans la division 20 ÷ 4 = 5, le nombre 20 est le dividende (4 est le diviseur, 5 est le quotient).
Vous devez partager 20 bonbons entre 4 amis. Les 20 bonbons représentent le dividende, c'est-à-dire ce que vous avez à distribuer au départ.
Dans la notation fractionnaire 20/4, le dividende (20) se trouve au numérateur.
N°10 - Quotient
Le quotient est le résultat d'une division. C'est le nombre de fois qu'un diviseur est contenu dans le dividende.
Exemple : Le quotient de 24 par 6 est 4, car 24 ÷ 6 = 4. Dans la division euclidienne de 17 par 5, le quotient est 3 (avec un reste de 2).
Si vous partagez équitablement 24 cookies entre 6 personnes, le quotient (4) indique combien chaque personne reçoit de cookies. C'est la part individuelle après le partage.
Le quotient peut être un nombre entier, décimal ou fractionnaire selon le type de division effectuée. Dans une division euclidienne (avec des entiers), on distingue le quotient entier du reste éventuel.
N°11 - Numérateur
Le numérateur est le nombre situé au-dessus de la barre de fraction. Il indique combien de parties on considère par rapport au total défini par le dénominateur.
Exemple : Dans la fraction 3/4, le nombre 3 est le numérateur. Il signifie qu'on considère 3 parties sur les 4 qui constituent le tout.
Imaginez une pizza coupée en 4 parts égales. Si vous en mangez 3 parts, vous avez consommé 3/4 de la pizza. Le numérateur (3) compte le nombre de parts que vous avez mangées.
Le numérateur détermine la "quantité" prise, tandis que le dénominateur définit la taille de chaque unité. Pour additionner des fractions, on doit d'abord avoir le même dénominateur, puis on additionne les numérateurs.
N°12 - Dénominateur
Le dénominateur est le nombre situé en-dessous de la barre de fraction. Il indique en combien de parties égales le tout a été divisé.
Exemple : Dans la fraction 5/8, le nombre 8 est le dénominateur. Il signifie que l'unité de référence a été divisée en 8 parts égales.
Si vous coupez un gâteau en 8 parts égales, le dénominateur (8) représente le nombre total de parts disponibles, quelle que soit la quantité que vous allez manger. C'est la "graduation" de votre partage.
Le dénominateur ne peut jamais être zéro (la division par zéro est impossible). Plus le dénominateur est grand, plus chaque part est petite : 1/8 de pizza est plus petit que 1/4 de pizza.
N°13 - Dénominateur commun
Un dénominateur commun est un multiple commun aux dénominateurs de plusieurs fractions, utilisé pour pouvoir les additionner, les soustraire ou les comparer. On cherche généralement le plus petit dénominateur commun (PPCM).
Exemple : Pour additionner 1/3 et 1/4, on utilise 12 comme dénominateur commun : 1/3 = 4/12 et 1/4 = 3/12, donc 1/3 + 1/4 = 7/12.
C'est comme vouloir comparer des pommes et des oranges. Pour savoir si vous avez plus de 1/3 de pomme ou 1/4 d'orange, vous devez les "traduire" dans une unité commune. Le dénominateur commun est cette unité de référence partagée qui permet la comparaison.
Trouver un dénominateur commun revient à "harmoniser" les fractions en les exprimant avec la même subdivision. On peut utiliser n'importe quel multiple commun, mais le PPCM simplifie les calculs.
N°14 - Division euclidienne
La division euclidienne est une division entre deux nombres entiers qui donne un quotient entier et un reste. Elle s'exprime par la relation : dividende = diviseur × quotient + reste, où le reste est plus petit que le diviseur.
Exemple : 17 ÷ 5 donne un quotient de 3 et un reste de 2, car 17 = 5 × 3 + 2.
Vous avez 17 bonbons à distribuer équitablement à 5 enfants. Chaque enfant recevra 3 bonbons (le quotient), et il vous restera 2 bonbons dans le paquet (le reste) que vous ne pouvez pas distribuer équitablement sans les couper.
La division euclidienne est fondamentale en arithmétique et différente de la division décimale. Elle permet de travailler exclusivement avec des nombres entiers et est essentielle pour des concepts comme les nombres premiers ou le PGCD (plus grand commun diviseur).
N°15 - Fraction
Une fraction exprime un rapport entre deux nombres entiers : le numérateur (nombre du haut) et le dénominateur (nombre du bas). Elle représente une partie d'un tout ou un quotient.
Exemple : 3/5 signifie 3 parties sur 5, ou encore 3 divisé par 5, ce qui équivaut à 0,6 en notation décimale.
Quand vous partagez une tablette de chocolat en 5 carrés égaux et que vous en prenez 3, vous possédez 3/5 de la tablette. La fraction quantifie précisément votre part par rapport au tout.
Les fractions peuvent être simplifiées en divisant numérateur et dénominateur par leur PGCD. Une fraction où le numérateur est plus grand que le dénominateur (comme 7/3) représente un nombre supérieur à 1.
N°16 - Nombre
Un nombre est un concept mathématique permettant de quantifier, compter, mesurer ou ordonner. Les nombres peuvent être classés en différentes catégories selon leurs propriétés. Voici le différents types de nombres :
Nombres naturels (ℕ)
0, 1, 2, 3... (entiers positifs)
Nombres entiers relatifs (ℤ)
..., -2, -1, 0, 1, 2... (avec les négatifs)
Nombres rationnels (ℚ)
Tous les nombres exprimables sous forme de fraction
Nombres réels (ℝ)
Incluent rationnels et irrationnels (comme π ou √2)
Nombres décimaux
Peuvent s'écrire avec un nombre fini de chiffres après la virgule
Les nombres sont comme un langage universel pour décrire le monde. Vous utilisez des nombres naturels pour compter vos amis, des décimaux pour mesurer votre taille (1,75 m), des négatifs pour la température (-5°C), et des rationnels pour les proportions (1/2 cuillère de sel).
Tous les nombres ne sont pas interchangeables dans tous les contextes. On ne peut pas avoir -3 personnes dans une pièce, mais -3°C a du sens pour une température.
N°17 - Nombres premiers
Un nombre premier est un nombre entier naturel supérieur à 1 qui n'est divisible que par 1 et par lui-même. Il possède exactement deux diviseurs.
Exemples : 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31... Le nombre 2 est le seul nombre premier pair. Le nombre 1 n'est pas considéré comme premier.
Contre-exemples : 4 (divisible par 1, 2 et 4), 6 (divisible par 1, 2, 3 et 6), 9 (divisible par 1, 3 et 9) ne sont pas premiers.
Les nombres premiers sont comme les "atomes" des mathématiques : ils sont indivisibles et tous les autres nombres peuvent être construits en les multipliant ensemble. C'est pourquoi on les appelle les "briques élémentaires" de l'arithmétique.
Il existe une infinité de nombres premiers. Ils jouent un rôle crucial en cryptographie moderne (sécurité des transactions bancaires en ligne). La décomposition en facteurs premiers est unique pour chaque nombre.
N°18 - Nombre naturel
Les nombres naturels sont les nombres entiers positifs utilisés pour compter : 0, 1, 2, 3, 4, 5... L'ensemble des nombres naturels est noté ℕ (ℕ* exclut le zéro selon les conventions).
Exemple : Quand vous comptez des objets (5 pommes, 12 élèves, 100 pages), vous utilisez des nombres naturels. Vous ne pouvez pas avoir 3,5 voitures dans un parking ou -2 chaises dans une classe.
Les nombres naturels sont ceux qu'un enfant apprend en premier pour compter sur ses doigts. Ce sont les nombres "évidents" du quotidien, ceux qui répondent à la question "combien ?" pour des objets entiers et concrets.
Les nombres naturels sont infinis (il n'existe pas de plus grand nombre naturel). Ils sont stables par addition et multiplication (la somme ou le produit de deux nombres naturels est toujours un nombre naturel), mais pas par soustraction (5 - 7 n'est pas naturel).
N°19 - Multiplicateur
Le multiplicateur est le nombre par lequel on multiplie une quantité. Dans une multiplication a × b, si on considère a comme la quantité de base, b est le multiplicateur qui indique combien de fois on prend cette quantité.
Exemple : Dans 7 × 3 = 21, si 7 représente le nombre d'objets dans un groupe, alors 3 est le multiplicateur qui indique qu'on a 3 groupes identiques.
Si le prix d'un café est de 2 € et que vous en achetez 4, le multiplicateur (4) indique combien de fois vous répétez l'achat du café à 2 €. Votre dépense totale est 2 € × 4 = 8 €.
La distinction entre multiplicateur et facteur est subtile : tous deux sont des facteurs dans une multiplication, mais on parle spécifiquement de multiplicateur quand on met l'accent sur l'action de répéter ou d'augmenter une quantité. En algèbre, dans 5x, le nombre 5 est le coefficient multiplicateur de la variable x.
N°20 - PGCD (Plus Grand Commun Diviseur)
Le PGCD de deux ou plusieurs nombres entiers est le plus grand nombre qui divise simultanément tous ces nombres sans laisser de reste.
Exemple : Le PGCD de 24 et 36 est 12, car :
Diviseurs de 24
1, 2, 3, 4, 6, 8, 12, 24
Diviseurs de 36
1, 2, 3, 4, 6, 9, 12, 18, 36
Diviseurs communs
1, 2, 3, 4, 6, 12
Le plus grand est
12
Vous voulez organiser 24 pommes et 36 oranges en paquets identiques contenant le même nombre de pommes et d'oranges, sans reste. Le PGCD (12) vous indique que vous pouvez faire au maximum 12 paquets (chacun contiendra 2 pommes et 3 oranges).
Le PGCD est essentiel pour simplifier des fractions : on divise le numérateur et le dénominateur par leur PGCD. L'algorithme d'Euclide permet de calculer efficacement le PGCD de deux grands nombres.
N°21 - Puissance
Une puissance est le résultat d'une multiplication répétée d'un nombre (la base) par lui-même un certain nombre de fois (l'exposant). Elle s'écrit sous la forme aⁿ, où a est la base et n l'exposant.
Exemples :
2⁴
2 × 2 × 2 × 2 = 16
(on dit "2 puissance 4" ou "2 exposant 4")
5³
5 × 5 × 5 = 125
10²
100
Si vous partagez un message à 3 amis sur un réseau social, qui chacun le partagent à 3 autres amis, qui font de même... Après 4 "générations", le message a atteint 3⁴ = 81 personnes. L'exposant représente le nombre de fois que le processus se répète.
Les propriétés des puissances facilitent les calculs : aᵐ × aⁿ = aᵐ⁺ⁿ, (aᵐ)ⁿ = aᵐˣⁿ, a⁰ = 1 (pour a ≠ 0), et a⁻ⁿ = 1/aⁿ.
N°22 - Racine carrée
La racine carrée d'un nombre positif est le nombre qui, multiplié par lui-même, donne ce nombre. Elle est notée √ et représente l'opération inverse de l'élévation au carré.
Exemples :
- √9 = 3, car 3 × 3 = 9
- √16 = 4, car 4 × 4 = 16
- √2 ≈ 1,414... (nombre irrationnel)
Si vous connaissez l'aire d'un carré (25 m²) et que vous voulez connaître la longueur d'un côté, vous calculez √25 = 5 m. La racine carrée "défait" l'opération du carré : elle vous ramène du "résultat" (surface) à la "cause" (côté).
La racine carrée n'existe que pour les nombres positifs dans l'ensemble des réels. √(a × b) = √a × √b, mais √(a + b) ≠ √a + √b. Le symbole √ désigne toujours la racine carrée positive (racine principale).
N°23 - Priorité des opérations
La priorité des opérations est l'ordre dans lequel on effectue les calculs dans une expression mathématique. Cet ordre suit une convention universelle pour éviter les ambiguïtés.
Ordre de priorité (PEMDAS en anglais, ou règle des priorités) :
P
Parenthèses
(et crochets, accolades)
E
Exposants
(puissances et racines)
M et D
Multiplication et Division
(de gauche à droite)
A et S
Addition et Soustraction
(de gauche à droite)
Exemple : Calculons 3 + 4 × 2² - (8 - 3)
- Parenthèses d'abord : (8 - 3) = 5 → 3 + 4 × 2² - 5
- Puissances : 2² = 4 → 3 + 4 × 4 - 5
- Multiplication : 4 × 4 = 16 → 3 + 16 - 5
- Addition et soustraction : 3 + 16 = 19, puis 19 - 5 = 14
C'est comme suivre une recette de cuisine : vous ne pouvez pas mélanger tous les ingrédients au hasard. Vous devez d'abord préchauffer le four (parenthèses), préparer la base (puissances), mélanger certains ingrédients ensemble (multiplication/division), et enfin assembler le tout (addition/soustraction).
Sans respecter les priorités, 3 + 4 × 2 pourrait donner 14 (faux, si on fait de gauche à droite) au lieu de 11 (correct). Les parenthèses permettent de modifier l'ordre : (3 + 4) × 2 = 14.
N°24 - Diviseur
Un diviseur d'un nombre entier est un nombre qui divise ce nombre sans laisser de reste. Autrement dit, a est un diviseur de b si b est un multiple de a.
Exemple : Les diviseurs de 12 sont : 1, 2, 3, 4, 6 et 12, car :
- 12 ÷ 1 = 12
- 12 ÷ 2 = 6
- 12 ÷ 3 = 4
- 12 ÷ 4 = 3
- 12 ÷ 6 = 2
- 12 ÷ 12 = 1
Si vous devez ranger 12 livres sur des étagères et que vous voulez le même nombre de livres par étagère (sans laisser de livre à part), vous pouvez utiliser 1, 2, 3, 4, 6 ou 12 étagères. Ces nombres sont les diviseurs de 12 : ils "divisent" parfaitement votre collection.
Tout nombre a au moins deux diviseurs : 1 et lui-même. Les nombres n'ayant que ces deux diviseurs sont des nombres premiers. Le diviseur d'un nombre dans une division est le nombre par lequel on divise (à ne pas confondre avec le dividende).
N°25 - Carré magique
Un carré magique est une grille carrée de nombres où la somme des nombres de chaque ligne, de chaque colonne et de chaque diagonale est identique. Cette somme constante s'appelle la "constante magique".
Exemple :
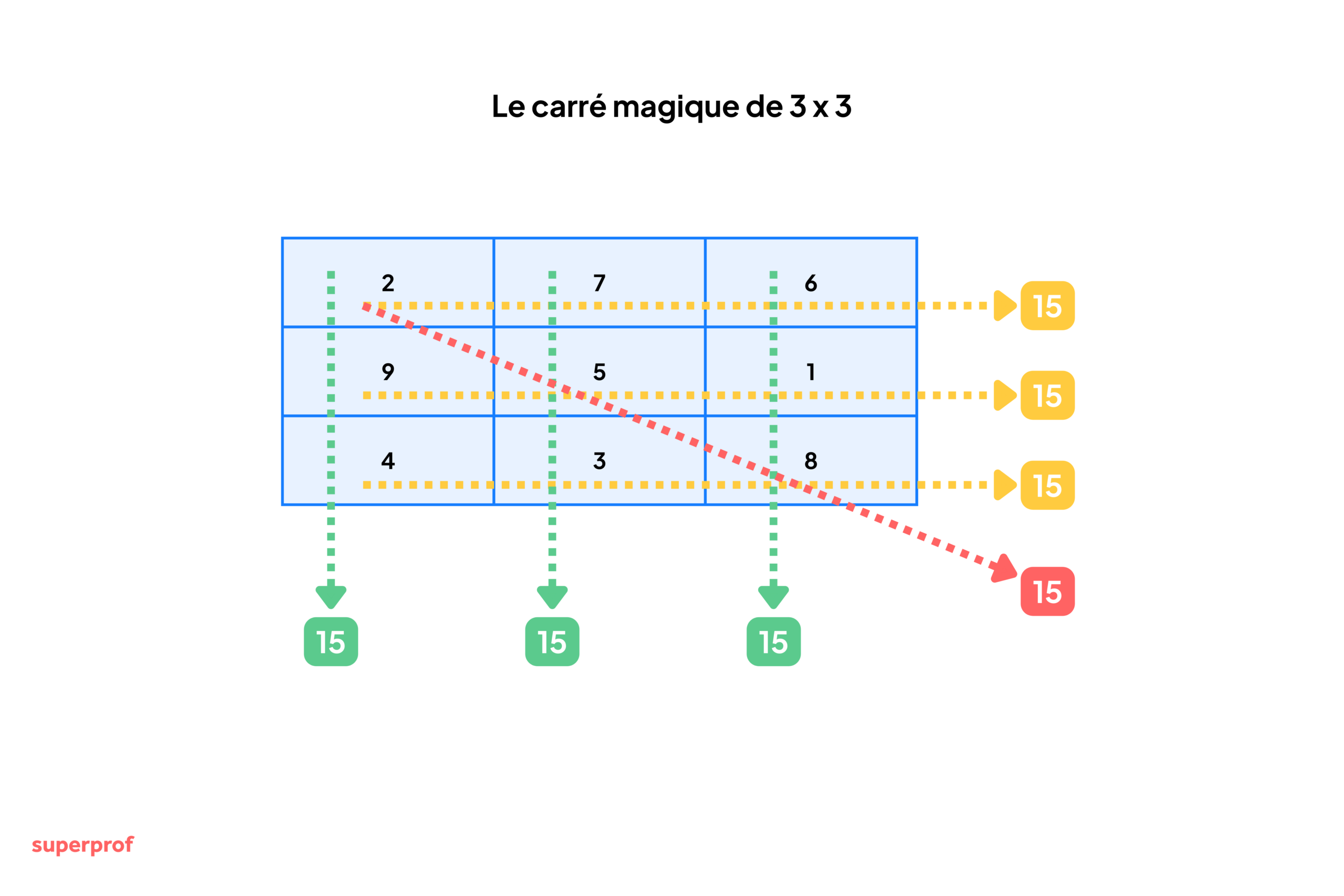
Chaque ligne, colonne et diagonale donne 15 (la constante magique).
C'est comme un puzzle numérique où vous devez équilibrer parfaitement tous les côtés et les diagonales. Vous distribuez des cartes à des joueurs : chaque rangée représente un joueur, et le carré magique garantit que tous reçoivent exactement la même valeur totale, quelle que soit la manière de compter.
Les carrés magiques existent en différentes tailles (3×3, 4×4, 5×5...). Ils ont fasciné les mathématiciens depuis l'Antiquité et ont des applications en combinatoire. La constante magique d'un carré n×n utilisant les nombres de 1 à n² est : n(n² + 1)/2.
Le vocabulaire mathématique en géométrie
Continuons avec des définitions liées à la géométrie et qui vous seront bien utiles pour voir les liens entre les maths et la peinture.
N°26 - Géométrie
La géométrie est la branche des mathématiques qui étudie les formes, les dimensions, les positions et les propriétés de l'espace. Elle analyse les figures, leurs mesures, leurs relations et leurs transformations.
Principales branches :
Géométrie plane
Etudie les figures à deux dimensions
(triangles, cercles, polygones)
Géométrie dans l'espace
Etudie les solides à trois dimensions
(cubes, sphères, pyramides)
Géométrie analytique
Utilise les coordonnées et l'algèbre pour étudier les figures
Géométrie euclidienne
Basée sur les postulats d'Euclide
(la géométrie "classique")
La géométrie est partout autour de vous : l'architecture des bâtiments, le design des objets, les panneaux de signalisation, les terrains de sport. Quand vous mesurez votre pièce pour y installer un meuble ou calculez le chemin le plus court vers un lieu, vous faites de la géométrie appliquée.
La géométrie combine intuition visuelle et rigueur logique. Elle est fondamentale en architecture, ingénierie, design, physique et même dans les arts graphiques et l'informatique.
Comprendre la géométrie permet ainsi de découvrir les liens qui existent entre les maths et l'informatique.
N°27 - Triangle
Un triangle est un polygone à trois côtés, trois sommets et trois angles. La somme de ses angles intérieurs est toujours égale à 180°.
Types de triangles selon les côtés :
- Équilatéral : trois côtés égaux, trois angles de 60°
- Isocèle : deux côtés égaux, deux angles égaux
- Scalène : trois côtés de longueurs différentes
Types de triangles selon les angles :
- Rectangle : possède un angle droit (90°)
- Acutangle : tous les angles sont aigus (< 90°)
- Obtusangle : possède un angle obtus (> 90°)
Le triangle est la forme la plus stable en construction. Les ponts, les toits de maisons, les grues utilisent des triangles car cette forme rigide ne se déforme pas sous la pression, contrairement à un carré qui pourrait devenir un losange.
Le triangle est la figure la plus simple après le segment. L'aire d'un triangle se calcule avec la formule : (base × hauteur) ÷ 2. Le théorème de Pythagore s'applique aux triangles rectangles : a² + b² = c².
Connaissez-vous ces 7 exemples surprenants d'utilisation des maths ?
N°28 - Carré
Un carré est un quadrilatère régulier ayant quatre côtés de même longueur et quatre angles droits (90°). C'est à la fois un rectangle particulier (avec tous les côtés égaux) et un losange particulier (avec des angles droits).
Propriétés du carré :
- Tous les côtés sont égaux
- Tous les angles sont droits
- Les diagonales sont égales, perpendiculaires et se coupent en leur milieu
- Il possède 4 axes de symétrie
Formules :
Périmètre = 4 × côté
Aire = côté²
Le carré est omniprésent : les carreaux de carrelage, les post-it, les échiquiers, les cases de mots croisés. Sa forme régulière le rend facile à agencer et à reproduire, d'où son utilisation massive dans les pavages et quadrillages.
Le carré est la figure plane régulière à 4 côtés. Sa diagonale mesure côté × √2 (environ 1,41 fois le côté). C'est l'un des trois polygones réguliers pouvant paver le plan seul sans espaces ni chevauchement (avec le triangle équilatéral et l'hexagone).
N°29 - Cercle
Un cercle est l'ensemble de tous les points situés à une même distance (le rayon) d'un point fixe (le centre). C'est une ligne courbe fermée parfaitement ronde.
Éléments du cercle :
Centre
Point de référence
Rayon
Distance du centre à n'importe quel point du cercle
Diamètre
Segment passant par le centre et reliant deux points du cercle
(= 2 × rayon)
Circonférence
Longueur du contour du cercle
Disque
Surface délimitée par le cercle (intérieur inclus)
Formules :
Circonférence = 2 × π × rayon (ou π × diamètre)
Aire du disque = π × rayon²

Le cercle est la forme parfaite de la nature : bulles de savon, iris de l'œil... C'est la forme qui offre le plus grand espace pour un périmètre donné, d'où son utilisation pour les pizzas, assiettes et pièces de monnaie.
Le nombre π (pi) ≈ 3,14159... est le rapport constant entre la circonférence et le diamètre de tout cercle. Le cercle a une infinité d'axes de symétrie passant par son centre.
N°30 - Rayon / Diamètre
Le rayon d'un cercle est la distance entre le centre du cercle et n'importe quel point situé sur le cercle. Tous les rayons d'un même cercle ont la même longueur.
Le diamètre est un segment qui passe par le centre du cercle et relie deux points du cercle. C'est le plus grand segment qu'on peut tracer dans un cercle.
Diamètre = 2 × Rayon, ou Rayon = Diamètre ÷ 2
Si vous plantez un piquet au centre d'un jardin et que vous y attachez une corde de 5 mètres, en tendant cette corde et en tournant autour du piquet, vous tracerez un cercle. La corde représente le rayon (5 m), et si vous mesurez le jardin circulaire d'un bout à l'autre en passant par le piquet, vous obtiendrez le diamètre (10 m).
Dans toutes les formules du cercle (aire, circonférence), on peut utiliser soit le rayon, soit le diamètre, mais le rayon est généralement privilégié car il représente la distance fondamentale depuis le centre.
N°31 - Rectangle
Un rectangle est un quadrilatère ayant quatre angles droits (90°). Ses côtés opposés sont parallèles et de même longueur. On distingue généralement la longueur (le grand côté) de la largeur (le petit côté).
Propriétés du rectangle :
- Quatre angles droits
- Côtés opposés égaux et parallèles
- Diagonales égales qui se coupent en leur milieu
- 2 axes de symétrie (sauf pour le carré qui en a 4)
Formules :
Périmètre = 2 × (longueur + largeur)
Aire = longueur × largeur
Le rectangle est une forme géométrique très utilisée dans notre environnement : feuilles de papier, écrans de télévision ou d'ordinateur, portes, fenêtres, livres, téléphones... Sa forme allongée est pratique pour la lecture et l'organisation visuelle.
Le carré est un rectangle particulier où longueur = largeur. Le rectangle est facile à construire avec une règle et une équerre, ce qui explique sa popularité en architecture et menuiserie.
N°32 - Losange
Un losange est un quadrilatère dont les quatre côtés ont la même longueur. Contrairement au carré, ses angles ne sont pas nécessairement droits (sauf si c'est un carré, qui est un losange particulier).
Propriétés du losange :
- Quatre côtés égaux
- Côtés opposés parallèles
- Angles opposés égaux
- Diagonales perpendiculaires qui se coupent en leur milieu
- 2 axes de symétrie (le long des diagonales)
Formule de l'aire : Aire = (grande diagonale × petite diagonale) ÷ 2
Pensez aux carreaux de carrelage posés "en pointe" (à 45°), ou au symbole des carreaux dans un jeu de cartes (♦). Le losange apparaît aussi dans les panneaux de signalisation routière et dans les motifs décoratifs textiles (losanges imbriqués).
Un losange "écrasé" (très aplati) reste un losange tant que les quatre côtés sont égaux. Le parallélogramme est plus général (côtés opposés égaux), tandis que le losange exige que tous les côtés soient égaux.
N°33 - Quadrilatère
Un quadrilatère est un polygone à quatre côtés, quatre sommets et quatre angles. La somme de ses angles intérieurs est toujours égale à 360°.
Principaux types de quadrilatères :
Trapèze
Au moins deux côtés parallèles
Parallélogramme
Côtés opposés parallèles
Rectangle
Parallélogramme avec angles droits
Losange
Parallélogramme avec côtés égaux
Carré
Rectangle et losange à la fois
Cerf-volant
Deux paires de côtés adjacents égaux
Les quadrilatères sont partout dans l'architecture et le design : tables, champs agricoles, terrains de sport. Même les formes "irrégulières" d'une parcelle de terrain ou d'une pièce de puzzle à 4 côtés sont des quadrilatères.
Tout quadrilatère peut être divisé en deux triangles en traçant une diagonale. C'est pourquoi la somme de ses angles est 360° (deux fois 180°). Les quadrilatères convexes ont tous leurs angles inférieurs à 180°.
N°34 - Polygone régulier
Un polygone régulier est un polygone dont tous les côtés ont la même longueur et tous les angles ont la même mesure. Il est à la fois équilatéral (côtés égaux) et équiangle (angles égaux).
Exemples :
Triangle équilatéral
3 côtés, angles de 60°
Carré
4 côtés, angles de 90°
Pentagone régulier
5 côtés, angles de 108°
Hexagone régulier
6 côtés, angles de 120°
Octogone régulier
8 côtés, angles de 135°
Forme des panneaux Stop
Les alvéoles d'une ruche d'abeilles forment des hexagones réguliers. Les écrous et boulons sont souvent hexagonaux. Les ballons de football traditionnels utilisent des pentagones et hexagones réguliers. Ces formes combinent efficacité et esthétique.
La formule pour calculer chaque angle intérieur d'un polygone régulier à n côtés est : [(n-2) × 180°] ÷ n. Un polygone régulier peut être inscrit dans un cercle (tous ses sommets touchent le cercle).
N°35 - Parallèle
Deux droites sont parallèles si elles sont situées dans le même plan et ne se rencontrent jamais, quelle que soit leur prolongation. Elles maintiennent toujours la même distance entre elles.
On note (d) // (d') pour dire que les droites d et d' sont parallèles.
Propriétés :
- Deux droites perpendiculaires à une même troisième droite sont parallèles entre elles
- Si deux droites sont coupées par une sécante, et que les angles correspondants sont égaux, alors les droites sont parallèles
Les rails d'un chemin de fer sont parallèles : ils ne se rencontrent jamais et restent à distance constante pour permettre au train de circuler. Les lignes d'un cahier d'écolier, les bords opposés d'une règle, les lignes blanches sur une route sont d'autres exemples de parallélisme.
En géométrie euclidienne (la géométrie "classique"), par un point extérieur à une droite passe une unique droite parallèle à cette droite (axiome des parallèles). Dans un parallélogramme, les côtés opposés sont parallèles.
N°36 - Perpendiculaire
Deux droites sont perpendiculaires si elles se coupent en formant un angle droit (90°). Leur intersection crée quatre angles droits.
On note (d) ⊥ (d') pour indiquer que les droites d et d' sont perpendiculaires.
Propriétés :
- Si deux droites sont perpendiculaires à une même troisième droite, elles sont parallèles entre elles
- La hauteur d'un triangle est perpendiculaire à la base
- Les diagonales d'un losange sont perpendiculaires
L'équerre de votre trousse est conçue pour tracer des perpendiculaires. Les intersections en croix dans une ville (rues se croisant à angle droit), les angles d'un cadre photo rectangulaire, ou encore le T formé par un mur et le sol sont des perpendiculaires.
La perpendicularité est essentielle en construction : les murs doivent être perpendiculaires au sol pour la stabilité. En géométrie analytique, deux droites de pentes m₁ et m₂ sont perpendiculaires si m₁ × m₂ = -1.
N°37 - Droite et demi-droite
Une droite est une ligne parfaitement rectiligne, sans épaisseur, qui s'étend infiniment dans les deux directions. Elle contient une infinité de points alignés.
Une droite se note (AB) ou (d).
Une demi-droite est une portion de droite limitée d'un côté par un point (l'origine) et qui s'étend infiniment dans une seule direction.
Une demi-droite d'origine A passant par B se note [AB).
Si un rayon laser peut traverser infiniment l'espace dans les deux sens, c'est une droite. Si le laser part d'un projecteur (point d'origine) et ne va que dans une direction, c'est une demi-droite. La différence entre une droite et une demi-droite est comme celle entre une route sans fin et une autoroute qui part d'un péage mais n'a qu'une seule direction.
Une droite n'a ni début ni fin, une demi-droite a un début (origine) mais pas de fin, et un segment a à la fois un début et une fin. Deux points déterminent une unique droite.
N°38 - Segment
Un segment est la portion de droite limitée par deux points appelés extrémités. Contrairement à la droite ou la demi-droite, le segment a une longueur finie et mesurable.
Le segment d'extrémités A et B se note [AB]. Sa longueur se note AB (sans crochets).
Propriétés :
- Un segment possède un milieu, point équidistant des deux extrémités
- La longueur d'un segment est la distance entre ses extrémités
- Un segment est la plus courte distance entre deux points
Tous les objets rectilignes de taille finie sont des segments : un crayon, le côté d'une table, une règle graduée, le trait que vous tracez entre deux points sur une feuille. C'est la "vraie" ligne que vous pouvez physiquement mesurer et tracer.
Le segment [AB] est identique au segment [BA] (même longueur, mêmes extrémités). Le milieu M d'un segment [AB] vérifie AM = MB = AB/2. Les segments sont les éléments de base pour construire toutes les figures géométriques.
N°39 - Diagonale
Une diagonale est un segment qui relie deux sommets non consécutifs d'un polygone. Dans un polygone à n côtés, il existe n(n-3)/2 diagonales.
Exemples :
Triangle
0 diagonale (tous les sommets sont adjacents)
Quadrilatère
2 diagonales
Pentagone
5 diagonales
Hexagone
9 diagonales
Propriétés selon les figures :
- Dans un rectangle, les diagonales sont égales
- Dans un losange, les diagonales sont perpendiculaires
- Dans un carré, les diagonales sont égales et perpendiculaires
Quand vous coupez un sandwich carré en deux triangles de coin à coin, vous suivez la diagonale. Dans un terrain de football rectangulaire, la distance d'un coin à celui diagonalement opposé est plus longue que les côtés : c'est la diagonale.
Les diagonales d'un parallélogramme se coupent en leur milieu. La diagonale d'un carré de côté c mesure c√2 (environ 1,41 × c).
N°40 - Intersection
L'intersection de deux figures géométriques est l'ensemble des points qui appartiennent simultanément aux deux figures. C'est leur "zone de rencontre".
Exemples :
Intersection de deux droites
Généralement un point
(ou aucun si elles sont parallèles, ou une infinité si elles sont confondues)
Intersection de deux cercles
Deux points, un point (cercles tangents), ou aucun point
Intersection d'une droite et d'un cercle
Deux points, un point (tangente), ou aucun point
On utilise le symbole ∩. Par exemple, A ∩ B désigne l'intersection des ensembles A et B.
L'intersection de deux rues est l'endroit où elles se croisent. Quand deux poutres se rencontrent dans une charpente, leur intersection est le point de contact.
Deux droites dans un plan soit se coupent en un point (intersection), soit sont parallèles (pas d'intersection), soit sont confondues (intersection = toute la droite). L'intersection peut être vide, finie ou infinie selon les figures.
Découvrez aussi l'évolution des maths lors des siècles derniers...
N°41 - Coordonnées
Les coordonnées d'un point dans un plan sont deux nombres qui permettent de localiser précisément ce point par rapport à un repère. Dans un repère cartésien, on utilise une paire (x, y) appelée couple de coordonnées.
Système de coordonnées cartésien :
Origine
Point de référence noté O (0, 0)
Axe des abscisses
Axe horizontal
Axe des ordonnées
Axe vertical
Point M(x, y)
x est l'abscisse, y est l'ordonnée
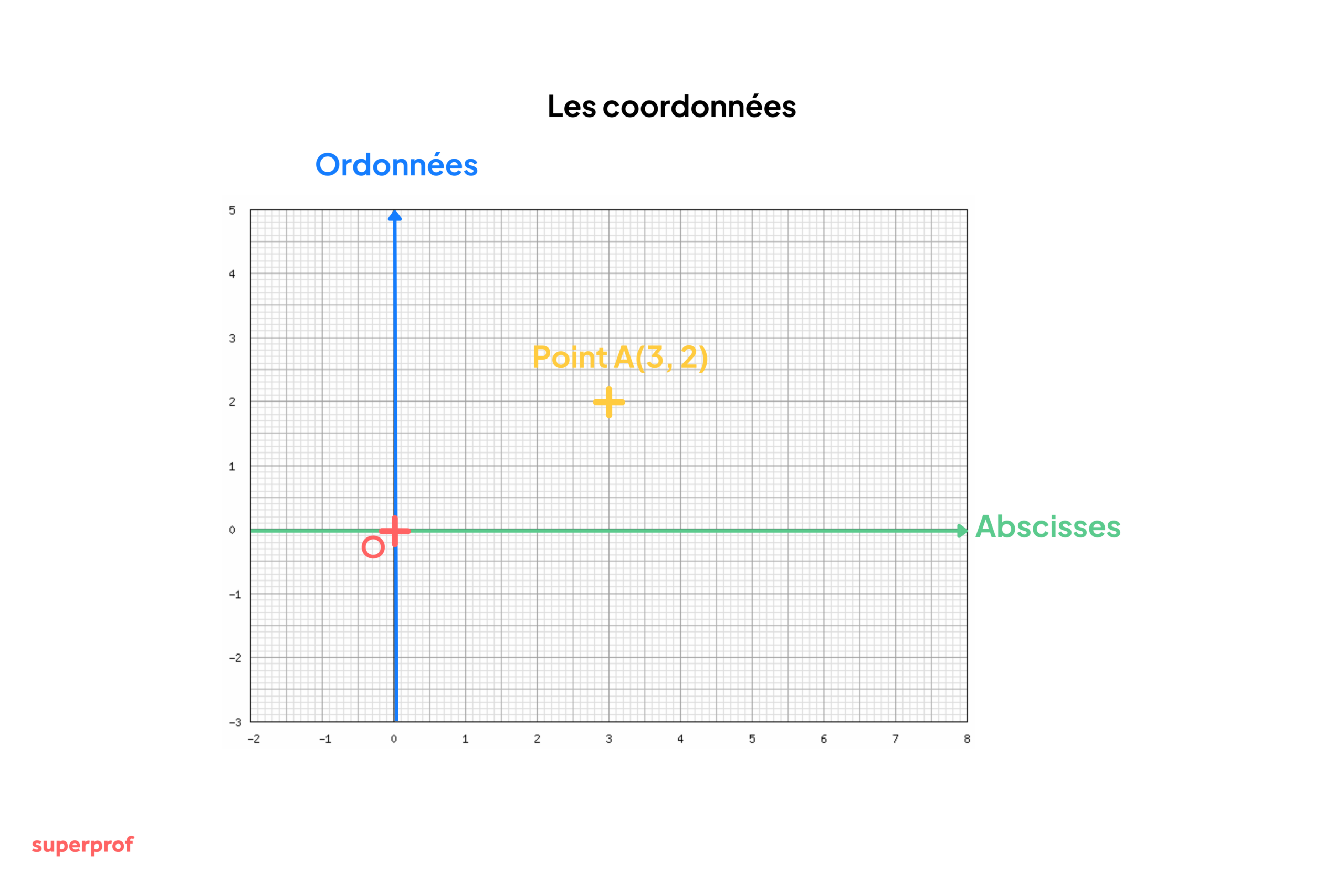
Les coordonnées fonctionnent comme le jeu de la bataille navale : pour localiser un bateau, vous donnez une lettre (colonne) et un chiffre (ligne). Dans une ville quadrillée comme New York, "l'angle de la 5ème avenue et de la 42ème rue" utilise un système de coordonnées. Le GPS de votre téléphone utilise également des coordonnées (latitude et longitude).
Dans un repère orthonormé, les axes sont perpendiculaires et les unités sont les mêmes sur les deux axes. La distance entre deux points A(x₁, y₁) et B(x₂, y₂) se calcule par : √[(x₂-x₁)² + (y₂-y₁)²].
N°42 - Abscisse
L'abscisse est la coordonnée horizontale d'un point dans un repère cartésien. C'est le premier nombre du couple de coordonnées (x, y), qui indique la position du point le long de l'axe horizontal.
Abscisse positive
A droite de l'origine
Abscisse négative
A gauche de l'origine
Abscisse nulle
Sur l'axe des ordonnées (axe vertical)
Exemple : Dans le point M(4, -2), l'abscisse est 4, ce qui signifie que M se trouve 4 unités à droite de l'origine.
Sur une carte routière, si l'origine est votre maison, l'abscisse indique de combien de kilomètres vous devez vous déplacer vers l'est (positif) ou l'ouest (négatif). C'est comme la première instruction : "aller à droite ou à gauche".
Le terme "abscisse" vient du latin abscissa (coupée), car elle "coupe" l'axe horizontal.
N°43 - Ordonnée
L'ordonnée est la coordonnée verticale d'un point dans un repère cartésien. C'est le second nombre du couple de coordonnées (x, y), qui indique la position du point le long de l'axe vertical.
Ordonnée positive
Au-dessus de l'origine
Ordonnée négative
En-dessous de l'origine
Ordonnée nulle
Sur l'axe des abscisses (axe horizontal)
Exemple : Dans le point P(-3, 7), l'ordonnée est 7, ce qui signifie que P se trouve 7 unités au-dessus de l'origine.
Dans un immeuble, l'ordonnée serait l'étage où vous allez : sous-sol (négatif), rez-de-chaussée (zéro), ou étages supérieurs (positif). C'est la dimension verticale, comme l'altitude sur une carte topographique.
L'ordonnée correspond toujours à l'axe vertical (axe des y ou axe Oy). Tous les points situés sur une même horizontale ont la même ordonnée. Sur un graphique de fonction y = f(x), l'ordonnée représente la valeur de la fonction.
N°44 - Ordre croissant / décroissant
Une suite de nombres est en ordre croissant si chaque terme est supérieur ou égal au précédent. Les valeurs augmentent (ou restent égales) de gauche à droite.
Exemple : 2, 5, 7, 11, 11, 15
Une suite de nombres est en ordre décroissant si chaque terme est inférieur ou égal au précédent. Les valeurs diminuent (ou restent égales) de gauche à droite.
Exemple : 20, 18, 15, 9, 3
Classer des personnes par ordre croissant de taille signifie les ranger de la plus petite à la plus grande. Les prix sur un menu de restaurant sont souvent en ordre croissant (entrées, puis plats, puis desserts de plus en plus chers). Un thermomètre qui monte montre une température en ordre croissant.
On utilise strictement croissant pour dire que chaque terme est strictement supérieur au précédent (pas d'égalité possible).
N°45 - Angle
Un angle est une figure géométrique formée par deux demi-droites (appelées côtés) ayant la même origine (appelée sommet). L'angle mesure l'écart entre ces deux demi-droites.
Types d'angles selon leur mesure :
Angle aigu
Entre 0° et 90°
Angle droit
Exactement 90° (noté par un petit carré)
Angle obtus
Entre 90° et 180°
Angle plat
Exactement 180° (une ligne droite)
Angle rentrant
Entre 180° et 360°
L'angle de sommet B formé par les demi-droites [BA) et [BC) se note ∠ABC ou B̂.
Quand vous ouvrez une porte, l'angle entre la porte et le mur change : légèrement ouverte (angle aigu), perpendiculaire au mur (angle droit), grande ouverte (angle obtus). Les aiguilles d'une horloge forment différents angles selon l'heure. L'ouverture d'un compas dessine un angle.
Un angle complet (tour entier) fait 360°. Deux angles sont complémentaires si leur somme vaut 90°, supplémentaires si leur somme vaut 180°. L'angle ne dépend pas de la longueur des côtés, mais seulement de leur écartement.
Prêt pour un cours de math 3eme ?
N°46 - Symétrie axiale / centrale
Une figure possède une symétrie axiale par rapport à une droite (axe de symétrie) si elle se superpose à elle-même par pliage le long de cet axe. Chaque point de la figure a un point symétrique de l'autre côté de l'axe, à égale distance.
Exemples : papillon (axe vertical), visage humain (approximativement), lettre A, cœur
Une figure possède une symétrie centrale par rapport à un point (centre de symétrie) si elle se superpose à elle-même par rotation de 180° autour de ce point. Chaque point de la figure a un point symétrique diamétralement opposé.
Exemples : lettre S, Z, N, symbole yin-yang, carte à jouer
Votre visage présente une symétrie axiale approximative (axe vertical séparant gauche et droite) : vos yeux, oreilles et joues sont disposés symétriquement de part et d'autre du nez. Quand vous vous regardez dans un miroir, vous voyez votre symétrique par rapport au plan du miroir.
Un carré possède 4 axes de symétrie et 1 centre de symétrie. Un rectangle non carré a 2 axes de symétrie mais 1 centre. Un cercle a une infinité d'axes de symétrie et un centre. Les symétries sont des transformations géométriques qui préservent les distances.
N°47 - Vecteur
Un vecteur est un objet mathématique caractérisé par une direction, un sens et une longueur (appelée norme ou module). On le représente graphiquement par une flèche.
Un vecteur se note généralement avec une flèche au-dessus :
(vecteur du point A vers le point B).

Dans un repère, un vecteur
peut être défini par ses coordonnées (x, y), qu'on note aussi
.
Propriétés :
- Deux vecteurs sont égaux s'ils ont même direction, même sens et même norme (peu importe leur position)
- On peut additionner des vecteurs, les multiplier par un nombre
Quand un GPS vous dit "allez vers le nord pendant 3 km", il décrit un vecteur : une direction (nord), un sens (vers le nord, pas vers le sud), et une distance (3 km). Le vent est aussi un vecteur : il a une direction, souffle dans un sens, et a une force. Un déplacement physique est toujours un vecteur.
Les vecteurs sont fondamentaux en physique (forces, vitesses, accélérations) et en géométrie. Contrairement à un point qui a une position fixe, un vecteur représente un déplacement ou une grandeur orientée, indépendant du point de départ.
N°48 - Hypoténuse
L'hypoténuse est le côté le plus long d'un triangle rectangle. C'est le côté opposé à l'angle droit, qui relie les deux côtés perpendiculaires (appelés cathètes).
Théorème de Pythagore : Dans un triangle rectangle, le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés : a² + b² = c² (où c est l'hypoténuse et a, b les cathètes).
Exemple : Dans un triangle rectangle avec des cathètes de 3 cm et 4 cm, l'hypoténuse mesure 5 cm, car 3² + 4² = 9 + 16 = 25 = 5².
Vous voulez traverser un parc rectangulaire en diagonale au lieu de longer les côtés. Si le parc fait 30 m de large et 40 m de long, la diagonale (qui est l'hypoténuse du triangle formé) mesure √(30² + 40²) = √2 500 = 50 m. Vous économisez donc 20 m par rapport au chemin de 70 m en suivant les bords !
En trigonométrie, l'hypoténuse sert de référence pour calculer sinus et cosinus.
N°49 - Aire
L'aire représente la surface qu'occupe une figure plane, mesurée en unités carrées (cm², m², km²). C'est l'espace bidimensionnel délimité par le contour d'une forme géométrique.
Formules principales :
Rectangle
Longueur × Largeur
Triangle
(Base × Hauteur) ÷ 2
Carré
Côté²
Cercle
π × Rayon²
Parallélograme
Base × Hauteur
Exemple : Un terrain de football rectangulaire de 100 m sur 60 m a une aire de 100 × 60 = 6 000 m².
Vous devez peindre un mur de votre chambre. Pour savoir quelle quantité de peinture acheter, vous calculez l'aire du mur. Si votre mur mesure 4 m de long et 2,5 m de haut, son aire est de 10 m². La notice indique qu'un pot couvre 5 m², vous en aurez donc besoin de deux.
L'aire se distingue du périmètre qui mesure seulement le contour. Une figure peut avoir un grand périmètre mais une petite aire, et inversement.
N°50 - Périmètre
Le périmètre est la longueur totale du contour d'une figure géométrique plane. Il se mesure en unités de longueur (cm, m, km).
Formules principales :
Rectangle
2 × (Longueur + Largeur)
Carré
4 × Côté
Triangle
Côté 1 + Côté 2 + Côté 3
Cercle (circonférence)
2 × π × Rayon
Exemple : Un jardin carré dont chaque côté mesure 8 m a un périmètre de 4 × 8 = 32 m.
Vous voulez installer une clôture autour de votre jardin. Pour savoir combien de mètres de grillage acheter, vous calculez le périmètre. Si votre jardin rectangulaire fait 15 m sur 10 m, le périmètre est 2 × (15 + 10) = 50 m de clôture nécessaire.
Le périmètre, c'est le chemin que vous parcourez si vous faites le tour complet d'une figure en marchant sur ses bords. L'aire, c'est ce qu'il y a à l'intérieur.
Le vocabulaire mathématique en statistiques et probabilités
Voici enfin quelques définitions importantes en statistiques et probabilités4.
N°51 - Calcul statistique
Les calculs statistiques regroupent l'ensemble des méthodes mathématiques permettant de collecter, organiser, analyser et interpréter des données numériques. Ils transforment des informations brutes en résultats exploitables :
Moyenne
Valeur centrale d'une série
Médiane
Valeur qui partage les données en deux groupes égaux
Ecart type
Mesure de dispersion
Variance
Carré de l'écart type
Quartiles
Division en quatre parties égales
Exemple : Un professeur calcule la moyenne de classe : (12 + 15 + 8 + 14 + 11) ÷ 5 = 12/20. Il peut aussi calculer l'écart type pour savoir si les notes sont homogènes ou dispersées.
Suivez vos dépenses mensuelles. Les calculs statistiques vous permettent de connaître votre dépense moyenne, d'identifier les mois où vous avez le plus dépensé (maximum), et de voir si vos dépenses sont régulières ou variables (écart type).
Les calculs statistiques sont partout : sondages d'opinion, analyses de performances sportives, études de marché, prévisions météorologiques, ou encore algorithmes de recommandation sur Netflix et Spotify.
N°52 - Corrélation
La corrélation mesure l'intensité et le sens de la relation entre deux variables. Elle indique si deux phénomènes évoluent ensemble, sans nécessairement prouver un lien de cause à effet.
Types de corrélation :
Positive
Les deux variables augmentent ensemble (coefficient entre 0 et +1)
Négative
Quand l'une augmente, l'autre diminue (coefficient entre -1 et 0)
Nulle
Aucune relation détectable (coefficient proche de 0)
Exemple : En analysant 100 élèves, on observe que ceux qui passent plus d'heures à réviser obtiennent généralement de meilleures notes. La corrélation est positive (environ +0,7), ce qui est considéré comme fort.
Plus vous pratiquez un instrument de musique, meilleur vous devenez : c'est une corrélation positive. À l'inverse, plus vous passez de temps sur les réseaux sociaux, moins vous avez de temps pour étudier : corrélation négative.
Corrélation ne signifie pas causalité ! Exemple célèbre : il existe une corrélation entre les ventes de glaces et les noyades. Mais manger des glaces ne provoque pas de noyades ; c'est simplement que les deux augmentent en été (variable cachée : la température).
Prenez des cours de maths pour mieux comprendre !
N°53 - Écart type
L'écart type (symbole σ, sigma) mesure la dispersion des valeurs d'une série par rapport à leur moyenne. Plus l'écart type est élevé, plus les données sont dispersées ; plus il est faible, plus elles sont concentrées autour de la moyenne.
Formule simplifiée : √(Somme des (valeur - moyenne)² ÷ effectif)
Exemple : Deux classes ont une moyenne de 12/20.
- Classe A : notes entre 11 et 13 → écart type faible (0,8)
- Classe B : notes entre 4 et 20 → écart type élevé (4,5)
L'écart type révèle que la classe A est homogène, tandis que la classe B est très hétérogène.
Admettons que vous compariez deux trajets domicile-travail. Le trajet A prend toujours entre 28 et 32 minutes (moyenne 30 min, faible écart type = prévisible). Le trajet B prend entre 15 et 60 minutes selon le trafic (moyenne 30 min aussi, mais fort écart type = imprévisible).
En finance, l'écart type mesure la volatilité d'un placement : un faible écart type indique un investissement stable, un fort écart type signale un risque élevé mais potentiellement plus rentable.
N°54 - Intervalle de confiance
L'intervalle de confiance est une fourchette de valeurs dans laquelle se situe probablement la vraie valeur d'un paramètre, avec un certain niveau de certitude (généralement 95 % ou 99 %).
Structure : [Valeur estimée - marge d'erreur ; Valeur estimée + marge d'erreur]
Exemple : Un sondage indique que 52 % des Français préfèrent les vacances à la mer, avec un intervalle de confiance à 95 % de [49 % ; 55 %]. Cela signifie qu'on est sûr à 95 % que le vrai pourcentage se situe dans cette fourchette.
Votre GPS annonce une arrivée prévue à 15h20, avec une marge d'incertitude de ±10 minutes. L'intervalle de confiance est donc [15h10 ; 15h30]. Plus le trafic est prévisible, plus l'intervalle sera étroit.
Facteurs influents :
Taille de l'échantillon
Plus l'échantillon est grand, plus l'intervalle est étroit
Niveau de confiance
Viser 99 % au lieu de 95 % élargit l'intervalle
Variabilité des données
Des données très dispersées élargissent l'intervalle
Un médicament réduit la fièvre de 1,8°C en moyenne, avec un intervalle de confiance à 95 % de [1,5°C ; 2,1°C]. On est donc très confiant dans son efficacité.
N°55 - Médiane
La médiane est la valeur centrale d'une série de données ordonnées par ordre croissant. Elle partage la série en deux groupes égaux : 50 % des valeurs sont inférieures, 50 % sont supérieures.
Méthode de calcul :
Effectif impair : la médiane est la valeur du milieu
Effectif pair : la médiane est la moyenne des deux valeurs centrales
Exemple : Soit une série de salaires : 1 500 € - 1 600 € - 1 800 € - 2 000 € - 5 000 €. La médiane est 1 800 € car c'est la valeur centrale.
Imaginez une file de 5 personnes classées par taille : 1,50 m - 1,65 m - 1,70 m - 1,75 m - 1,95 m. La personne du milieu (1,70 m) représente la médiane. Même si quelqu'un de 2,20 m remplace la dernière personne, la médiane reste 1,70 m.
La médiane est insensible aux valeurs extrêmes. C'est pourquoi on l'utilise pour les salaires (une minorité de très hauts salaires fausse la moyenne) ou les prix immobiliers.
N°56 - Moyenne arithmétique
La moyenne arithmétique (ou simplement "moyenne") est la somme de toutes les valeurs divisée par leur nombre total (effectif). C'est l'indicateur statistique le plus utilisé.
Formule : Moyenne = (x₁ + x₂ + ... + xₙ) ÷ n
Exemple : Soient les notes d'un élève : 12, 15, 8, 14, 11. La moyenne est (12 + 15 + 8 + 14 + 11) ÷ 5 = 60 ÷ 5 = 12/20
Vous avez dépensé en courses : 45 €, 62 €, 38 €, 55 € sur quatre semaines. Votre dépense moyenne hebdomadaire est (45 + 62 + 38 + 55) ÷ 4 = 50 €/semaine. Cela vous aide à prévoir votre budget.
Dans certains cas, toutes les valeurs n'ont pas le même poids. Par exemple, un devoir noté sur 20 avec coefficient 2 compte double. C'est ce qu'on appelle la moyenne pondérée :
- Devoir 1 (coef 1) : 14/20
- Devoir 2 (coef 2) : 16/20
- Moyenne pondérée = (14×1 + 16×2) ÷ (1+2) = 46 ÷ 3 = 15,33/20
La moyenne peut être trompeuse en présence de valeurs extrêmes. Exemple : dans une entreprise de 10 personnes, 9 gagnent 1 500 € et le PDG 20 000 €. La moyenne est 3 350 €, ce qui ne représente la réalité de personne !
N°57 - Pourcentage
Le pourcentage exprime une proportion ou une partie d'un tout rapportée à 100. Le symbole % signifie "pour cent" ou "sur 100".
Formules essentielles :
Calculer un pourcentage
(Partie ÷ Total) × 100
Calculer une valeur
(Pourcentage ÷ 100) × Total
Calculer une augmentation
Valeur initiale × (1 + pourcentage/100)
Calculer une réduction
Valeur initiale × (1 - pourcentage/100)
Exemple : Dans une classe de 25 élèves, 15 sont des filles. Le pourcentage de filles est (15 ÷ 25) × 100 = 60 %.
Vous voyez un pull à 80 € soldé -30 %. La réduction en euros est de 80 × 0,30 = 24 €. Le prix final sera de 80 - 24 = 56 € (ou directement : 80 × 0,70 = 56 €).
Une augmentation de 20 % suivie d'une baisse de 20 % ne ramène PAS au prix initial ! 100 € + 20 % = 120 €. 120 € - 20 % = 120 x 0,80 = 96 € (et non 100).
N°58 - Mode
Le mode (ou valeur modale) est la valeur qui apparaît le plus fréquemment dans une série statistique. Une série peut avoir un seul mode (unimodale), plusieurs modes (multimodale), ou aucun mode si toutes les valeurs apparaissent le même nombre de fois.
Exemple : Soient les pointures dans un groupe : 38, 39, 39, 40, 39, 41, 42, 39. Le mode est 39 (apparaît 4 fois).
Soient les notes d'un élève : 8, 10, 10, 10, 12, 14, 14, 14, 16. Les modes sont 10 et 14 (apparaissent chacun 3 fois).
Dans votre garde-robe, vous avez 3 chemises bleues, 5 chemises blanches, 2 chemises noires et 1 chemise rouge. Le mode est blanc car c'est la couleur la plus fréquente. Cela peut vous aider à décider quelle couleur ne plus acheter !
Un magasin de chaussures constate que la pointure modale chez les hommes est 42. Il commandera donc plus de paires en cette taille pour éviter les ruptures de stock.
N°59 - Tableau de fréquence
Le tableau de fréquence est un outil d'organisation qui présente les valeurs d'une série accompagnées de leur effectif (nombre d'apparitions) et de leur fréquence (proportion par rapport au total).
La structure type :
| Valeur | Effectif | Fréquence | Fréquence % |
|---|---|---|---|
| A | 5 | 5/20 = 0,25 | 25 % |
| B | 8 | 8/20 = 0,40 | 40 % |
| C | 7 | 7/20 = 0,35 | 35 % |
| Total | 20 | 1 | 100 % |
Exemple avec les notes obtenues lors d'un contrôle (sur 10 élèves) :
| Note | Effectif | Fréquence |
|---|---|---|
| 8 | 2 | 20 % |
| 10 | 3 | 30 % |
| 12 | 1 | 10 % |
| 14 | 4 | 40 % |
Vous suivez vos moyens de transport pendant un mois (20 jours travaillés) :
- Voiture : 12 jours (60 %)
- Vélo : 5 jours (25 %)
- Transports en commun : 3 jours (15 %)
Ce tableau vous montre clairement vos habitudes.
Additionnez progressivement les fréquences. Utile pour répondre à "Combien d'élèves ont eu au moins 12 ?" ou "Quel pourcentage gagne moins de 2 000 € ?"
N°60 - Expérience aléatoire
Une expérience aléatoire est une expérience dont on ne peut pas prédire avec certitude le résultat, même si on connaît toutes les conditions initiales. Chaque résultat possible est appelé une issue, et l'ensemble de toutes les issues forme l'univers des possibles.
Les caractéristiques de l'expérience aléatoire :
Reproductibilité
On peut la répéter dans les mêmes conditions
Résultats connus
On connaît tous les résultats possibles
Incertitude
On ne peut pas prédire quel résultat se produira
Exemples classiques :
- Lancer un dé : univers = {1, 2, 3, 4, 5, 6}
- Tirer une carte : univers = 52 cartes
- Pile ou face : univers = {Pile, Face}
- Tirage du Loto : combinaisons possibles
Vous tirez un vêtement au hasard dans votre armoire sans regarder. Vous savez ce qu'elle contient (3 t-shirts bleus, 2 rouges, 1 vert), mais vous ne pouvez pas prédire la couleur que vous allez sortir. C'est une expérience aléatoire.
En médecine, tester l'efficacité d'un médicament est une expérience aléatoire : on connaît les résultats possibles (guérison, amélioration, pas d'effet, effets secondaires), mais on ne peut pas prédire avec certitude ce qui arrivera à chaque patient.
Plus on répète une expérience aléatoire, plus la fréquence observée se rapproche de la probabilité théorique. Si vous lancez 10 fois une pièce, vous pouvez obtenir 7 fois pile. Mais si vous la lancez 10 000 fois, vous obtiendrez environ 50% de pile.
Pour celles et ceux qui ont des questions : ne pas hésiter à demander de l'aide au professeur de mathématiques lors des cours particuliers à domicile de maths.
De l'algèbre à la géométrie, en passant par les statistiques et les probabilités, ce vocabulaire mathématique forme la colonne vertébrale de toutes les disciplines scientifiques et techniques. Comprendre ces termes, c'est se donner les moyens de :
🧮 Résoudre des problèmes du quotidien (calculer une surface, interpréter des statistiques, comprendre un pourcentage)
📈 Progresser dans ses études, du collège jusqu'aux formations supérieures
🧠 Développer son esprit logique et sa capacité d'analyse
🗣️ Communiquer efficacement dans un contexte scientifique ou professionnel
Sources
- "Résultats des élèves : la France et le classement PISA 2022." Vie Publique, Direction de l'information légale et administrative, 5 déc. 2023. Disponible à www.vie-publique.fr/eclairage/19539-resultats-des-eleves-la-france-et-le-classement-pisa-2022. Consulté le 28 janvier 2026
- Baruk, Stella. Dictionnaire de mathématiques élémentaires. Seuil, 1992.
- Deledicq, André, et Jean-Christophe Deledicq. Le Monde des nombres. Éditions Pole, 2008. Disponible à https://archive.org/details/lemondedeschiffr0000dele. Consulté le 30 janvier 2026
- Vermeil, Jean. Statistiques : Probabilités, Estimation, Tests. Vuibert, 2005.
Résumer via IA :
















Un superbel liste pour les étudiants de FLE
Bonjour monsieur
Ma fille qui est en troisième a un problème à résoudre . Savez vous ce que l’on peut penser de cette définition : »le nombre de moitiés dans un tout »
Merci d’avance
Bonjour, en toute logique, une moitié donne un tout si on la multiplie par deux. Il y a donc deux moitiés pour faire un tout.
Bonne journée.
« (n+1)/2 = 1 500″ !!!!!
» (x1 + x2 + x3 + xi) / n »
c’est faux!
Vous êtes sérieux!!!
MERCI BEAUCOUP POUR CETTE FORMATION C’EST SUFFISANTES POUR D’ÊTRE AU COURANT AVEC LES COURS
Bonjour
Et que veux dire « deux à deux «
Exemple – si 2 triangle ont un côté de même longueur compris entre 2 triangle deux à deux de même mesure…..
Bonjour,
Le terme deux à deux signifie que l’on parle d’une relation binaire. Autrement dit, pourrait remplacer deux à deux par « tous les deux ».
Bien à vous
Excellent !
Merci pour tout
A toi aussi
Merci
Ce je demande sa vous dire quoi à travers an mathe
rien a pars refléchir
Pas claire ni explicite.purement répétitif.
Bonjour,
Merci pour votre retour ! Nous sommes désolés si l’article ne vous a pas semblé clair ou assez détaillé. Votre avis est précieux, et nous allons revoir le contenu pour le rendre plus explicite et moins répétitif. N’hésitez pas à nous dire ce que vous aimeriez voir dans un article sur ce sujet, cela nous aidera à l’améliorer.